基于二阶和高阶统计量DOA估计算法的对比＊

廖春艳

(湖南科技学院数学与计算科学系，湖南永州 425100)

基于二阶和高阶统计量DOA估计算法的对比＊

廖春艳

(湖南科技学院数学与计算科学系，湖南永州 425100)

阵列信号处理是信号处理的一个重要分支，而波达方向估计又是阵列信号处理的一个重要方面，一些常用的方法可以用来获得DOA估计，例如基于二阶统计量的MUSIC法，但是这些方法存在一些缺点.对比了基于二阶和高阶统计量的DOA估计算法性能，仿真结果表明，基于高阶统计量的DOA估计算法具有更好的性能，此外，还分析了基于二阶或高阶统计量的DOA估计算法的相同点和不同点.

阵列信号处理;DOA估计;MUSIC算法;二阶统计量;高阶统计量

作为信号处理的一个重要分支，阵列信号处理广泛应用在雷达、声纳、地震信息、无线通信、生物医学工程等多个军事和民用领域［1－4］.

阵列信号处理是利用阵列天线对信号进行空间采样并进行处理，阵列信号处理的主要问题包括:波束形成技术——使阵列方向图的主瓣指向所需的方向;零点形成技术——使天线的零点对准干扰方向;空间谱估计——对空间信号波达方向的分布进行超分辨率估计.利用阵列信号处理技术实现对远场信号的波达方向(DOA－direction of arrival)进行估计是阵列信号空间谱估计研究的主要内容.波达方向的估计方法大致可分为两大类:一类是参数化的方法，另外一类是基于空间谱的方法.参数化的方法通常要求同时对所有感兴趣的参数进行搜索，如极大似然法，这就会使计算量大大增加.空间谱分析方法是指构造一个以空间方位为参数的谱函数，其典型的算法是MUSIC算法，基于接收信号相关矩阵特征值分解的MUSIC算法具有良好的DOA估计性能，它是利用信号子空间和噪声子空间的正交性，构造空间谱函数，通过谱峰搜索来检测信号的DOA［5］.

长期以来，在阵列信号处理中人们习惯于假设信号或噪声服从高斯分布.这样，仅用二阶统计量或基于二阶统计量的功率谱分析便可以提取信息，进行各种处理.但在许多实际过程中产生的信号往往是非高斯分布的，非高斯信号是一种更为普遍的信号，过去由于缺乏必要的分析工具，人们也只能将这些信号近似假定为高斯信号进行处理.随着信息科学的迅猛发展，将高阶统计量应用于阵列信号处理已经取得了很大的发展，在阵列信号处理中使用高阶统计量有几个好处:1)当加性噪声是高斯有色噪声时，基于二阶统计量的高分辨DOA算法(例如MUSIC法)工作得不好，而基于累积量的MUSIC算法却能工作得很好;2)高阶统计量不仅可以消除加性高斯噪声的影响，而且还可以消除加性非高斯噪声的影响.

1 高阶统计量的基本概念［5］

1.1 随机变量的特征函数

对于概率密度为f(x)的随机变量x，其第一特征函数为:

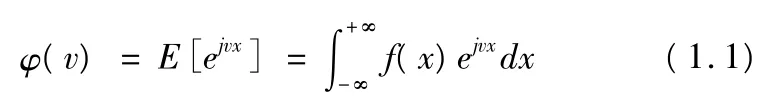
其第二特征函数为:

1.2 随机变量的k阶矩和k阶累量

k 阶矩为:

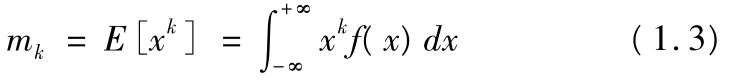
k阶累量为:

1.3 随机向量的r阶矩和r阶累量

r阶矩:

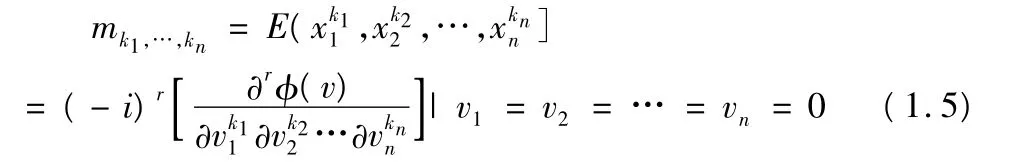
r阶累量:

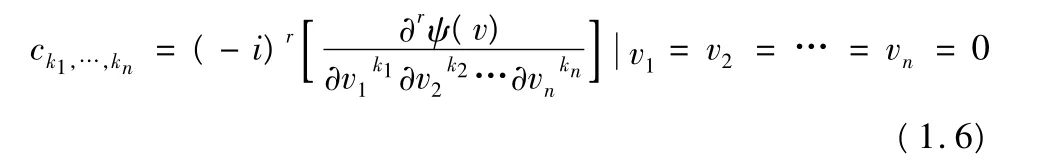
1.4 随机过程的r阶矩和r阶累量

1.5 高阶谱的定义

将随机过程{x(n)}的k阶累量的(k－1)维傅里叶变换定义为{x(n)}的k阶谱.之所以用k阶累量而不是k阶矩来定义k阶谱的原因在于:

(1)高阶累量的使用可以避免高斯有色噪声的影响，而高阶矩却不能;

(2)两个统计独立的随机过程之和的累量等于各个随机过程的累量之和，这样在实际处理加性信号时将带来运算上的方便，而高阶矩却不满足此性质;

(3)独立同分布过程的高阶累量为δ函数，因而其傅里叶变换是多维平坦的.

2 基于高阶统计量的波达方向估计算法推导［6］

用四阶累积量做研究，设第m个阵元的输出信号为:

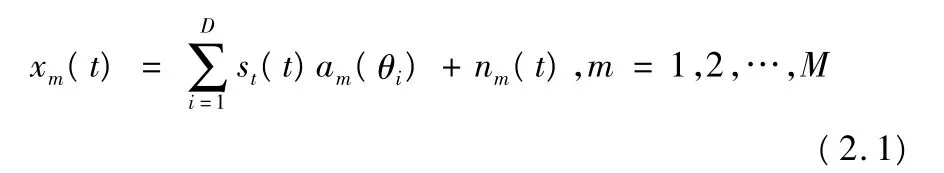
矩阵形式如下:X=AS+N

输出信号的四阶累积量矩阵为:

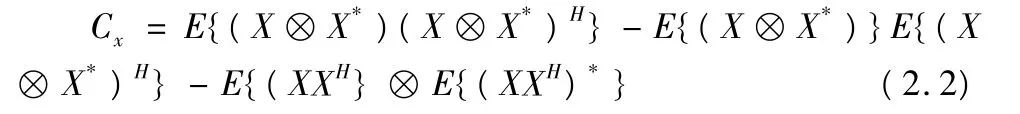
将X=AS+N代入式2.2得:

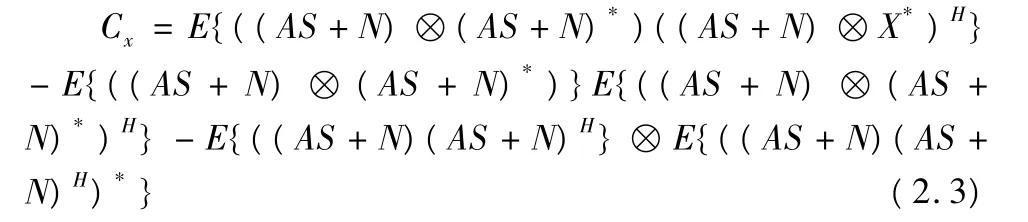
根据Kronecker乘积的性质，得:

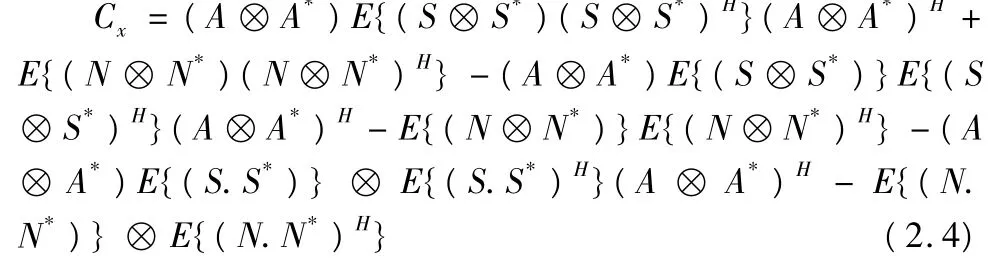
令:R=A⊗A*

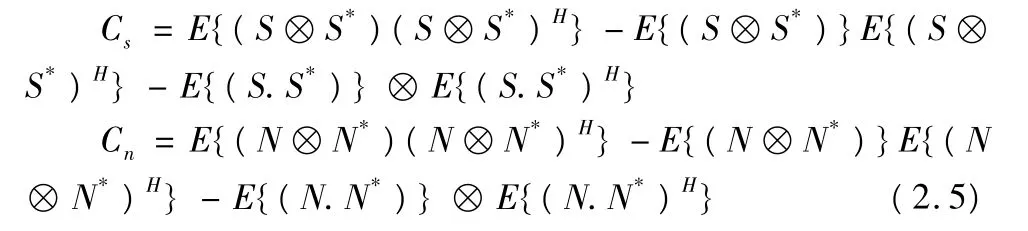
Cs和Cn分别为信源和噪声的空间四阶累积量矩阵，这样式2.2 可以写成

对 Cx进行特征分解，其特征值从大到小排列为 λ1，λ2，…，λM2，设对应的特征向量为 μ1，μ2，…，μM2.由于 rank(RCsRH)=D2，所以Cx应有D2个大的特征值和M2－D2个小特征值，小特征值对应的特征向量张成的空间定义为噪声子空间，即:

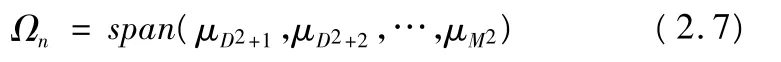
同时定义信号子空间为:

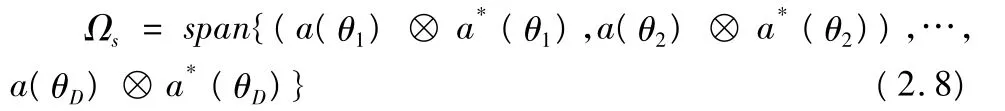
得到正交条件:

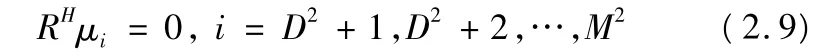
定义噪声矩阵En:

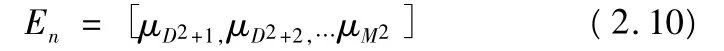
基于四阶累积量矩阵的空间谱定义为:

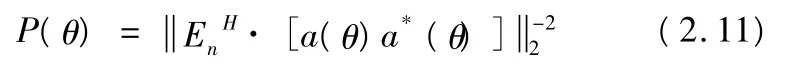
由于在辐射源方向上具有正交方程，在该方向上的谱值取得极大值.

3 基于高阶统计量的波达方向估计步骤

a)根据各阵元收到的信号构造复解析形式，从而得到矩阵X;

b)求矩阵的四阶累积量矩阵Cx;

c)对Cx进行特征分解，计算四阶累积量的空间谱;

d)搜索谱峰就可以得到信源方向.

4 基于高阶统计量DOA估计仿真分析

仿真条件:阵元数为6，SNR=10，阵元间距为0.2波长，2 个信号源，入射角为10°，60°.结果见图1、图2.

图1 d＜时，基于二阶统计量的DOA估计

图2 d＜时，基于高阶统计量的DOA估计

仿真条件:阵元数为6，SNR=10，阵元间距为0.5波长，2 个信号源，入射角为 10°，60°.结果见图 3、图 4.

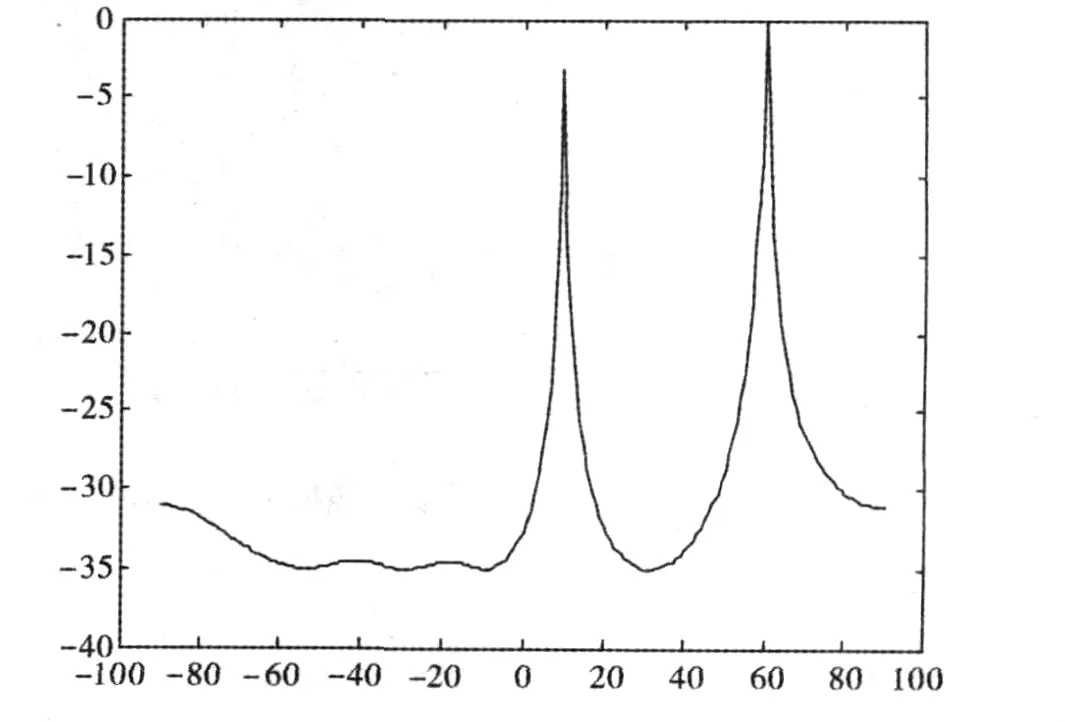
图3 d=时，基于二阶统计量的DOA估计

仿真条件:阵元数为6，SNR=10，阵元间距为0.6波长，2 个信号源，入射角为 10°，60°.结果见图 5、图 6.

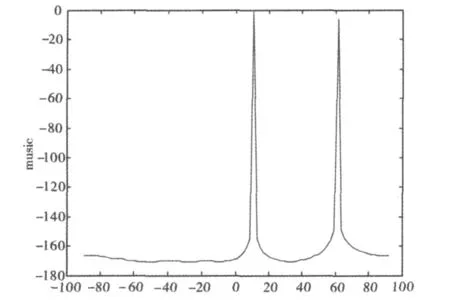
图4 d=时，基于高阶统计量的DOA估计

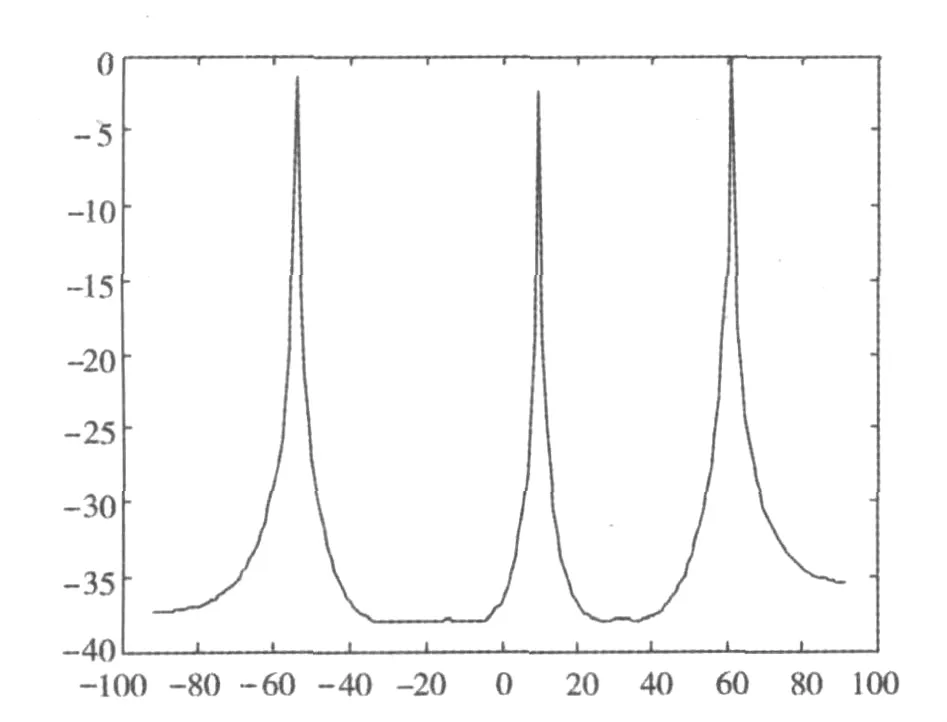
图5 d＞ 时，基于二阶统计量的DOA估计

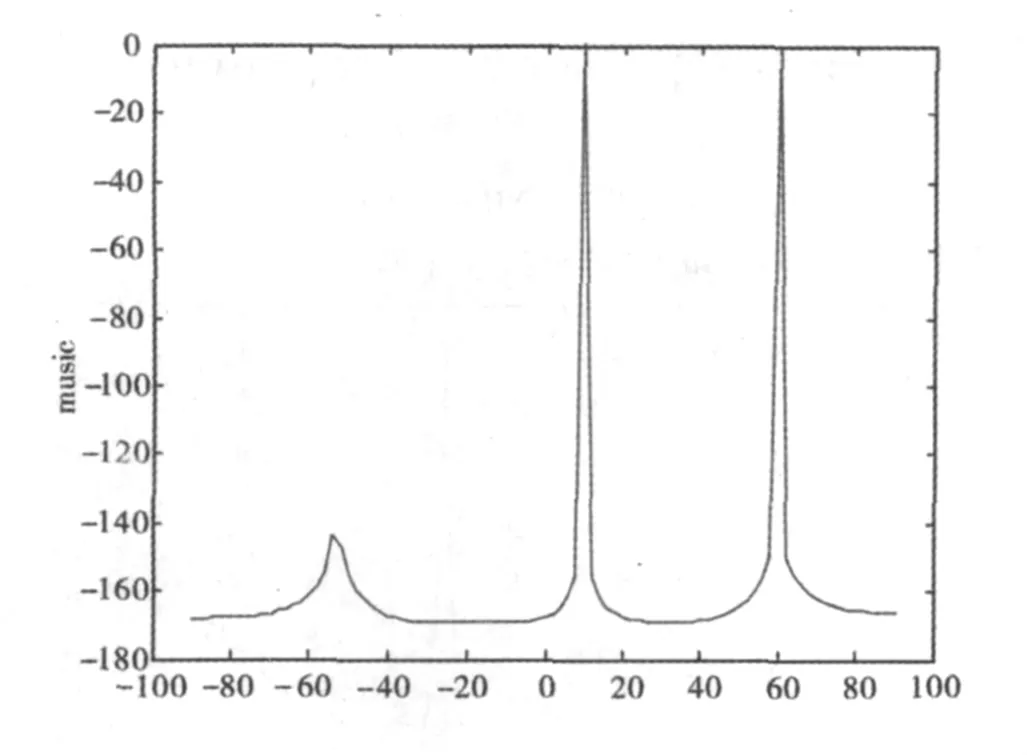
图6 d＞ 时，基于高阶统计量的DOA估计

5 结论

从仿真结果可以看出基于高阶统计量的DOA估计与基于二阶统计量的DOA估计的相同点和不同点:

不同点:同样是利用特征分解法，基于高阶累积量的MUSIC显示了很好的抗干扰能力，在相同信噪比条件下，基于高阶累积量的MUSIC方法明显优于基于二阶统计量的MUSIC算法，在时，可以很清楚地看到基于高阶累量得到的谱峰比基于二阶统计量得到的谱峰更加明显.在d＞时，虽然两者都出现了栅瓣，但是从图5、图6可以看出，基于高阶累量的栅瓣部分的谱峰明显得到抑制，这是由于此仿真用的是高斯白噪声，高斯信号3阶以上的累量恒为0，所以即使阵元之间的间隔不满足出现栅瓣部分的谱峰也得到了明显抑制.

总之，用基于高阶统计量的MUSIC算法估计波达方向能够有效地抑制高斯白噪声甚至高斯色噪声的影响，估计性能在很大程度上优于传统的基于二阶统计量所得到的DOA估计.

［1］张贤达，保铮.通信信号处理［M］.北京:国防工业出版社，2000.

［2］Manolakis D G，lngle V K，Kogon S M.统计与自适应信号处理［M］.周正，顾仲梅，译.北京:电子工业出版社，2003.

［3］刘刚，吕新华，攸阳.阵列信号处理中基于MUSIC算法的空间谱估计［J］.微计算机信息，2006，(12):302 －303.

［4］冯亚俊.基于 MUSIC算法的 DOA估计［J］.信息科学，2007，(10):1606－1609.

［5］葛哲学，陈仲生.Matlab时频分析技术及其应用［M］.北京:人民邮电出版社，2006.

［6］梁清泉，程刚.基于高阶统计量的波达方向估计技术的研究［D］.西安:西北工业大学硕士学位论文，2002.

O213.2

A

1008－4681(2012)02－0018－03

2012－02－11

湖南科技学院2010年校级课题(批准号:10XKYTC029).

廖春艳(1984－)，女，江西吉安人，湖南科技学院数学与计算科学系助教，硕士.研究方向:基础数学.

(责任编校:晴川)