主动防御协同自适应滑模制导律

花文华, 陈兴林, 宋超

(1.洛阳光电技术发展中心 控制系统研究所，河南 洛阳 471009;2.哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001;3.天津航海仪器研究所 第十研究室, 天津 300131)

主动防御协同自适应滑模制导律

花文华1,2, 陈兴林2, 宋超3

(1.洛阳光电技术发展中心 控制系统研究所，河南 洛阳 471009;2.哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001;3.天津航海仪器研究所 第十研究室, 天津 300131)

飞机相比于攻击导弹,在飞行速度和机动性能等方面存在着劣势。为了提高其生存几率,设计了一种发射防御导弹协同对抗攻击导弹的自适应滑模制导律。该制导律本质是一种视线(Line of Sight, LOS)制导方法,通过对飞机与防御导弹和防御导弹与攻击导弹间的LOS调整以满足特定的几何关系,从而实现对攻击导弹的主动防御。最后,将所设计的制导律与比例导引进行了仿真比较。结果表明,由于与目标间的协同,所设计的制导律在机动性能和拦截性能方面具有明显的优势,且对于三方的飞行速度变化与攻击导弹的机动具有较强的鲁棒性。

制导律; 自适应滑模控制; 协同; 视线制导

引言

相比于攻击导弹,飞机在飞行速度和机动性能等方面存在较大的劣势,为规避威胁往往采用一些较为被动的防御措施,如投放箔条弹等,但即使具有足够的飞行速度和机动性能,也可能因为负载约束或任务目标,如要求按照规划航路到达指定区域、载有大型侦察天线或者运送伤员等而无法规避机动,因此发射防御导弹进行主动防御是一种可选的方式。

对于主动防御的三方——飞机(Target)、防御导弹(Defender)和攻击导弹(Missile)制导情形,文献[1]首先分析了最优制导策略的可行性,文献[2]假设防御方非机动,攻击导弹与防御导弹具有理想自动驾驶仪动态且无机动界约束,推导了三方的闭环运动学关系。文献[3]将该情形定义为连续微分对策问题,采用冲激函数以获得相应Riccati微分方程的离散解,而文献[4]则直接将情形定义为离散对策问题。文献[5]在非完全信息(Imperfect Information)[6-7]情形下,假设攻击导弹制导策略为比例导引、扩展比例导引或最优制导律中的一种,研究了一种基于多模型自适应估计与控制的自适应制导方法。上述方法都完全或部分基于线性化假设,具有一定的局限性。文献[8]给出了一种视线(Line of Sight, LOS)制导[9-10]方法,并在防御方机动的情形下,分析了三方的运动学关系,但该方法是一种几何方法,对于系统内部的不确定性不具有鲁棒性。本文针对飞机与防御导弹协同对抗攻击导弹这一问题,给出一种协同自适应滑模制导律,这一方法本质是一种LOS制导方法,但是由于采用自适应滑模的设计思路,对于系统内部的不确定性和外部干扰具有较强的鲁棒性。

1 问题的数学描述

飞机、防御导弹和攻击导弹三方的平面相对运动关系如图1所示,下标t,d和m表示其相关状态,其中a,v,γ,λ和R分别表示加速度、飞行速度、航向角、视线角和相对距离。结合图1,三方的相对运动关系可表示为:

(1)

(2)

(3)

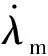
(4)

(5)

(6)

式中,vm,vt和vd满足vm,vd>vt,目标具有速度上的劣势。

图1 三方平面相对运动关系

假设三方具有理想自动驾驶仪动态或机动动态(Maneuvering Dynamics),且机动有界

(7)

|ai|≤ai,max

(8)

式中,at,max,ad,max和am,max满足am,max,ad,max>at,max,目标具有机动性能上的劣势。

对式(5)和式(6)两边求导,可以得到:

(9)

(atcos (γt-λd)-Δd)

(10)

其中:

amcos (γm-λdm)

(11)

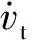
(12)

式中,Δdm为防御导弹与攻击导弹的径向加速度和攻击导弹的法向加速度在二者LOS法向上的分量;Δd为目标与防御导弹的径向加速度在二者LOS法向上的分量。假设Δdm和Δd有界,当作干扰或不确定项处理:

|Δdm|≤Δ1

(13)

|Δd|≤Δ2

(14)

式中,Δi(i=1,2)未知。

2 协同滑模制导律推导

图2为LOS制导期望的相对运动关系,防御导弹位于目标与攻击导弹间的视线上,满足

λm=λd=λdm=λ

(15)

使得目标与防御导弹和防御导弹与攻击导弹间的视线方向保持一致,从而随着防御导弹与攻击导弹的不断接近,实现对目标的保护。假设攻击导弹可以对目标进行相关的量测和跟踪,但无法获取防御导弹的相关信息,这一假设符合实际,因为大多数的导弹只能够对所跟踪的单一目标进行拦截[5]。

图2 三方平面LOS关系

基于LOS制导思想,结合图1和图2,取偏差σ=λdm-λd,则定义滑模面为:

(16)

由上式可得:

σ=σ0exp(-(t-t0)/ε)

(17)

(18)

其中:

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

自适应律:

(28)

(29)

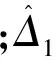
(30)

式中,κ为常数。

式(30)的含义为随着防御导弹和攻击导弹的不断接近,对趋近于滑模面的速度进行调整,特别是当Rdm接近0时,可以避免视线角速度的发散,在一定程度上也可以缓解抖振。仿真中采用饱和函数近似代替符号函数,以进一步削弱抖振的影响。

稳定性分析:

定义Lyapunov函数

(31)

其中:

(32)

则:

=s(-ks-ηsgn (s)+α5Δm+α6Δd)-

≤-ks2-η|s|+α5|s|Δ1+α6|s|Δ2-

=-ks2

(33)

(34)

考虑机动有界,式(18)进一步修正为:

(35)

由式(35)可知,为实现防御导弹与目标之间的协同,前者所需的信息包括目标的加速度at、飞行速度Vt和航向角γt,以及二者之间的相对运动信息。控制命令的计算具有两种可行方式:第一种为目标和防御导弹将相关信息传输给一个集中协调单元,如制导站等进行计算,并通过指令传输通道将控制命令传输到防御导弹上;第二种方式为目标通过(单向)数据链或其它方式将相关信息直接传输给防御导弹,采用弹上计算的方式进行控制命令的计算。前一种方式类似于指令制导,而后一种方式实时性更高,对于信息传输方式的具体实现,仍需要进一步的研究。

3 仿真结果及分析

下面主要针对非机动目标和“Bang-Bang”机动目标的保护进行仿真研究。目标发射防御导弹,假设其初始位置为(xt=0,yt=0);攻击导弹的初始位置为(xm=3 000 m,ym=4 000 m);三方的飞行速度分别为vt=300 m/s,vd=500 m/s,vm=500 m/s;γt=0°,γd=40°,γm=225°,γ1=γ2=0.1;ε=0.2;κ=4。仿真中假设攻击导弹采用比例导引(Proportional Navigation, PN),机动无约束,目标和防御导弹机动有界,at,max=5g,ad,max∈{10g,15g}。

(1)目标非机动

假设目标非机动且保持当前航向飞行,此时若采用PN拦截目标则是最优的[11],取ad,max=15g,仿真结果如图3～图6所示。其中,图3和图4为防御导弹分别采用所设计的协同自适应滑模制导律CASD和PN制导律的三方飞行弹道。从图中可以看出,两种制导方法都可以实现对攻击导弹的有效拦截,图3中的目标与防御导弹和防御导弹与攻击导弹间的视线逐渐趋于一致,最终的脱靶量分别为0.093 m和0.803 m,CASD性能较好。图5为两种制导方法的加速度变化曲线。由图可见,CASD在初始阶段以最大加速度运行以实现对飞行弹道的调整,由于与目标之间的协同,在约1.2 s后的加速度小于PN,整体性能优于PN。图6为CASD的误差角,由图可知,σ趋于0。

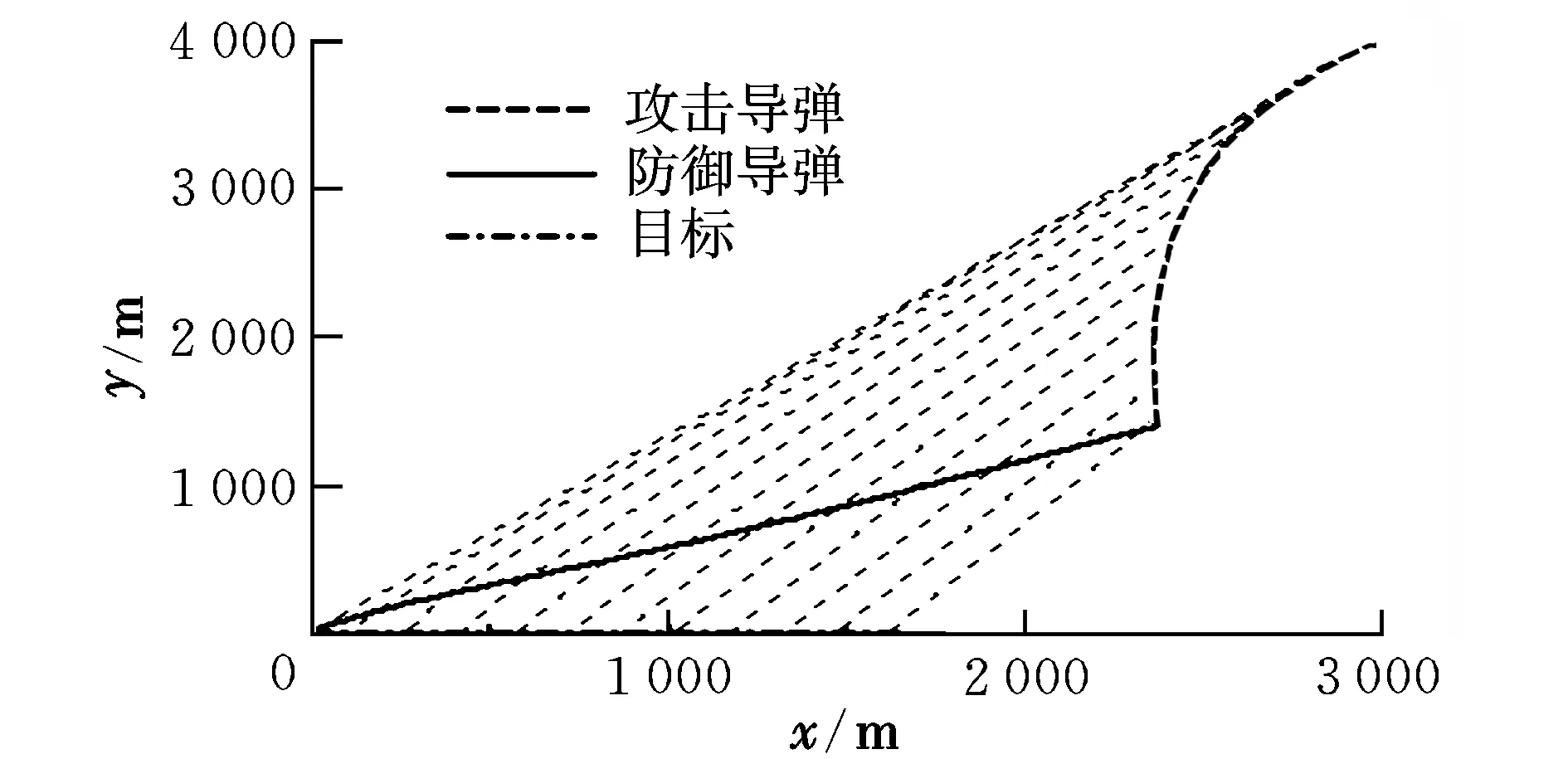
图3 飞行弹道(CASD)

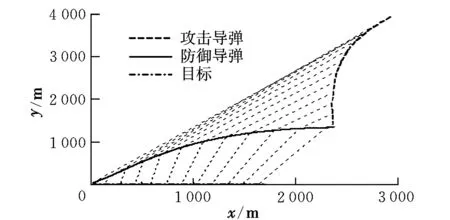
图4 飞行弹道(PN)

图5 防御导弹的加速度

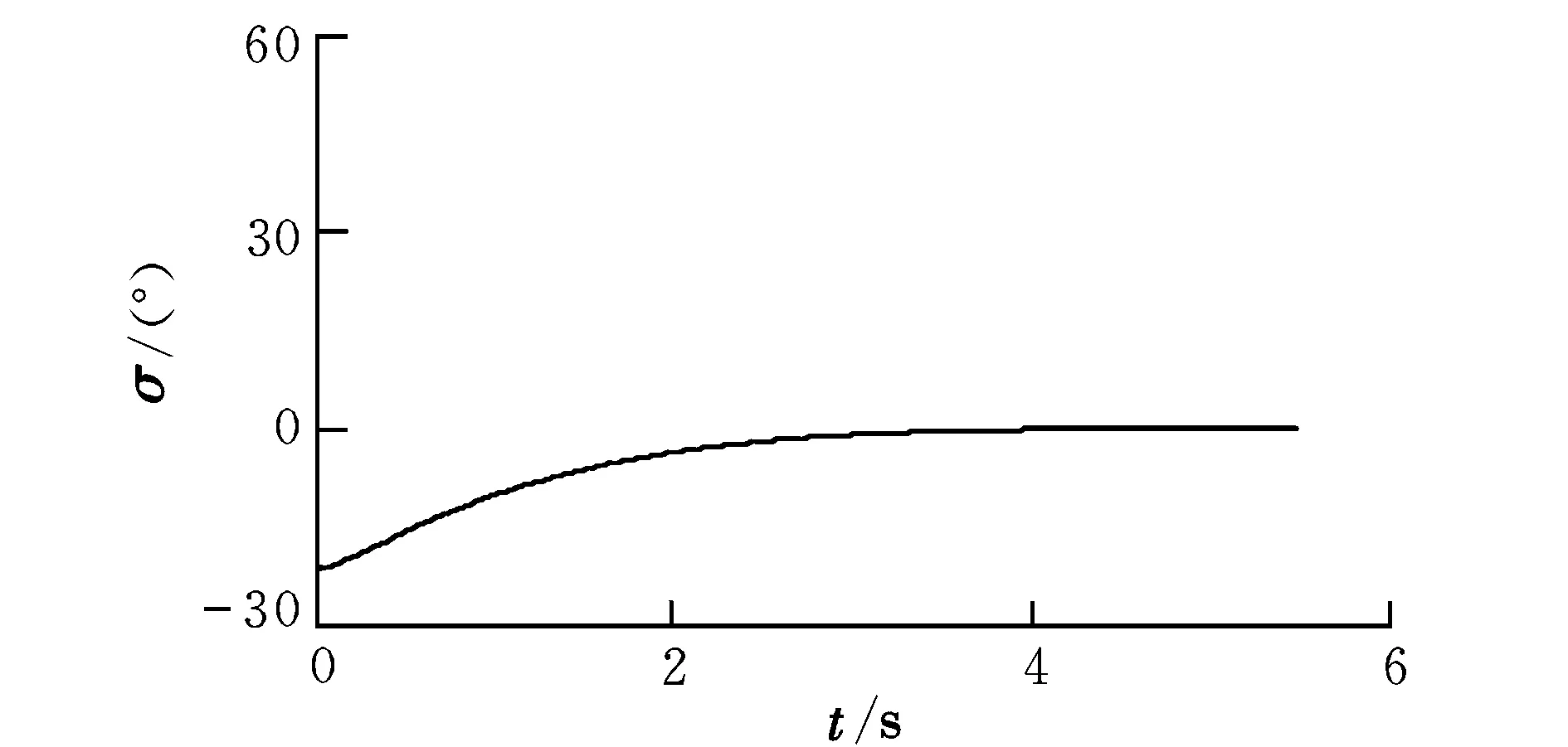
图6 误差角(CASD)

图7为取ad,max=10g情形下两种制导律的加速度变化曲线。由图可见,PN在约2.3 s后发生了严重的执行饱和,从而使最终的脱靶量高达12.9 m,而CASD仅为0.096 m,可见CASD具有明显的机动性能优势。

图7 防御导弹的加速度

(2)目标“Bang-Bang”机动

该类型的机动是最优的规避机动[12],假设目标只具有一次机动命令切换,时间为tsw=2.5 s,大小为at,max=5g,三方的实际飞行速度分别取为vt=290 m/s,vd=505 m/s,vm=520 m/s,即假设存在一定的飞行速度误差,ad,max=10g,仿真结果如图8～图10所示。其中,图8为三方的飞行弹道,最终的脱靶量为0.076 m,满足了LOS制导的要求。图9和图10分别为防御导弹的加速度变化曲线和误差角曲线。从图中可以看出,制导律CASD不仅可以实现对攻击导弹的有效拦截,且对其机动和三方的飞行速度误差具有较强的鲁棒性。

图8 飞行弹道

图9 防御导弹的加速度

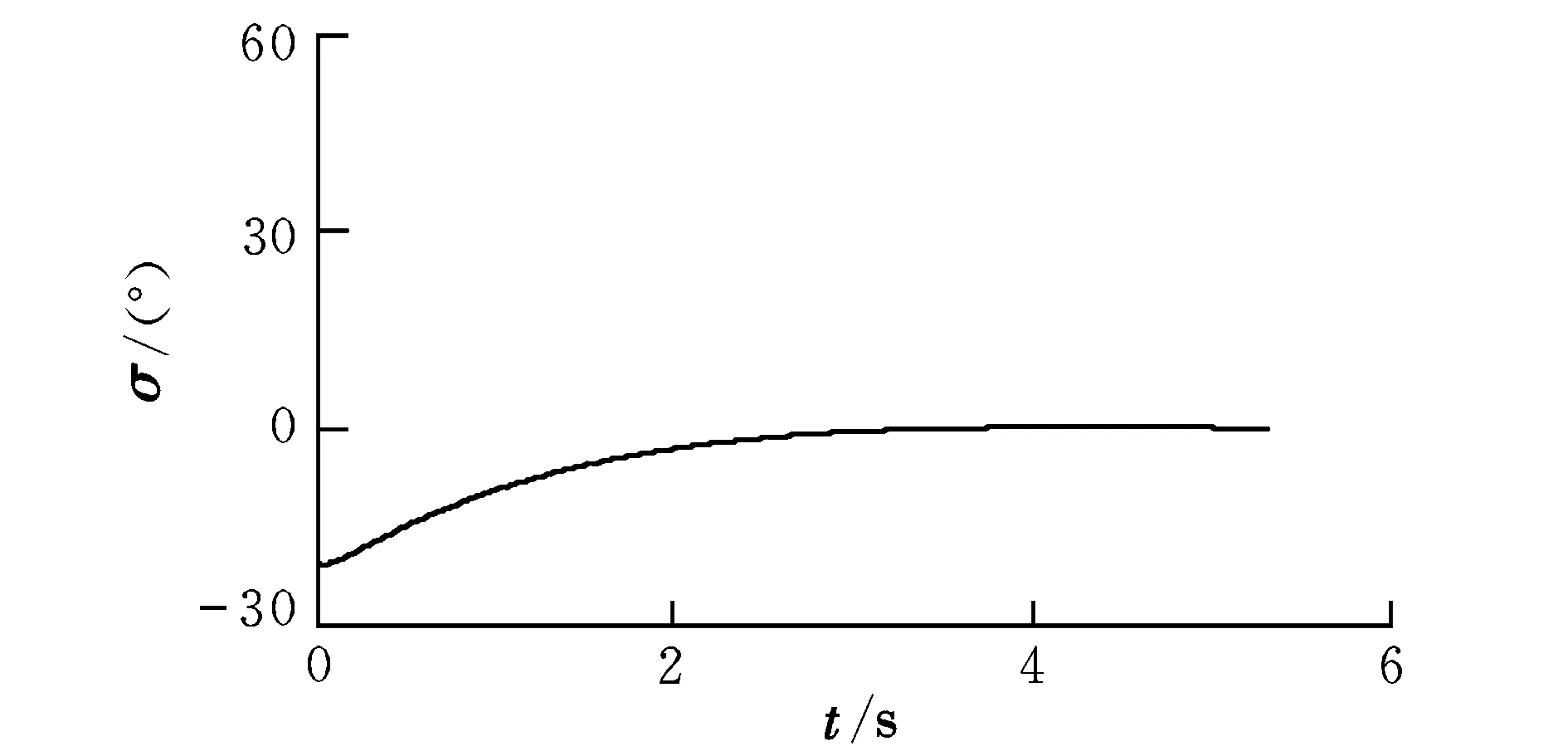
图10 误差角

4 结束语

基于滑模控制方法,设计了一种飞机与防御导弹协同对抗攻击导弹的自适应制导律,该制导律有效地满足了LOS的制导要求,相比于PN制导律具有明显的性能优势,且对三方飞行速度误差和防御导弹机动具有较强的鲁棒性。该制导律很容易扩展到三方具有高阶机动动态和存在其它系统不确定性的情形。

[1] Asher R,Matuszewski J.Optimal guidance with maneuvering targets [J].Journal of Spacecraft,1974,11(3):204-206.

[2] Boyell L R.Defending a moving target against missile or torpedo attack [J].Transactions on Aerospace and Electronic Systems,1976,AES-12(4):522-526.

[3] Rusnak I.Acceleration requirements in defense against missile attack [C]//The 47th Israel Annual Conference on Aerospace Science.Tel Aviv,Israel,2007:1-6.

[4] Rusnak I.Guidance laws in defense against missile attack [C]//IEEE 25th Convention of Electrical and Electronic Engineers in Israel. Eilat,Israel,2008:90-94.

[5] Shaferman V,Shima T.Cooperative multiple model adaptive guidance for an aircraft defending missile [C]//AIAA Guidance,Navigation,and Control Conference.Toronto,Canada:AIAA Press,2010:1-25.

[6] Shinar J,Turetsky V,Oshman Y.Integrated estimation/guidance design approach for improved homing against randomly maneuvering targets [J].Journal of Guidance,Control,and Dynamics,2007,30(1):154-161.

[7] Shinar J,Shima T.Nonorthodox guidance law development approach for intercepting maneuvering targets [J].Journal of Guidance,Control,and Dynamics,2002,25(4):658-666.

[8] Ratnoo A,Shima T.Line of sight guidance for defending an aircraft [C]//AIAA Guidance,Navigation,and Control Conference.Toronto,Canada: AIAA Press,2010:1-22.

[9] Lee G T,Lee J G.Improved command to line-of-sight for homing guidance [J].Transactions on Aerospace and Electronic Systems,1995,31(1):506-510.

[10] Benshabat D G,Bar-Gill A.Robust command to line-of-sight guidance via variable-structure control [J].Transactions on Control Systems Technology,1995,3(3):356-361.

[11] Shima T,Golan O M.Linear quadratic differential games guidance law for dual controlled missiles [J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):834-841.

[12] Shinar J,Steinberg D.Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model [J].Journal of Aircraft,1977,14(8):795-802.

Cooperativeguidancelawforactiveprotectionbasedonadaptivesliding-modecontrol

HUA Wen-hua1,2, CHEN Xing-lin2, SONG Chao3

(1.Department of Control System, Luoyang Electro-Optics Development Center, Luoyang 471009, China;2.School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;3.The 10th Department, Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

As compared with the attacking missile, the aircraft has the disadvantages of flight velocity and maneuverability. To improve the survivability, the aircraft can launch a defending missile to intercept the attacker and correspondingly, a cooperative guidance law of defending missile is presented based on adaptive sliding-mode control. This guidance law is a kind of line of sight (LOS) guidance approach in essence, which guide the defending missile to locate inside the LOS between the aircraft and the attacking missile for active defense. Finally, simulations are carried out compared to proportional navigation. The results show that this guidance law has advantages of maneuvering performance and intercepting performance because of the cooperation with the aircraft and has strong robustness to the velocity variations of the three bodies and the maneuver of the attacking missile.

guidance law; adaptive sliding-mode control; cooperation; line of sight guidance

2011-04-11;

2011-08-24

黑龙江省科技攻关计划基金资助(GZ06A104)

花文华(1983-), 男, 安徽淮北人, 博士研究生, 研究方向为飞行器制导。

TJ765.3

A

1002-0853(2012)01-0066-05

(编辑：姚妙慧)