高超声速弹性飞行器后体/外喷管建模与分析

祝强军, 唐硕, 谭艺明

(西北工业大学 航天学院, 陕西 西安710072)

高超声速弹性飞行器后体/外喷管建模与分析

祝强军, 唐硕, 谭艺明

(西北工业大学 航天学院, 陕西 西安710072)

考虑到全尺寸吸气式高超声速飞行器的机体弹性弯曲振动极易被激发,提出了一种包含机体弹性弯曲影响的外喷管建模和分析方法。该方法首先用虚拟激波膨胀波法确定剪切层的位置,然后用影响系数法求解外喷管中的准一维流,并用活塞理论修正后体下表面的压力。用该方法对一个全尺寸吸气式高超声速飞行器的后体/外喷管进行了仿真分析,结果表明,仅考虑低频、小振幅的后体弹性弯曲运动对外喷管性能的影响并不显著。

高超声速; 弹性; 外喷管; 影响系数; 活塞理论

引言

对于全尺寸的吸气式高超声速飞行器,其低阶弹性弯曲模态频率通常很接近其刚体运动频率,激励刚体运动的控制输入极易激发机体的低阶弹性弯曲模态。吸气式高超声速飞行器的典型特点是乘波体机体和超燃冲压发动机一体化设计[1-2],用飞行器的后体下表面和膨胀过程中形成的自由射流边界构成喷管,并称其为单面喷管、自由膨胀喷管或者外喷管[3]。自由射流边界又称为剪切层,它是发动机尾气与自由流的静压达到平衡时的边界。如果飞行器机体发生弯曲振动,由于后体下表面的形状发生变化,剪切层也将发生变化,因此外喷管的膨胀性能将会改变,最终导致尾气对后体下表面作用力的大小和方向发生变化。因此,建模分析机体发生弹性振动对后体气动和推进特性产生怎样的变化,对于设计全尺寸的吸气式高超声速飞行器具有特别重要的指导意义。

D K Schmidt[4]最先建立了包含机体弹性变形影响的吸气式高超声速飞行器动力学解析模型。Schmidt将飞行器看作一个倒三角形,机体弹性变形用前体和后体绕倒三角顶点的转动来表示,后体压强用一个近似公式表示。用Schmidt的解析模型来分析吸气式高超声速飞行器后体气动和推进特性存在下列不足之处:首先,飞行器的真实振型与绕倒三角顶点的转动可能有较大差异,Schmidt没有明确给出使用这种简化振型的依据;第二,后体压强近似公式不能用于分析飞行器机体弹性变形引起剪切层变化和尾气沿后体非理性膨胀的情况。Bolender和Doman[5]扩展了Schmidt的飞行器模型,使其包含超燃冲压发动机通道,但是对飞行器后体的建模仍然采用Schmidt的近似公式。

针对前人工作存在的上述不足,本文以一个全尺寸吸气式高超声速飞行器为研究对象,建模分析了机体弹性弯曲振动对飞行器后体气动和推进性能的影响。机体弹性弯曲振动采用更真实的两端自由梁模型。提出了先用虚拟激波膨胀波理论确定剪切层位置,然后用影响系数法求解准一维流,并用活塞理论修正后体压强的分析方法。最后用一个具体的算例分析了后体弹性弯曲对外喷管性能的影响。

1 机体纵向弹性弯曲振动的描述

吸气式高超声速飞行器的细长形机体可以近似看作两端自由的弹性梁,其纵向弯曲方程为:

(1)

式中,w(x,t)为弯曲位移;EJ(x)为弯曲刚度;m(x)为单位长度的质量;p(x,t)为载荷集度。利用自由振动模态函数,式(1)的解可用分离变量法表示为:

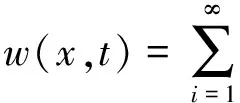
(2)

式中,φi(x)为第i阶自由振动模态函数;ηi(t)为第i阶模态的广义坐标。将式(2)代入到式(1)中,考虑结构阻尼的影响,增加结构阻尼项后可得:

(3)

式中,ξi为结构阻尼比,通过对实际结构做实验可以测出,其值通常小于0.1。忽略结构阻尼的影响,式(3)的通解为:

(4)

在飞行过程中,如果气动载荷与机体弹性运动发生耦合作用时,其弯曲振动可能会出现振幅不衰减的情况。考虑临界情况,即机体作简谐振动的情况下对吸气式高超声速飞行器压缩系统产生什么影响,此时广义坐标表示为:

ηi(t)=ηi(0) cos(ωit)

(5)

2 后体/外喷管分析方法

吸气式高超声速飞行器后体下表面和位于其下方的剪切层构成了发动机的外喷管。高温、高压尾气将在外喷管中继续膨胀。因此,建模分析机体弹性振动对后体/外喷管的影响时,首先需要确定剪切层的位置,然后对外喷管中的流动进行分析。

2.1 虚拟激波膨胀波法——确定剪切层位置

图1 确定剪切层位置的虚拟激波膨胀波法

在外喷管自由射流边界两侧的流体具有相同的静压和速度方向,但是速度的大小并不相同。由于自由射流边界存在很大的速度梯度,通常将其称为剪切层。剪切层两侧流体的法向速度为零,因此剪切层可以看作是虚拟的不可穿透的固壁面。将外喷管沿流动方向划分为若干微段,当每一微段都足够短时,该微段的剪切层可用一平板代替。如图 1所示,对于某一外喷管微段,尾气将从主流方向通过膨胀波偏转羽流角θ转向虚拟平板方向;自由流将通过斜激波偏转同样大小的θ转向虚拟平板方向。这个θ可根据尾气的静压等于自由流静压来确定。具体来讲,先假定一个θ,然后求解尾气流偏转θ的Prandtl-Meyer膨胀波方程,求解自由流偏转θ的斜激波方程,如果尾气流和自由流的静压不同,则重新选择θ,重复上述过程直到获得某个θ使得尾气流和自由流的静压相等。如果尾气流与自由流的压强比高于某个极限值,那么使尾气流与自由流压强相等的偏转角就可能接近90°或者不存在。如果θ接近90°,则外喷管的面积变化为无穷大,为了保证准一维流假设的合理性,压强比高于极限值时可以设置θ为75°[6]。

2.2 影响系数法——求解外喷管中的准一维流

驱动准一维流参数变化的因素有:截面积变化、壁面摩擦、热传递、机械功、质量注入、体积力、化学反应等。仅单个因素作用的简单流通常可以获得解析解,而多个因素同时作用的复杂流通常需要数值求解流体控制微分方程组。外喷管中的流动可看作具有面积变化和壁面摩擦的复杂流。将外喷管沿流动方向划分为若干足够短的微元段,然后利用微分形式的流体控制方程组对微元逐段求解就可得到外喷管流场的解。对图 2所示的微元控制体,Shapiro[7]推导了流体控制方程的微分形式,并以式(6)～式(8)中的影响系数的形式给出。

图2 外喷管的微元控制体

(6)

(7)

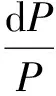
(8)

式中,γ为尾气流的比热容比;dA为微元面积变化;Cf为壁面摩擦系数,按文献[6]建议设为0.005;D为外喷管的水力半径；P和T分别为压强和温度。

dA=dx(tanθ+tanθn)

(9)

式中,θn为后体倾斜角。

D=4Ax/Px=4hx

(10)

式中,Ax为坐标为x处的外喷管横截面积;Px为该截面周长中存在壁面摩擦的那部分长度。

2.3 活塞理论——考虑弯曲速度对压强的影响

上述分析只考虑了机体弯曲位移引起外喷管截面积变化所产生的影响。由于机体在弯曲振动过程中,弯曲速度会对外喷管的尾气流产生扰动,因此需要对作用于后体下表面的压强进行修正。外喷管中尾气流的速度为超声速流,而低频弯曲振动的速度通常很小,在此前提下,可以假设后体下表面某一点的压强只与该点的下洗速度有关。假设外喷管中的准一维流是沿发动机轴线方向的,后体弯曲速度与该方向垂直,于是后体下表面尾气流的下洗速度为:

(11)

考虑到后体弯曲速度产生的下洗影响,可用活塞理论对后体压强进行修正。活塞理论认为,后体下表面某点的压强与该点的下洗速度有关,可用活塞在一维管道中运动时,其所受到的压强与其运动速度的关系来比拟。活塞理论给出压强公式为:

(12)

式中,P∞和a∞分别为未受弯曲速度扰动的尾气流的压强和声速。

3 算例与分析

3.1 基本参数

以一个总长为30.5 m的全尺寸吸气式高超声速飞行器为例,假定其在高度30 km、Ma=7 巡航飞行时,机体受到某种扰动作用而发生弹性弯曲谐振,并假设机体振动引起的发动机入口条件的变化可以通过发动机的控制来补偿,因此可以认为外喷管入口处的尾气流动参数保持不变(具体见表1)。在此前提下,计算和分析后体的气动和推进特性。

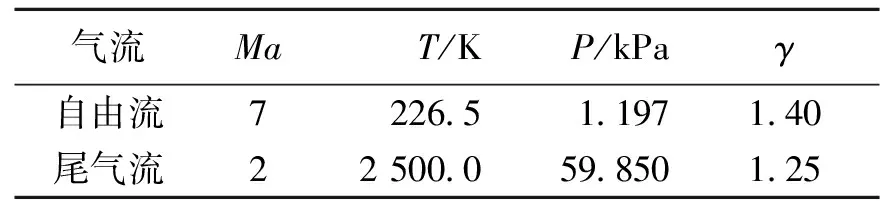
表1 外喷管的入口条件

3.2 振动位移的影响

后体发生弹性振动将引起剪切层位置的变化,进而引起外喷管横截面积的变化。一般来说,剪切层的位置主要取决于其起始位置,沿着x方向跟随后体振动而上下移动,但是移动量要小于后体的移动量(见图 3)。因此当后体上移时外喷管的横截面积增大,从而使马赫数增大,温度和压强减小;反之,后体下移时横截面积减小,从而使马赫数减小,温度和压强增大(见图 4)。

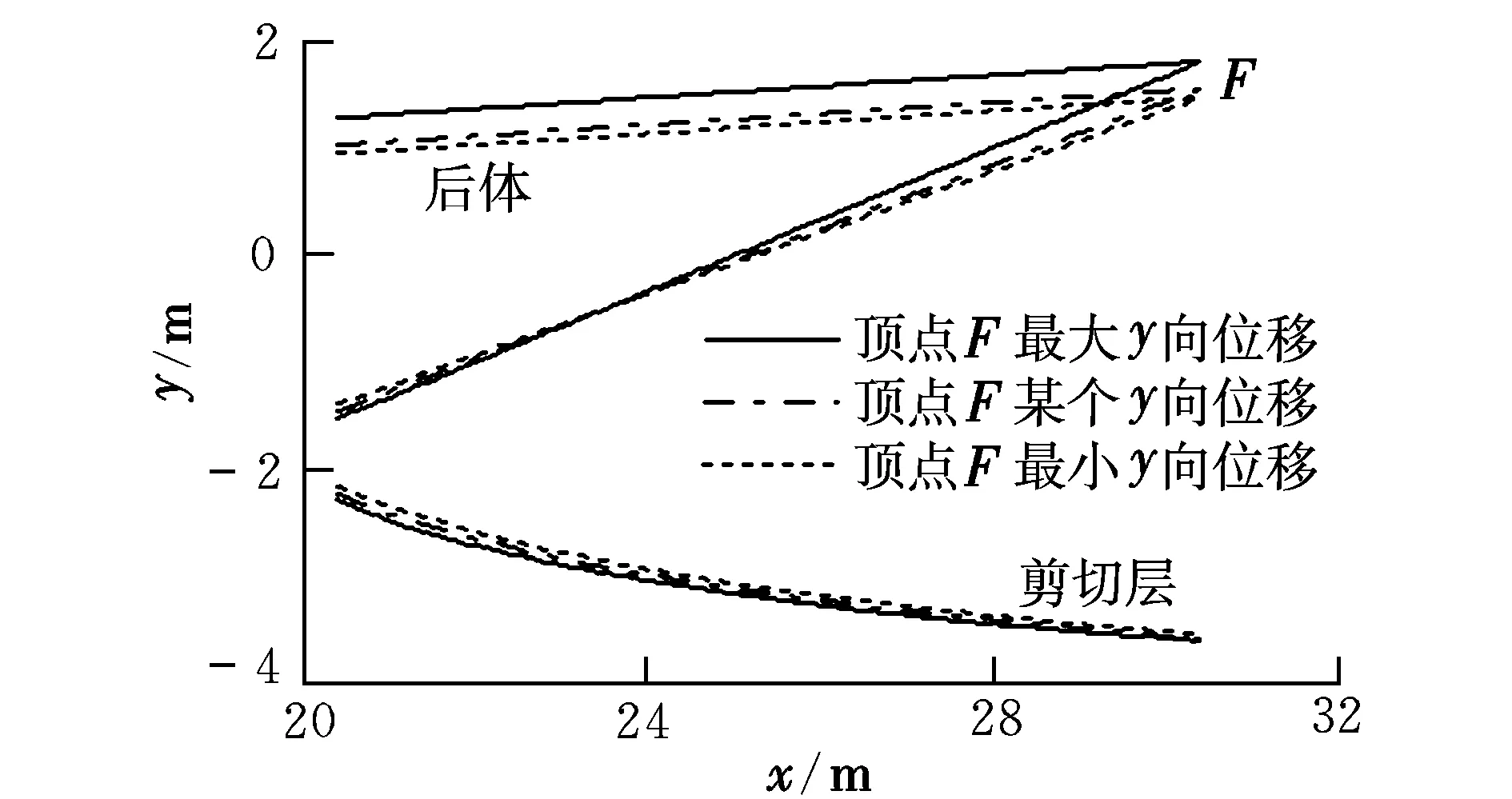
图3 后体/外喷管位置变化

图4 外喷管参数变化

图 4还给出了分别用Schmidt预测方法[4-5]和本文方法得到的飞行器后体下表面的压强分布曲线。由图可见,Schmidt预测的压强要明显低于本文计算得到的压强值。这是因为Schmidt的后体压强分布公式是根据外喷管理想膨胀得到的,而高超声速推进系统的外喷管通常工作在欠膨胀状态。另外,弹性变形引起的压强分布变化量远小于Schmidt预测的误差量,从这个意义上看,用Schmidt预测法来考虑弹性变形影响是值得商榷的。

3.3 摩擦和振动速度的影响

图 5所示的是机体振动频率为25 Hz、振幅为0.6%总长时,分别考虑弹性振动位移影响、弹性振动位移加上摩擦作用影响、弹性振动位移和速度加上摩擦作用影响三种情况下,后体压力和压心的变化情况。

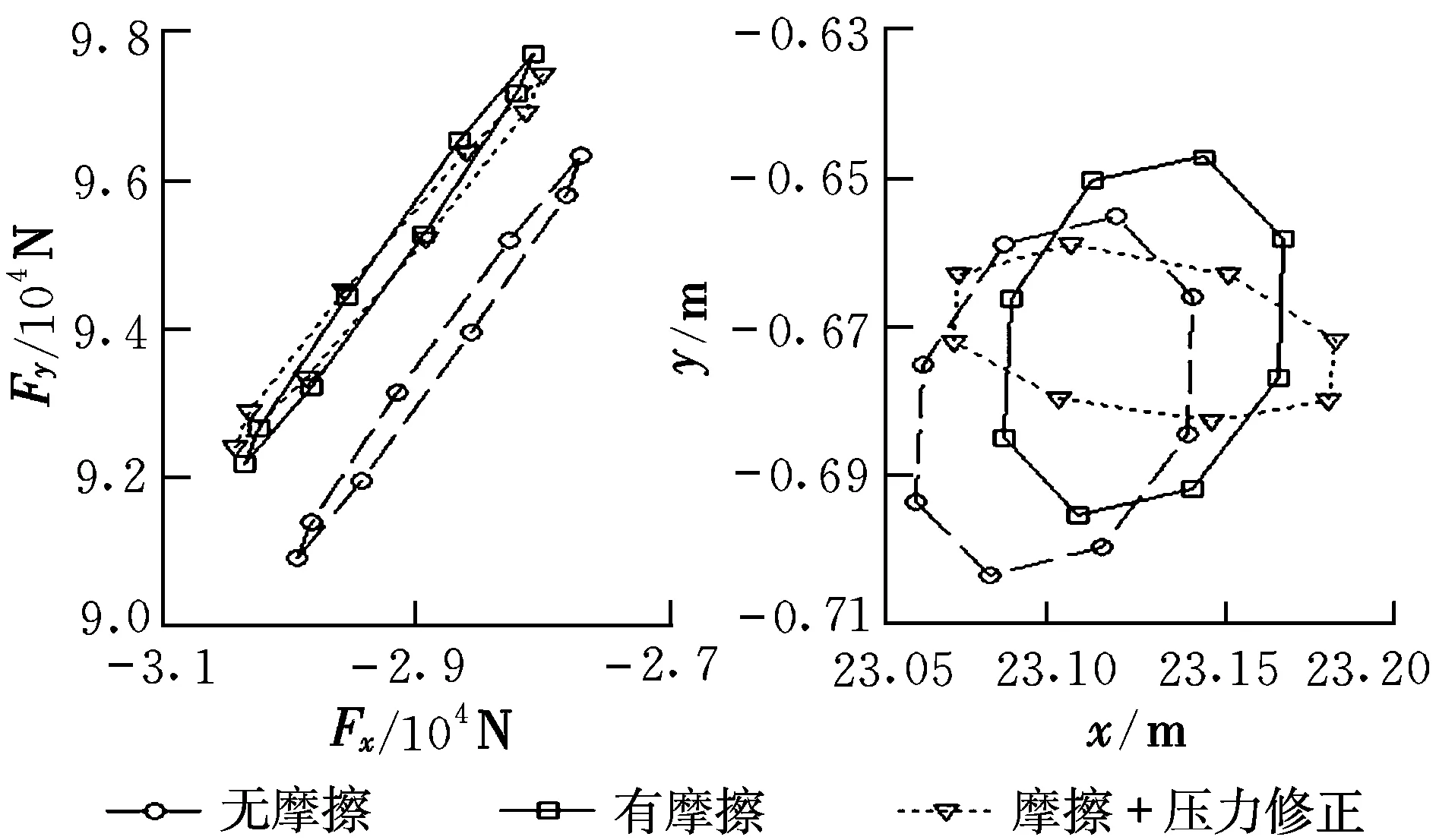
图5 后体压力矢端轨迹和压心轨迹

由图5可知,在尾气流向外喷射过程中,由于后体下表面的摩擦作用,尾气作用于后体的压强在有摩擦情况比无摩擦情况下沿x方向下降要缓慢些。与无摩擦情况相比,有摩擦情况下尾气作用于后体压力要大一些,压心位置靠后一些。如果再考虑到弯曲速度的影响,利用活塞理论对后体下表面的压力进行修正,后体压力变化量并不大,但是压力的相位会产生一个超前量,压心在y方向的变化范围变小。

图6所示的是考虑后体摩擦作用和忽略后体摩擦作用情况下的总压比变化情况。由图6可知,振动引起的总压比变化相对较小,而摩擦作用引起的总压比下降十分明显。

图6 总压比变化

3.4 机体振动频率的影响

图 7所示的是机体振幅为0.6%总长时,振动频率分别为5 Hz,25 Hz和50 Hz情况下的后体下表面压力和压心在振动过程中的变化曲线。

图7 不同频率的后体压力矢端轨迹和压心轨迹

从图 7可以看到,随着振动频率的增大,弯曲速度的影响不断增强,y方向压力变化范围趋于缩小,但是压心位置变化范围更大了。

3.5 机体振动幅值的影响

图8所示的是机体振动频率为25 Hz时,振幅分别为0.4%,0.6%和0.8%总长的情况下的后体下表面压力和压心在振动过程中的变化曲线。由图 8可以看到,后体下表面压力与压心位置变化范围几乎与振幅成正比增大。

图8 不同振幅的后体压力矢端轨迹和压心轨迹

4 结论

通过对吸气式高超声速弹性飞行器的后体/外喷管的建模和分析,可得到下列结论:

(1)对于全尺寸的吸气式高超声速飞行器,其低阶的机体弹性弯曲振动极易被激发。对于所关心的低频、小振幅机体弹性弯曲振动而言,如果单独考虑后体/外喷管在振动过程中的影响,可以发现其影响并不是特别显著;

(2)文中的算例是在一阶固有振动情况下计算得到的,在二阶固有振动情况下变化趋势将有所不同,但只要是在小振幅条件下,后体弹性运动的影响同样不是那么显著;

(3)文中通过假设后体/外喷管入口参数在机体振动过程中保持不变,考察了后体弹性弯曲振动产生的影响。由于吸气式高超声速飞行器机体/发动机一体化设计的特点,如果考虑到前体弯曲产生的扰动传递到后体所产生的影响,则还需要进一步分析。

[1] Javaid K H,Serghides V C.Airframe-propulsion integration methodology for waverider-derived hypersonic cruise aircraft design concepts[C]//The 42nd AIAA Aerospace Sciences Meeting and Exhibit. USA:Reno,Nevada,2004:1-10.

[2] Lewis M J.A hypersonic propulsion airframe integration overview[C]//The 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.USA:Huntsville,Alabama,2003:1-11.

[3] Schmidt D K,Mamich H,Chavez F R.Dynamics and control of hypersonic vehicles the integration challenge for the 1990’s[C]//The 3rd AIAA International Aerospace Planes Conference.USA:Orlando,FL,1991:1-10.

[4] Chavez F R,Schmidt D K.Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis[J].Journal of Guidance,Control,and Dynamics,1994,17 (6):1308-1319.

[5] Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44 (2):374-387.

[6] Brewer K M.Exergy methods for the mission-level analysis and optimization of generic hypersonic vehicles[D].Blacksburg,Virginia:Virginia Polytechnic Institute and State University,2006.

[7] Shapiro A H.The dynamics and thermodynamics of compressible fluid flow[M].New York: John Wiley and Sons,1953.

Modelingandanalyzingtheafterbodyexternalnozzleofaflexiblehypersonicflightvehicle

ZHU Qiang-jun, TANG Shuo, TAN Yi-ming

(Collage of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

To investigate the influence of airframe bending vibration on external nozzle for full-scale airbreathing hypersonic flight vehicles (AHFV), a new method is developed for modeling and analyzing the external nozzle of AHFVs under the airframe vibration. The first step of this method is to determine the shear layer position using virtual shock-expansion wave method. After that, the flow in the external nozzle modeled as quasi-one dimensional flow is solved using the influence coefficients method, and the pressure on the lower surface of afterbody is modified by the piston theory. To analyze the influence of airframe bending vibration on external nozzle performance, a simulation is carried out using the new developed method. The results show that the change of an external nozzle performance is not so remarkable, as long as the airframe bending motion is in the range of low frequency and small amplitude.

hypersonic speed; flexibility; external nozzle; influence coefficien; piston theory

2011-03-11;

2011-07-27

祝强军(1982-)，男，浙江江山人，博士研究生，研究方向为高超声速飞行器动力学与控制。

V411

A

1002-0853(2012)01-0048-05

(编辑：姚妙慧)