倾斜转弯高超声速飞行器滑模变结构解耦控制

熊柯, 夏智勋, 郭振云

(国防科学技术大学 航天与材料工程学院, 湖南 长沙 410073)

倾斜转弯高超声速飞行器滑模变结构解耦控制

熊柯, 夏智勋, 郭振云

(国防科学技术大学 航天与材料工程学院, 湖南 长沙 410073)

针对在倾斜转弯时高超声速飞行器自动驾驶仪设计中系统参数不确定和干扰严重、各通道之间存在强烈耦合的问题,提出了一种全局积分滑模变结构解耦控制方法。该方法基于滑动模态对匹配的参数不确定和外界干扰的不变性原理,采用了一种全局积分型的滑模面,使系统在初始阶段就处于滑模态,同时通过滑模函数反馈削弱参数摄动及干扰产生的滑模误差,实现了各输出之间的全程解耦和鲁棒稳定。仿真结果证实了所提方法具有良好的跟踪性能和鲁棒性,能满足高超声速飞行器倾斜转弯协调控制的要求。

倾斜转弯; 高超声速; 解耦设计; 全局积分滑模

引言

倾斜转弯技术可以满足高超声速飞行器气动外形与冲压发动机兼容的要求,保证超燃冲压发动机处于良好的工作状态,提高迎角使用范围,增强飞行器的侧向机动能力和滚动稳定性。但由于飞行器外形不对称,同时要绕速度矢量快速滚转,导致了飞行器动力学中必然存在三种耦合:气动耦合、运动学耦合和惯性耦合[1-3],通道间的耦合使得飞行器在倾斜转弯时容易诱发较大的侧向过载和侧滑角,而倾斜转弯协调控制要求侧滑角近似为零,这使得高超声速飞行器自动驾驶仪的解耦设计成为关键问题。

由于飞行器在高超声速飞行中气动系数不确定性严重,而且还会受到各种干扰,因此要保证控制系统快速、精确的控制,就需要保证三通道解耦的同时具有强鲁棒性。滑模变结构控制是一种很好的鲁棒解耦设计工具,其鲁棒解耦的理论基础是滑动模态的不变性原理,具有滑动模态的变结构系统对外界干扰和参数摄动有很强的鲁棒性[4-6]。为了在输出解耦的基础上消除系统的稳态误差、削弱系统参数不确定和干扰对系统的动态影响,本文设计了一种全局积分滑模控制器,使系统在初始阶段就处于滑模态,同时通过滑模函数反馈减小了系统参数不确定和干扰造成的滑模误差,实现了各输出之间的全程解耦和鲁棒稳定。

1 飞行器动力学模型

令系统状态x=[α,β,γ,ωx,ωy,ωz,φ,ψ]T,控制量u=[δz,δy,δx]T,系统输出y=[α,β,γ]T,则倾斜转弯高超声速飞行器非线性控制模型描述如下:

(1)

式中,f(x),B(x)和h(x)分别为x的n维、n×m维和m维解析向量函数;Δf(x)为系统函数中的不确定项;ΔB(x)为系统输入矩阵中的不确定项;d(x)为未建模动态和外部干扰。

f(x)=

(2)

(3)

h(x)=[h1(x),h2(x),h3(x)]T

=[α,β,γ]T

(4)

2 三通道全局积分滑模解耦控制

采用如下形式的传统滑模面:

s=[s1,s2,s3]T

(5)

式中,λi>0 (i=1,2,3)。λi使得以下系统

(6)

是渐近稳定的。

采用一定形式的滑模趋近律得到控制作用,当系统在控制作用下到达滑动模态时,有:

(7)

各个误差方程都只与自身动态相关,因此系统的各输出之间没有耦合作用。在实现滑模运动的同时,系统也实现了解耦输出。

传统的滑模控制形式简单、易于设计实现,但是由于初始误差、系统不确定和干扰会引起滑模误差,而系统没处于滑模态时各输出之间存在耦合,会影响滚动角和迎角的动态响应,同时使得侧滑角动态增大,而较大的侧滑角会引发大的诱导滚动力矩,进一步加强交叉耦合效应,严重影响倾斜转弯飞行器的控制性能。

由式(7)易知,系统的各输出之间保持解耦状态的关键是在系统存在不确定和干扰的情况下保持滑模态,本文提出的解决办法是设计全局积分型的滑模面,增强系统的鲁棒性,同时使得系统一开始就处于滑模面上,消除了到达阶段,实现各输出之间的全程解耦。

设计如下形式的滑模面:

σ=[σ1,σ2,σ3]T

(8)

式中,en为自然对数;mi>0;ηi>0;ei(0)(i=1,2,3)为初始误差。

由于σ(0)=[0 0 0]T,系统从一开始就处于滑模态,假设不确定系统式(1)满足广义匹配条件[7],于是有:

(9)

其中:

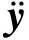
q(x)=[LdLfh1(x),LdLfh2(x),LdLfh3(x)]T

式中,L为Lie导数算子;p(x),Δp(x),G(x),ΔG(x)的具体表达式见文献[7]。

由于G(x)是非奇异的,所以可取:

(10)

其中:

K=diag[k1,k2,k3],L=diag[l1,l2,l3]

(ki>0,li>0;i=1,2,3)

sgnσ=[sgnσ1,sgnσ2,sgnσ3]T

将式(10)代入式(9)可得到滑动模态趋近律:

(11)

Δp(x)+ΔG(x)u+q(x)=δ(x)

于是式(11)为:

(12)

式(12)表明广义不确定性δ(x)的存在会引起滑模误差,进而严重影响各输出的动态响应,因为δ(x)是时变不确定的,难以准确估计和消除,所以通过滑模函数反馈的形式削弱其影响,取控制律:

Kσ-Lsgnσ)

(13)

其中:

于是有:

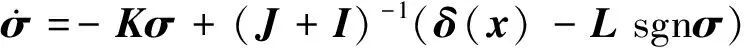
(14)

图1为滑模函数反馈示意图。

图1 滑模函数反馈示意图

=σT[-Kσ+(J+I)-1(δ(x)-Lsgnσ)]

≤-σT[Kσ-(J+I)-1Wsgnσ]

(15)

为了消除高频颤振现象,通常对变结构控制中的符号函数项sgnσ采用饱和函数来平滑,即取控制信号:

2.2 暴露方式及部位 暴露方式：锐器伤82名、占68.91%，黏膜暴露17名、占14.29%，皮肤暴露15名、占12.60%，其他5名、占4.20%；暴露部位：手指95名、占79.83%，手臂17名、占14.29%，眼7名、占5.88%。

Kσ-Lsat (σ/ρ))

(16)

其中:

sat(σ/ρ)=[sat(σ1/ρ1),sat(σ2/ρ2),sat(σ3/ρ3)]T

式中,sat(σi/ρi)为饱和函数;ρi为边界层厚度;i=1,2,3。定义:

在自动驾驶仪设计中,俯仰/偏航通道一般按照过载进行设计,因为迎角α、侧滑角β不易测量,但是考虑到高超声速飞行器的动力装置——超燃冲压发动机的推力大小与迎角、侧滑角直接相关,需要直接实施控制,因此在设计中将迎角和侧滑角作为状态变量和输出变量。在工程应用中,可利用惯导及其他测量信息估计出迎角、侧滑角。根据协调控制要求,可直接令侧滑角指令βr=0,迎角指令由文献[8]的方法产生。

3 仿真与分析

高超声速飞行器滑模变结构解耦控制系统仿真分析在Matlab/Simulink平台上展开。仿真参考信号为yr=[αr,βr,γr]T=[6°,0°,30°]T;舵机时间常数为0.01 s,阻尼系数为0.7;速率陀螺时间常数为0.003 2 s,阻尼系数为0.6。系统参数误差考虑极限情况,进行±30%拉偏,干扰作用根据力矩平衡关系等效为舵偏干扰d。

具体仿真参数为:

λ1=λ2=λ3=30 s-1,m1=m2=m3=15 s-1

η1=η2=η3=10,k1=15 s-1,k2=k3=10 s-1

l1=l2=l3=10 rad/s2,j1=j2=j3=5

w1=w2=w3=0.1 rad/s2,ρ1=ρ2=ρ3=0.2 rad/s

δz=δy=δx∈[-20°,20°]

仿真根据干扰分别为常值、时变和短时强干扰三种状态展开,即:

状态1:

d=[-5°,-5°,-5°]T

状态2:

d=[-5° sin(πt),-5° sin(πt),-5° sin(πt)]T

状态3:

d=[dz,dy,dx]T

式中,dz为周期1 s、幅值10°的方波;dy为周期2 s、幅值10°、延迟1 s的方波;dx为周期4 s、幅值10°、延迟2 s的方波。偏航和滚动方向的干扰引入延迟是为了考查干扰的耦合影响。仿真结果见图2～图4。

从图2～图4可知,在滑模控制器作用下,系统参数不确定对α,β,γ的响应影响不大,但是传统滑模控制器抑制干扰的能力差。状态1传统滑模控制器作用下,α,β,γ的稳态误差分别为0.15°,0.3°和3.2°,β和γ超调比较大,其中γ最大超调达到了12.3°,β最大超调达到了4°,而全局积分滑模控制没有产生超调和稳态误差;状态2传统滑模控制器作用下,γ振荡幅值达到了3°,β也有最大1.8°的误差,全局积分滑模控制只有γ产生了不大于0.2°的误差;状态3传统滑模控制器作用下,干扰在三个通道之间存在耦合,偏航和滚动通道尤其明显,α,β,γ的最大误差分别达到0.5°,0.75°和6.5°,全局积分滑模控制作用下,α,β,γ的最大误差分别为0.1°,0.05°和0.3°。仿真说明在干扰严重时,传统滑模控制器产生了较大的控制误差,不满足解耦控制要求,而全局积分滑模控制器对参数不确定和干扰都有很好的鲁棒性,保证了跟踪效果。

图2 状态1响应曲线

图3 状态2响应曲线

图4 状态3响应曲线

4 结束语

本文设计了一种基于全局积分滑模面的变结构解耦控制器,解决了传统滑模控制抑制干扰能力差、到达阶段存在耦合的问题,同时通过滑模函数反馈削弱参数摄动及干扰产生的滑模误差,实现了各输出之间的全程解耦和鲁棒稳定。仿真结果证实了本文所提方法具有良好的跟踪性能和鲁棒性,滚动角和迎角能精确控制,侧滑角保持在±0.5°以内,表明该自动驾驶仪能满足高超声速飞行器倾斜转弯协调控制的要求。

[1] Lee S Y,Lee J I,Ha I J.Nonlinear autopilot for high maneuverability of bank-to-turn missiles[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(4):1236-1253.

[2] Fu L C,Chang W D,Yang J H,et al.Adaptive robust bank-to-turn missile autopilot design using neural networks[J].Journal of Guidance,Control,and Dynamics,1997,20(2):346-354.

[3] Williams D E,Friedland B.Modern control theory for design of autopilots for bank-to-turn missiles[J].Journal of Guidance,Control,and Dynamics,1987,10(4):378-386.

[4] Chern T L,Wu Y C.Design of integral variable structure controller and application to electrohydraulic velocity servosystems[J].IEE Proceedings-D,1991,138(5):439-444.

[5] 张科,周凤歧.不确定性多变量系统的全程滑态变结构控制方案设计[J].控制理论与应用,1999,16(2):221-224.

[6] 李鹏,马建军,李文强,等.一类不确定非线性系统的改进积分型滑模控制[J].控制与决策,2009,24(10):1463-1466,1472.

[7] 李裕山,姚郁.再入飞行器的大机动轨迹实现[J].哈尔滨工业大学学报,1997,29(5):89-92.

[8] 张友安,杨旭,崔平远,等.BTT导弹的神经网络自适应反馈线性化控制[J].航空学报,2000,21(1):84-86.

Decouplingcontrollerdesignforbank-to-turnhypersonicvehiclebasedonslidingmodevariablestructure

XIONG Ke, XIA Zhi-xun, GUO Zhen-yun

(College of Aerospace and Material Engineering, NUDT, Changsha 410073, China)

An adaptive global integral sliding mode control approach is proposed to face the uncertainties and the serious cross coupling among the channels of hypersonic vehicle. This method is based on the invariant principle of sliding mode for uncertainties and disturbance, a global integral sliding is introduced, which makes the initial state of the system to locate at the sliding mode. The sliding mode error caused by disturbance and parameter perturbation is weakened with feedback, which decouples the output of the system and makes the system robust. Numerical simulation proves the efficiency and the robustness of the proposed algorithm, which satisfies the demand of the bank-to-turn hypersonic vehicle.

bank-to-turn; hypersonic; decoupling design; global integral sliding mode

2011-04-02;

2011-09-07

熊柯(1981-)，男，湖南桃江人，博士研究生，研究方向为飞行器鲁棒自适应控制。

TJ765.2

A

1002-0853(2012)01-0061-05

(编辑：姚妙慧)