从纽科姆难题看决策理论的两个原则

李 莉

(湖北大学 哲学学院， 湖北 武汉 430062)

从纽科姆难题看决策理论的两个原则

李 莉

(湖北大学 哲学学院， 湖北 武汉 430062)

纽科姆难题是一个与合理行动相关的决策困境问题。处于纽科姆难题决策情形中的决策者，根据决策理论中的两个基本原则——效用最大化原则和占优策略原则，得出了完全相反的两个结论，使得决策者无法确定什么才是合理的行动。对此难题，艾尔斯提出了修改最大化效用原则的方案，吉伯德和哈珀则提出了U效用和V效用的解决方案。

纽科姆难题；最大化效用原则；占优策略原则

一、纽科姆难题

物理学家威廉·纽科姆(W.Newcomb)在考虑囚徒困境问题的过程中，首先构造出纽科姆难题。罗伯特·诺齐克(R.Nozick)了解到这个难题后，于1969年撰写了一篇著名的论文《纽科姆难题和决策的两个原则》[1]，标志着纽科姆难题的正式提出。

纽科姆难题体现了作为决策论中最重要且最基本的两个原则，也就是最大化效用原则与占优原则之间的冲突。诺齐克在《理性的性质》一书中谈到纽科姆疑难研究之意义时写道：“经济学家和统计学家已经发展出一种有关合理决策的精心制作的理论，并将其广泛运用到理论与政策研究之中。这是一种具有数学严格性的，既强有力而又容易掌握的理论。虽然它作为实际行为的描述之充分性已受到广泛质疑，它仍然是有关合理决策所应满足条件之研究中居于支配地位的标准理论。我认为，这种标准决策理论需扩充到与行为的符号意义及其他有关因素的明晰思考相结合，而关于当前标准理论之不充分性认识的一个有益入口，是由纽科姆问题提供的。”[2]

在学界，纽科姆难题因此引起了广泛的关注。纽科姆难题有很多版本，以下采自诺齐克最原始的表述：

假定一个拥有超能力的生物，他能够预测你的选择(或者你也可以把它想象成一个科幻故事，一个外星来的生物，拥有先进的科学技术，同时也是非常友好的，等等)。你知道这个生物过去常常能正确地预测出你的选择(并且，至少到目前为止，对你的选择没有作过错误的预测)。此外，你知道这个生物经常正确地预测到其他人的选择，而且其中很多人都处于与你类似的情形中。当然，你可以发挥想象力，把故事讲得更长，但要点是：所有的描述都是让你相信这个生物对你的选择的预测都是正确的。

现在有两个盒子放在你面前：盒子B1，里面有1 000美元；盒子B2，里面现在是空的。你面临两个选择：或者只拿走B2，或者同时拿走两只盒子。然而对超级生物而言，(1)如果你只拿走B2，为了奖励你，他就放100万美元的奖金到盒子B2里面；(2)如果你贪心，拿走两只盒子，他就不往B2里面放钱。以上所有的决策信息你是知道的，并且超级生物也知道你是知道的，于是超级生物作出了预测，然后根据预测决定往B2里面放钱还是不放钱。同时你也知道这个超级生物知道你是知道的，而且盒子里面或者是空的或者有100万美元，现在请你决定：哪一个行动更为合理：拿走一只盒子，还是两只盒子？

在纽科姆难题的决策情形中，决策者必须在两个可能的行动中作出决定，有两种可能的世界状态，用t来表示时间，数字越大，表示时间越晚，数字相同，表示时间一样。据此，诺齐克给出了两个相反的但同样是合理的论证。两个不同的原则建议也不同，最大化条件效用的原则建议拿走一只盒子，也就是盒子B2，强占优原则建议拿走两只盒子。

(一)根据最大化条件效用原则得出“一盒论”的论证。

前提1：如果我在t3时拿走两只盒子，预言家将会在t1时以很高的概率预测到这些，并且在t2时不往B2里面放钱，所以我几乎能确定地拿到1 000美元。

前提2：如果我在t3时拿走B2，预言家会在t1时以很高的概率预测到这些，并在t2时放100万美元在B2里，所以我几乎能确定地拿到100万美元。

结论：因此我应当拿走B2。

论证过程：令C表示置信度，a1表示拿走两只盒子，a2表示拿走盒子B2，S1表示盒子里面有100万美元，S2表示盒子里面没有钱，表示假定决策者的置信度为：

c(s1|a1)=0.9

c(s1|a2)=0.1

c(s2|a2)=0.9

c(s2|a1)=0.1

并且假定决策者可能收益的效用是与可能的结果成线性增长，那么可能行动a1和a2的条件效用是这样计算的，其中CU表示期望效用，a1表示拿走两只盒子，a2表示拿走盒子B2：

CU(a1)=(0.9)(1 000)+(0.1)(1 001 000)=101 000

CU(a2)=(0.1)(0)+(0.9)(1 000 000)=900 000

因为CU(a2)比CU(a1)高，最大化条件效用原则推荐拿走盒子B2。

(二)根据占优原则给出“二盒论”的论证。

前提1：预言者已经在t1时作出了他的预言，把100万美元在t2时放入了B2中，或者没放。

前提2：假定预言者在t2时在B2中已经放入100万美元，如果我在t3时拿走两个盒子，我得到1 001 000美元，如果我在t3时拿走B2，我得到100万美元。

前提3：假定预言者t2时在B2中不放钱，如果我在t3时拿走两只盒子，那我得到1 000美元；如果我在t3时拿走两只盒子，那我得不到钱。

前提4：如果我拿走两只盒子而不是一只，那么在任何情况下，我都能多得1 000美元

结论：因此我应当拿走两只盒子。

假定对决策者而言，1 000美元的效用比0美元的效用高，1 001 000的效用比1 000 000的效用高，拿走两只的盒子行动明显优于拿走一只盒子，所以占优策略推荐拿走两只盒子。

这两个论证，在同一决策情形中，给出了完全相反的建议。诺齐克认为这体现了合理决策行动中两个决策原则之间的冲突，也就是期望效用最大化原则和占优原则之间的冲突。

二、期望效用最大化原则与占优原则

博弈论及一般决策理论的研究方法一般有两种：标准化研究方法和描述性研究方法。标准化方法，是探讨理想的理性主体的行为，目的是给出关于人们应当如何行动才是理性的描述。这种标准化研究方法的代表人物有杰弗里(Jeffery)、莱法(Raiffa)、斯基姆斯(skyrms)。标准化研究进路，是传统的研究途径。

这种进路上的决策理论认为有两个因素决定我们的决策。一是目标(或者愿望，或者需要)，二是信念。目标可以用客观效用或者主观价值来表征，信念则用置信度或者机会来表征。令效用的符号用U(客观效用是OU)，置信度用C，机会用Ch表示。决策效用用u(oij)表示。决策的效用排序如下：u1最低，u2较高，unm最高。

在杰弗里看来，对决策者效用的一个合理限制是满足愿望公理：对任意命题X,Y，如果c(X∩Y)=0，而且c(X∪Y)≠0，那么

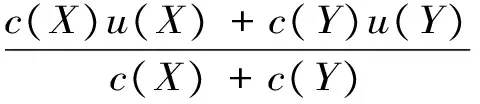
对置信度的限制是要求置信度满足数学概率计算的公理，也就是克洛莫诺夫公理*也就是：(1)非否定公理：事件A的概率高于或者等于0；(2)标准化公理：事件A和事件非A的合取概率为1；(3)限定添加公理：如果两个事件A和B的析取不为空，那么P(AB)=P(A)+P(B))。。这是一个融贯性要求，一旦违反就会使决策者产生不融贯的置信度，处于大弃赌情境中。

根据置信度，可以把决策分为三类：(1)如果决策者给可能行动赋予0或者1的置信概率，那么决策者面对的是确定性决策；(2)如果决策者赋予可能行动0

确定性决策中，行动方案是有限的，每个行动方案都有一个确定的结果，决策者需要做的是对各个行动方案的结果进行比较，因此，“确定性决策的合理性原则是效用最大化原则，即选择那个能使决策者获得最大效用的行动方案”[3]223。

风险型决策和不确定型决策的共同点是，备选的行动方案中，至少有一个方案的可能结果不止一个，从而使得哪一个方案具有最大效用也是不确定的。在这种情况下，就需要使用占优策略原则。

在风险型决策中，决策者虽然不知道哪种结果一定出现，但是可以知道每种结果出现的概率。而在不确定型决策问题中，没有客观概率可以依据，因此“这是一个困难大、争议多的问题，也是主观贝叶斯派着重研究的问题”[3]224。

下面是决策理论中常用的两个原则：

(一)效用最大化原则。

根据萨维奇的观点，决策者的行动效用可以用下面的公式来计算(用U(ai)来指称可能行动的效用)：

萨维奇宣称决策者应当依据效用最大化原则：在一个给定的决策情形D中，决策者X应当根据效用最大化来决定是否采取行动ai。

杰弗里要求决策者应当采取最大化条件效用的原则：在给定的决策情形D中，决策者X应当根据最大化条件效用的原则采取行动ai。

(二)占优原则。

决策论中经常使用的另一个相关原则是占优原则。准确地说，它其实是两个原则：强占优原则和弱占优原则，不过通常决策理论家不太在意二者之间的差异。

1、强占优：一个可能的行动ai在所有行动{a1,a2，…，an}{ai}中强占优，当且仅当对于每一可能世界s1,s2，…，sm状态，可能行动ai的收益效用与其他行动{a1,a2，…，an}{ai}的收益效用O11,O12，…，Onm相比，是较高的(表示不包含)。

2、强占优原则：在一个给定的决策情形D中，如果有最强的可能行动ai，决策者X应当决定采用最强的可能行动ai。

3、弱占优：一个可能的行动ai在所有行动{a1,a2，…，an}{ai}中弱占优，当且仅当对于可供考虑的可能世界s1,s2，…，sm，可能行动ai的收益效用至少在一种情况下与其他行动{a1,a2，…，an}{ai}的收益效用O11,O12，…，Onm相比，是较高的(表示不包含)，并且相对于可供考虑的可能世界S1,S2，…，Sm而言，能够带来与可能行动{a1,a2，…，an}{ai}的收益效用O11,O12，…，Onm相等的效用。

4、弱占优原则：在给定决策情形D中，如果有可能的弱占优行动ai，X则应当采用ai。

三、如何解决纽科姆难题

艾尔斯认为：“纽科姆难题能够并且也应当使用修改最大化条件效用的原则来解决。”[5]

在他看来，纽科姆难题有下面的因果结构：一个共同原因CC(cc1：p1和a1的共同原因，cc2：p2和a2的共同原因)；一方面带来一个预言P(P1：预言拿走两只盒子，P2:预言拿走盒子B2)，可能的收益±O(S1:B2里没钱，S2:B2里有100万美元)；另一方面引起某种元素R，可能的行动是±A(a1:拿走两只盒子，a2:拿走B2)。因此，艾尔斯认为纽科姆难题的因果结构在从共同原因±CC到可能收益±O之间增加了一个成员±P。

艾尔斯认为，如果决策者相信在预言和可能行动之间有很强的联系，决策者就应该相信预言者的成功背后有一个因果的解释；如果预言并没有带来可能行动，他认为预言成功背后唯一的解释就是预言和可能行动之间具有共同原因。

给定关于纽科姆难题的情境分析，艾尔斯试图显示决策者的信念会带来选择两个盒子的解决方案。通过对条件效用的计算就可以得出拿走2只盒子的解决方案。

刘易斯批评说：“艾尔斯的理论只能应用于理想的合理决策者。”[6]他认为，如果理性包含艾尔斯所宣称的自我知识，就有决策者在作出决策之前就知道他们会怎么做了。此外，还有自我意识的决策者，他们的决定会带来比思想实验更多的自我知识。刘易斯问道：为什么我们不问对部分理性决策者而言，什么决策是理性的，他们的部分理性决策方法是否会帮助他们找出理性的可能行动？此外，在纽科姆难题中，艾尔斯的理论对部分理性决策者而言，并没有给出正确的答案。

普莱斯(H.Price)则指出，艾尔斯的辩护是自指的。“艾尔斯的理想理性决策者不仅要知道他的相关信念是什么，目标是什么，也要知道这些信念和目标是否能引导他选择两个盒子。”[7]普莱斯继续指出，在艾尔斯的辩护中，还要回应更为严重的问题。对普莱斯而言，在纽科姆难题中，假定一个和决定拿走两只盒子相关的普遍原因比假定一个和事实上拿走两只盒子的相关的普遍原因更为自然。

吉伯德和哈珀指出，有两种预期效用、两种独立性和两种占优原则。一种预期效用是根据反事实(countfactuals)概率(吉伯德和哈珀所理解的“反事实”并不要求它的前提一定是假的)而计算出来的预期效用，他们称之为U效用；另一种预期效用是根据条件概率计算出来的预期效用，称之为V效用。两种独立性是因果独立性和随机独立性，两种占优原则是有因果独立性的占优原则和有随机独立性的占优原则。

吉伯德和哈珀说：“如果合理性要求U最大化,则有因果独立的占优原则适合，如果合理性要求V最大化,则有随机独立的占优原则适合。”[8]根据他们的分析和计算结果，“一盒选择”的V效用大于“两盒选择”的V效用,而“两盒选择”的U效用大于“一盒选择”的U效用。这与诺齐克的观点是完全不同的。诺齐克认为，纽科姆难题体现了预期效用最大化原则和占优原则之间的冲突，而在吉伯德和哈珀看来，问题在于两种预期效用最大化之间的冲突。

U效用是如何测量的呢？吉伯德和哈珀认为，理性的决策是用反事实条件概率来表示的。根据ai▯→Oj，意思是“如果我要做ai，那么就会得到Oj”。在决策的时候，一般说来，决策者如果实施某种可能行动时，他也不能确定地知道会得到什么结果，因而会给这样的虚拟条件赋予置信度。此时，决策者用效用计算他的可能收益，于是，一个可能行动的U效用可以用下面的方式来计算：

根据吉伯德和哈珀的观点，决策者应当使用最大化U效用的原则：在给定的决策情形D中，决策者X应当决定是否用最大化U效用来采取可能行动ai。

在纽科姆难题上，吉伯德和哈珀是这样论证的：最大化V效用建议只拿走盒子B2，因为它与杰弗里的最大化条件效用类似，最大化U效用的原则推荐拿走两只盒子，其论证如下：

假定S1的置信度是μ,S2的置信度是1-μ，因为s1和s2都是因果地独立于决策者的可能行动a1和a2，那么决策者的置信度为：

c(a1▯→s1)=μ

c(a2▯→s1)=μ

c(a1▯→s2)=1-μ

c(a2▯→s2)=1-μ

因此可能行动U效用的计算导出：

U(a1)=c(a1▯→s1)μ(1 000)+c(a1▯→s2)μ(1 001 000)

=1 000μ+(1-μ)1 001 000

=1 001 000-1 000 000μ

U(a2)=c(a2▯→s1)μ(0)+c(a2▯→s2)μ(1 000 000)

=μ(0)+(1-μ)1 000 000

=1 000 000-1 000 000μ

因为对每一U而言，U(a1)>U(a2)，最大化U效用的原则建议是拿走两只盒子。

对于吉伯德和哈珀的反事实条件理论，其问题在于假如反事实条件的前件是假的，也就是说，决策者可能相信形如ai▯→Oj的反事实条件可能实施，也可能不实施，这种情况下该怎么办？吉伯德和哈珀的回答是诉诸直觉，这显然不是一个令人满意的答案。

[1] R Nozick.Newcomb’s Problem and Two Principles of Choice in N Rescher[M]//D Davidson，C G Hempel.Essays in Honor of Carl G Hempel.Reidel，Dordrecht，1969:14-146.

[2] 张建军.逻辑悖论研究引论[M].南京：南京大学出版社，2002：222.

[3] 熊立文.现代归纳逻辑的发展[M].北京：人民出版社，2004：223.

[4] R C Jeffrey.The Logic of Decision[M].Chicago，London:The University of Chicago Press，1983:4.

[5] E Eells.Rational Decision and Causality[M].Cambridge:Cambridge University Press，1982:206.

[6] D Lewis.Causal Decision Theory[J].Australasian Journal of Philosophy 59，1981:10.

[7] H Price.Against Causal Decision Theory[J].Synthese 67，1986:204.

[8] A Gibbard，W L Harper.Counterfactuals and Two Kinds of Expected Utility[M]//C A Hooker，J J Leach，E F McClennen.Foundations and Applications of Decision Theory:vol.1.Reidel，Dordrecht，1978:125-162.

B815

A

1007-8444(2012)05-0613-05

2012-07-07

李莉(1974-)，博士，讲师，主要从事逻辑哲学、逻辑应用研究。

责任编辑：王荣江