基于合成车流的桥梁车辆荷载效应极值预测
2012-07-31周小燚
阮 欣,周小燚,郭 济
(同济大学 桥梁工程系,上海200092)
车辆荷载是影响公路桥梁安全和使用寿命的关键因素之一,建立特定地点(site-specific)的车辆荷载模型对新建桥梁设计和既有桥梁评估都具有十分重要的意义[1].现有规范的车辆荷载取值多基于部分区域的短期交通流采集,通过统计分析将数据结果扩展为统一的车辆荷载标准.这样的荷载标准适用于常规设计,对于精度要求更高的桥梁关键构件设计或是在役桥梁评估,应结合实际车辆荷载特征,研究建立特定地点车辆荷载模型.研究表明:小跨径桥梁的荷载效应受单个重车影响明显,其荷载模型主要关注车重、轴重、轴距等车辆数据;大跨径桥梁的车辆荷载需要考虑多辆车同时作用的情况,除基本的车辆数据外,还需进一步考虑车速、车头时(间)距、车型车道分配规律等交通流数据,后者可与前述车辆数据共同组成反映实际运营状态的车流数据[2].
目前,采用特定地点的实测车流数据被视作桥梁车辆荷载研究的发展趋势,而基于短期车流数据的荷载效应极值预测是其主流方法[3-4].国外学者开展的研究,多通过动态称重(WIM)系统采集短期的实测车流数据,在其基础上运用不同方法预测荷载效应极值[5-7].然而,我国现阶段的实际情况是:收费站的静态车辆数据以及高速公路的交通流数据相比于WIM车流数据更为充足.因此,若能将静态的车辆数据与交通流数据合成为模拟车流(以下简称合成车流),则可以方便地利用现有数据建立符合实际运营状态的车辆荷载模型.
Rice[8]提出了基于短周期数据外推长回归期极值的数学方法,该方法要求外推数据满足平稳高斯过程,Ditlevsen已经证明大跨径桥梁的实测车辆荷载满足这一假定[9].如果考虑运用Rice公式方法进行合成车流作用下的荷载效应极值预测,则需首先证明该方法对于合成车流数据的适用性,即合成车流作用下的荷载也满足平稳高斯过程.
以下将首先建立基于静态称重数据合成车流的方法,介绍应用Rice公式进行车辆荷载效应极值的预测方法,证明了该方法对合成车流的适用性;通过算例验证了合成车流荷载效应及其预测极值的准确性,并简要对比了现有规范与本文方法在车辆荷载效应方面的差异.
1 基于合成车流的车辆荷载效应模拟
1.1 车辆特性与交通流特性的数学模型
为准确模拟指定区域的车辆荷载效应,应对桥上运营车辆进行车型划分[2],具体的划分标准应依据不同车辆的尺寸、轴距、车重等建立.研究中将高速公路车辆按轴数及车重划分为11类,在此基础上可根据实测的车辆和交通流统计数据,建立实际车辆荷载特征相对应的数学模型.对于合成车流模拟,车辆特性模型主要包括车型比例、车重、车长、轴重、轴距等参数.其中,对于桥梁跨中弯矩、斜拉桥拉索以及悬索桥主缆缆力等常规问题,车辆特性模型中需明确不同车型的车重、车长特征;而对于斜拉索、吊杆以及桥面板疲劳等特殊问题,还需进一步明确相应的轴重、轴距特征.现有大量的收费站静态数据可为各地区的桥梁荷载研究提供充足的车辆特性数据.经实测数据校验,车长、轴距相对稳定,可在模拟中作为常数参量,而车重、轴重变量一般服从正态分布.图1为第6类车实测车重的概率分布拟合结果,其余车型的拟合结果与之类似.
除车辆特性模型外,基于合成车流的荷载效应模拟还需建立交通流特性模型,主要包括车速、车型车道分配规律等内容.相关数据可根据桥址区域的高速公路交通流调查统计得到.例如,针对2008年广东省某高速公路的统计表明,不同车型的车速变量服从均值65.49到80.46的正态分布.图2为第6类车实测车速的概率分布拟合结果,其余车型的拟合结果与之类似.
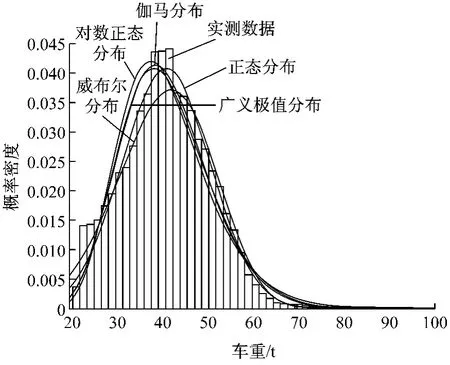
图1 第6类车实测车重的概率分布拟合Fig.1 Gross weight distribution of Class 6

图2 第6类车实测车速的概率分布拟合Fig.2 Speed distribution of Class 6
1.2 车辆到达与交通事故模型
建立合成车流所需的车辆特性、交通流特性模型后,可利用Monte Carlo方法模拟产生与实测数据具有相同规律的车辆荷载流[10].车流模拟过程中还需建立车辆到达与交通事故模型.
首先,在指定交通流量q下,应根据一定时间内到达的汽车数量为参数建立车辆到达模型.当车流密度不大、车辆间的相互影响微弱时,常用泊松分布模拟指定时间间隔t内到达k辆车的概率P(k):
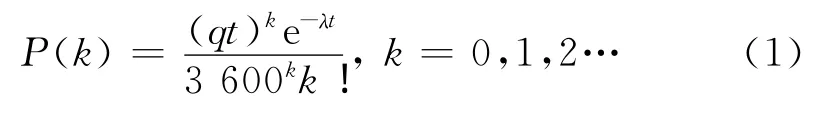
式中:q为交通流量,辆为时间间隔t内的平均到达率.
相应地,当车流密度较大、车辆在车队内自由行驶得不方便时,宜采用二项分布:
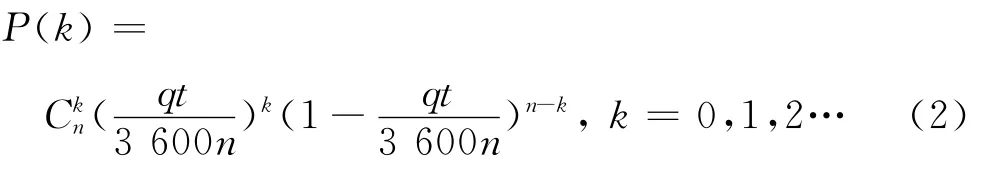
式中n为正整数.国内外现有研究普遍采用泊松分布建立所需的车辆荷载模型.
其次,模拟中可根据交通事故的发生率与交通流量的相关性[11],考虑车辆运行过程中可能发生的交通事故,以及由事故所引发的拥堵等不利工况对结构的影响:

式中:m为某一时期内某类事故发生次数;α,β,γ为参数.通过在模拟中重现桥梁运营期内任何可能发生的事故场景,弥补了单纯基于动态称重系统的短期实测数据对于某些不利车辆荷载工况的统计缺失[2]
1.3 合成车流及其荷载效应时程
在指定交通流量下,通过车辆到达模型可产生模拟时间步内到达桥梁的车辆数.之后根据车辆特性模型分配车辆类型以及车重、车长等参数,并基于交通流特性模型进行车道选择,赋予车速等信息,合成桥梁正常运营状态下的车辆荷载流.同时基于交通事故模型,可以确定不同类型事故的发生概率以及由此导致的不利工况影响,从而模拟事故状态下的合成车辆荷载流.
在此基础上,可选用基于影响面的叠加原理或有限元直接加载两种方式,计算由合成车流产生的荷载效应,最终实现指定区域实际运营状态下的车流荷载效应模拟,适应不同区域桥梁的特殊需求[10].具体流程如图3所示.

图3 基于合成车流的荷载效应模拟流程Fig.3 Process of live load effect simulation and extrapolation based on synthetic vehicle flow
2 基于合成车流的车辆荷载效应极值预测
2.1 基于Rice公式的荷载效应极值预测方法
对于大跨径桥梁,描述荷载效应(如应力、应变、弯矩等)时间变化的随机过程X常被视作平稳高斯过程[9],部分中小跨径桥梁的车辆荷载效应亦被证明服从这一假定[12].对于满足平稳高斯过程的荷载效应,可根据相应的时程曲线绘制水平穿越次数(频次)直方图,其穿越次数v(x)应满足式(4)所示的Rice公式[8],这一特点可以用于推断任意重现期内的荷载效应最大(小)值:
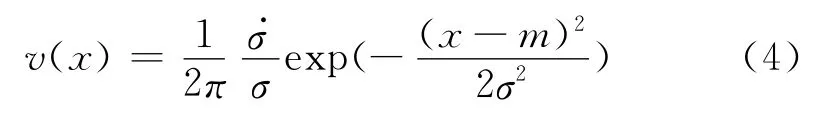
式中:σ为随机过程X的标准差为随机过程导数的标准差;m为随机过程平均值.推定过程中,由于Rice公式中的各参数难以确定,于是对公式(4)取对数,则其可转化为
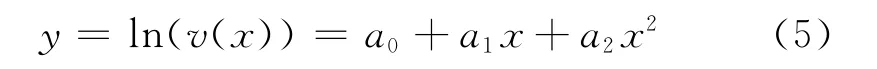
式中:a0=lnv0-m2/2σ2,a1=m/σ2,a2=-1/2σ2.
Cremona在文献[4,7]中详细论述了基于Rice公式的极值预测方法,指出经统计检验确定水平穿越次数(频次)直方图的最优的拟合起点值xopt之后,不同重现期Rt内的荷载效应最大值xmax(Rt)可计算如下:
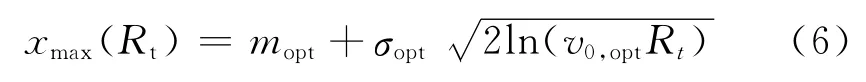
式中:平均值mopt、标准差σopt以及变量v0,opt均与直方图的最优拟合起点值xopt相对应,可根据式(5)计算得到的.重现期Rt可表示为基准期Tref及超越概率α的函数,即:

2.2 合成车流数据对于Rice公式极值预测方法的适用性检验
运用Rice公式进行极值预测的前提是车辆荷载效应须满足平稳高斯过程的假定[8].因此对于合成车流作用下的极值预测,关键问题是证明相应荷载效应服从平稳高斯过程.
首先,需证明合成车流作用下的荷载效应为平稳随机过程.作为大样本下统计推断的基础,平稳随机过程的统计特征不随时间变化,一般常采用单位根检验来判断随机过程是否平稳[13],相关推导过程如下:
已知白噪声ut为平稳随机序列,在此基础上非平稳的随机游走序列Xi可表示为

式(8)可视作随机模型Xt=ρXt-1+ut中参数ρ=1的特殊情形,称为存在单位根.经变形、简化后可得:
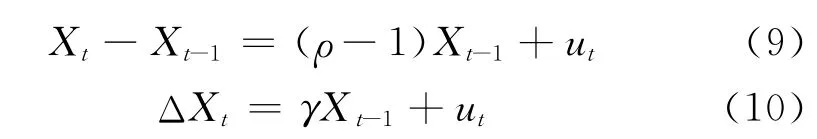
式中:参数γ=ρ-1.易知此时零假设H0:γ=0表示时间序列Xt存在单位根,随机过程是不平稳的;相对的假设H1:γ<0表示时间序列Xt不存在单位根,随机过程是平稳的.
Dickey和Fuller提出可以通过计算DF(Dickey-Fuller)统计量进行单位根检验,该方法又被称作DF检验.即当DF统计量小于临界值时,随机过程Xt拒绝零假设H0:γ=0,可以认为Xt具有平稳性.其中,DF统计量可表达为以下形式:
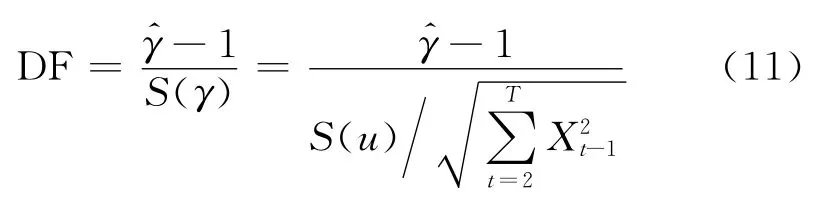
为保证随机误差项的白噪声特性,Dickey和Fuller在式(10)的基础上对DF检验方法进行补充,最终形成了改进的DF检验方法(ADF检验):
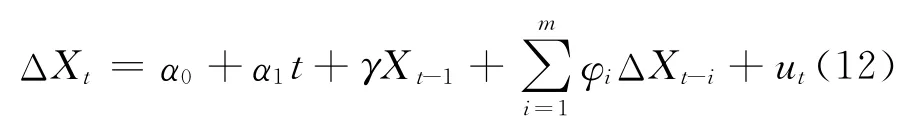
式中:α0为常数项,α1t为趋势项为 ΔXt的滞后项,其中 ΔXt-i=Xt-i-Xt-i-1.
这里通过ADF方法检验合成车流数据的平稳性,即利用式(11)—(12)证明合成车流作用下的荷载效应时程不存在单位根(拒绝H0假设).为保证研究结论的可靠性,分别生成不同跨径桥梁在高、低两种交通流量下的10组合成车流荷载效应数据,之后采用ADF方法逐一进行平稳性检验,同时通过t检验方法校验统计结果.检验结果表明,各组荷载效应时程都能够拒绝H0假设,且保证率均超过99.99%.因此,合成车流作用下的车辆荷载效应满足平稳随机过程的假定.
其次,为利用Rice公式方法预测合成车流的荷载效应极值,除平稳随机过程外,还需进一步证明合成车流作用下的荷载效应服从高斯分布.因此,对前述10组合成车流的荷载效应数据进行统计分析,绘制相应的概率分布直方图,按高斯分布对直方图进行拟合,并通过K-S检验法校验拟合结果(归一化后如图4-5所示).校验结果表明,在多组合成车流作用下,不同结构的荷载效应均服从高斯分布.
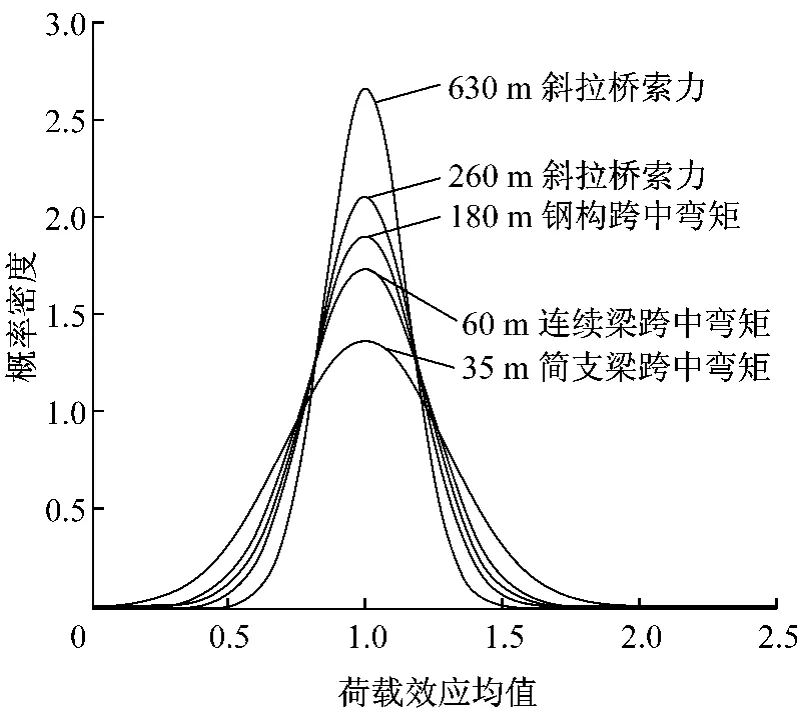
图4 低流量下合成车流荷载效应的高斯分布拟合Fig.4 Gaussian distribution of live load effect based on synthetic vehicle flow in low traffic volume
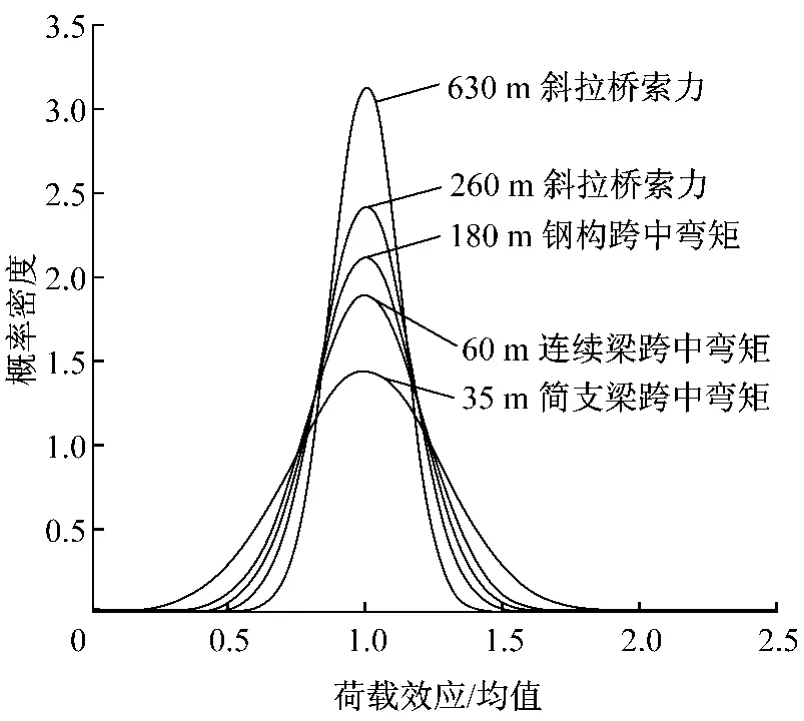
图5 高流量下合成车辆荷载效应的高斯分布拟合Fig.5 Gaussian distribution of live load effect based on synthetic vehicle flow in high traffic volume
以上研究结果表明,基于合成车流的车辆荷载效应服从平稳高斯假定,因此可利用Rice公式方法预测合成车流的荷载效应极值.
3 算例
为阐述基于合成车流的车辆荷载效应模拟及其极值预测方法,下面给出了一个具体算例.已知斜拉桥的拉索应力与其上车辆的运营状态密切相关,因此对于不同斜拉桥的活载附加索力,理论上应根据桥址区域的车辆荷载水平进行具体分析.本文以某主跨730 m的双塔斜拉桥为例,研究合成车流模拟方法的准确性,并利用Rice公式方法计算合成车流作用下跨中斜拉索的活载附加应力极值,将其与极值理论的计算结果以及现有规范的荷载效应水平进行对比.
首先,利用前述合成车流模拟方法生成短期荷载效应,并对其准确性进行校验.通过动态称重WIM系统采集了桥址附近的实际车流数据,计算得到相应的跨中斜拉索应力时程.同时,将该WIM车流做静态化处理,提取车辆及交通流特性数据,生成桥跨范围指定时间域(3周)内的荷载效应时程.将合成车流与实测数据进行比较(图6)后发现,合成车流能够很好地反映车重、车速、车型比例等基本的车流特性,对于荷载效应,合成车流与实测值的均值、方差均较接近,但极值稍高,这主要是由于合成车流比短期实测数据更加全面地考虑了运营期内可能出现的各种极端不利工况.
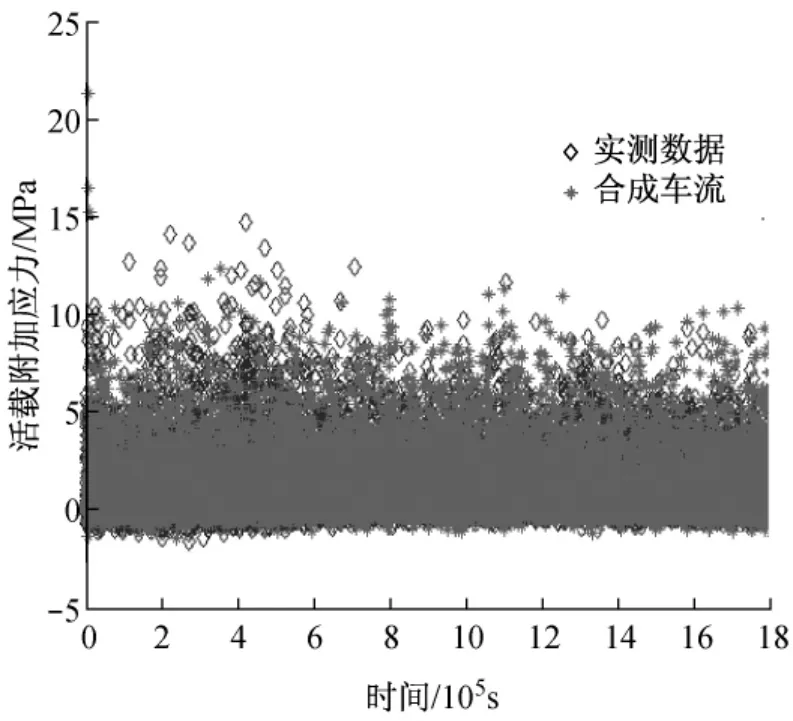
图6 实测与合成车流的荷载效应比较Fig.6 Effect of WIM and synthetic vehicle flow
其次,对基于合成车流产生的短周期车辆荷载效应数据进行外推,预测并校验长寿命周期内的荷载效应最大值.根据3周的模拟荷载效应样本,绘制得到如图7所示的水平穿越频次直方图,依据式(6)—(7)可计算不同重现期及对应基准期内的效应极值.同时,根据极值理论[14]计算跨中斜拉索附加应力的理论极值,将其与Rice公式的计算结果进行对比(图8).对比结果表明,不同重现期下Rice外推极值与理论极值基本吻合.此外,如图8所示,在现有的实际车辆荷载水平下,合成车流于基准期100年内产生的跨中斜拉索最大附加应力为46.5 MPa(对应重现期为1950年一遇),小于按现有规范计算得到的车辆荷载附加应力51.1 MPa.

图7 穿越频次直方图拟合Fig.7 Outcrossing rate histogram fitting
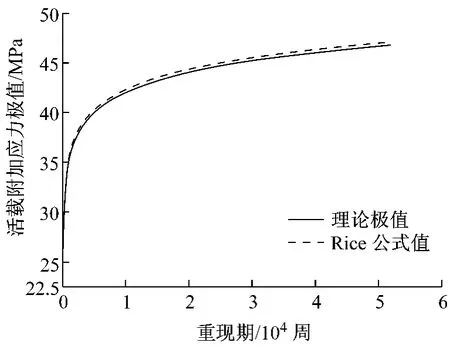
图8 Rice公式预测极值检验Fig.8 Test of Rice formula extrapolation
4 结论
本文利用我国现阶段已有的大量收费站静态车辆数据以及高速公路的交通流数据,研究车辆特性、交通流特性以及车辆到达和交通事故等的数学模型,提出并建立了基于合成车流的车辆荷载效应模拟方法,可合成短期车流并生成相应的荷载效应时程,建立符合实际运营状态的车辆荷载模型.同时证明了合成车流作用下的荷载效满足平稳高斯过程,从而验证了Rice公式方法对于合成车流荷载效应极值预测的适用性,可在此基础上实现长重现期内的结构安全评价.研究通过算例校验了合成车流作用下荷载效应及其预测极值的准确性,并简要对比了与现有规范计算结果的差异.
[1] Getachew A,O’Brien E J.Simplifed site-specific traffic load models for bridge assessment[J].Structure and Infrastructure Engineering,2007,3(4):303.
[2] O’Connor A,O’Brien E J.Traffic load modelling and factors influencing the accuracy of predicted extremes[J].Canadian Journal of Civil Engineering,2005,32(1):270.
[3] Nowak A S.Live load model for highway bridges [J].Structural Safety,1993,13(1+2):53.
[4] Cremona C.Optimal extrapolation of traffic load effects[J].Structural Safety,2001,23(1):31.
[5] Getachew A.Traffic load effect on bridges[D].Stockholm:Royal Institute of Technology Stockholm,Structural Engineering,2003.
[6] Ghosn M,Sivakumar B,Moses F.Modeling maximum live load effects on highway bridges[C]//Proceedings of the 1st International Symposium on Life-cycle Civil Engineering.Varenna,Lake Como:Taylor &Francis,2008:335-341.
[7] Cremona C.Probabilistic approach for cable residual strength assessment[J].Engineering Structures,2003,25(3):377.
[8] Rice S O.Mathematical analysis of random noise[C]//Selected Papers in Noise and Stochastic Processes.New York:[s.n.],1954:133-141.
[9] Ditlevsen O.Traffic loads on large bridges modeled as white noise fields [J].ASCE Journal of Engineering Mechanics,1994,120(4):681.
[10] Crespo-Minguillón C,Casas J R.A comprehensive traffic load model for bridge safety checking[J].Structural Safety,1997,19(4):339.
[11] 巴布可夫.道路条件与交通安全[M].景天然译.上海:同济大学出版社,1990.Bobokov B Ф.Road conditions and traffic safety[M].Translated by JING Tanran.Shanghai:Tongji University Press,1990.
[12] Jacob B.Methods for the prediction of extreme vehicular loads and load effects on bridge [R].WG8 report,Eurocode 1:Traffic Loads on Bridges.Luxembourg:Office for Official Publications of the European Communities,1991.
[13] 古扎拉蒂,波特.计量经济学基础[M].第5版.费剑平译.北京:中国人民大学出版社,2011.Gujarati D N,Porter D C.Basic of econometrics[M].5th ed.Translated by FEi Jianping.Beijing:China Renmin University Press,2011.
[14] Fu G K,You J.Extrapolation for future maximum load statistics[J].Journal of Bridge Engineering,2011,16(4):527.
