大口径主镜轻量化结构参数的优化设计

叶伟楠，董吉洪

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033;2.中国科学院 研究生院，北京100039)

1 引 言

在空间相机中，主镜不仅直接决定空间相机的光学性能，而且关系到空间相机的力学特性、热稳定性以及相机的制造难度和成本［1］。由于主镜设计的重要性，国内外的科研工作者为此倾注了大量精力。欧美先进国家已经能够制备口径＞2 m的主镜［2］，而国内由于起步相对较晚，虽然也取得了一定的成果，但是相关研究都是针对口径为250 ～1 000 mm 的主镜［3-5］。对于更大口径的主镜，由于镜体重量、支撑结构及加工工艺等诸多因素的限制，难以达到镜面面形精度的要求。为了提高主镜的各方面性能，主镜的轻量化设计是一个重要途径。由于运载火箭能力以及航天器制造难度和成本等多方面的限制，航天器的有效载荷需要严格控制，所以减轻空间相机的主镜及其支撑组件的重量，能够降低发射的难度，提高升空的可行性。从另一个方面讲，做地面试验时主镜受重力影响会导致面形精度下降，因此较轻的主镜质量有利于降低重力的影响，减小支撑结构的设计难度。

主镜的轻量化设计主要包括结构设计和参数优化。结构设计主要是针对各种轻量化形式的对比和选择，而在选定了某种轻量化形式以后，则需要对主镜镜体的具体结构参数进行优化设计，以达到性能最佳、质量最轻等目的。目前，主镜轻量化结构参数的优化设计多采用拓扑优化法或有限元软件法［6］，但这些方法有较大的局限性，不能同时对主镜的支撑位置和结构尺寸等关键参数进行全局的优化设计。本文引入了基于Kriging 近似模型的多目标遗传优化方法，对2 m 口径SiC主镜的轻量化结构参数进行了全局优化设计。

2 Kriging 近似模型的多目标遗传优化方法

先考虑这样一个问题，如图1 所示，对于x∈［a，b］上的未知函数f(x) =y，可以通过检测的方法得到f(t) =T，t为［a，b］上的任意值。为了求得f(x) 在定义域内的最大或最小值，可以先检测出均匀分布于［a，b］上的M个输入值tn的输出值Tn，然后对M个样本点(tn，Tn) 用插值法求得函数FM(x) ，FM(x) 作为f(x) 的近似函数。只需求得FM(x) 的最大值FMmax(h) =H，然后将h带入f(x) ，得到f(h) =H'，比较H和H'，如果误差很小，则认为f(h) =H'为f(x) 的最大值; 如果误差较大，则把(h，H') 作为第M+1 个样本点求得新的插值函数FM+1(x) ，如此迭代下去，直到近似函数的最大值和原函数的检测值近似相等，就可以认为使得近似函数取得最大值的输入量同时使得原函数f(x) 取得了最大值，这是求单一输入输出量最优解的常用方法。

图1 f( x) 和其近似函数F( x)Fig.1 Curves of f( x) and its approximate function F( x)

上述求最优解的方法如果扩展到多个输入输出量的复杂情况，就可以总结步骤如下:

(1) 抽样，即随机或按一定规律抽出一定数量的样本点X，实际问题中的抽样通过Isight 进行试验设计来实现。样本点越多，分布越均匀，就越能准确地描述整个样本空间。样本空间可按照其样本点数量的有限性和无限性，分为有限样本空间和无限样本空间。譬如对0 ～10 间的数字抽样，如果数字无最小单位量，则0 ～10 间可以抽出无数个样本点，为无限样本空间。但是如果最小单位量为1，则样本点只有0 ～10 间的11 个整数，为有限样本空间。

(2) 检测或仿真分析，目的是得到样本输入量X的对应输出量Y。只有能够通过检测或仿真分析等手段得到对应输出量的问题才能用近似模型的方法求最优解。

(3) 建立近似模型，也就是用数学工具建立输入量集合X到输出量集合Y的映射。这个映射能近似地反映所求问题的输入输出量之间的关系。

(4) 求近似模型的最优解。根据建立映射所采用的数学模型，选择合理的求解算法，得到近似模型的最优解。

(5) 最优解可靠性的判断。通过检测或仿真分析等手段得到近似模型最优解输入量Xm的实际输出量Y'm，比较Y'm和Ym。对于有限样本空间问题，Y'm=Ym，则Y'm为可靠的最优解; 反之则不可靠，需要迭代重新求解。对于无限样本空间问题，Y'm≈Ym，则Y'm为可靠的最优解; 反之则不可靠，需要迭代重新求解。

(6) 迭代求最优解。如果近似模型的最优解被判断为不可靠，则需要把新样本点(Xm，Y'm) 加入到近似模型的建立中，修正近似模型的准确性。如此反复迭代修正，直到最优解判断为可靠为止。

图2 给出了求解方法的大致流程。

图2 近似模型方法寻优流程Fig.2 Optimization process of approximate model method

该优化思路具体到主镜的轻量化结构参数优化设计中，即通过试验设计和仿真分析建立近似模型，然后对近似模型进行优化求解，再采用迭代法修正近似模型的准确性以得到最佳的轻量化结构参数设计。

为了能够用数学模型准确地模拟实际问题，近似模型的建立方法十分重要。Kriging 模型是一种估计方差最小的无偏估计模型，它能够提供一种精确的插值，同时能够覆盖整个试验区域。与回归分析相比，Kriging 模型更具优势［7］，它常能够提供更好的全局预测。对于给定输入条件，能够确定输出值的仿真试验。对于全局的Kriging 模型，要求试验设计能够均匀地充满样本空间，传统的试验设计抽样往往存在点堆积的问题［8］，而拉丁超立方试验设计则是一种能相对均匀地填满整个试验区间的设计［9］，并且每个试验变量水平只使用一次。Kriging 模型的优化求解一般较为复杂，所以优化算法常常采用不受数学求导和连续性限制的遗传算法。遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定，具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则［10］。

3 2 m 口径SiC 主镜轻量化结构参数的优化设计

为了验证上述方法在主镜轻量化结构参数优化中的可行性，本文采用集成了拉丁超立方试验设计、Kriging 近似模型和多目标遗传算法( NSGA II) 的工程优化软件ISIGHT，以2 m 口径的SiC 材质卡塞格林光学系统主镜为例，对其轻量化结构参数进行了优化设计。

3.1 主镜的技术指标

主镜材质为SiC，口径为2 m，球面镜曲率半径为4 m，要求镜体质量＜250 kg，重力作用下，要求主镜面形精度PV≤0.1λ，RMS≤0.02λ，其中λ=632.8 nm。

3.2 主镜的基本结构设计

根据设计要求，SiC 主镜直径为2 000 mm，镜面曲率半径为4 000 mm。按卡塞格林光学系统的要求，主镜中心开孔孔径为400 mm。SiC 主镜采用背部封闭式的单拱形状，轻量化孔为三角形，背部面板直径取1 800 mm，拱形面加强筋厚度取10 mm。采用18 点的背部支撑，支撑孔径取80 mm。除上述已确定的设计参数，将主镜镜面厚度tf、背部面板厚度tb、中心厚h、筋板厚度tw、三角形轻量化孔边长l、支撑内圈半径R1和支撑外圈半径R2等7 个参数作为待定变量进行参数优化。主镜基本形状如图3 所示。

图3 主镜的基本形状Fig.3 Basic shape of the primary mirror

3.3 主镜轻量化结构参数的优化

主镜优化设计的目的是在某种特定的工况下寻求主镜镜面厚度tf、背部面板厚度tb、中心厚h、筋板厚度tw、三角形轻量化孔边长l、支撑内圈半径R1和支撑外圈半径R2等7 个设计变量的最佳组合，使得主镜在面形精度PV 和RMS 满足某预设指标的前提下质量m最小，或使得主镜在质量m小于某预设指标的前提下面形精度PV 和RMS最优。

依据前人的设计经验，主镜在水平放置的情况下受重力影响最大，面形精度最差［11］; 竖直放置的情况下受重力影响最小，面形精度最好。虽然空间相机实际工作在微重力环境下，主要受温度变化的影响，但是在空间遥感器发射升空前需要对相机做很多地面实验和检测，所以相机主镜必须具有承受1g重力的力学能力。为了模拟相机在轨工作的状态，在对主镜做地面实验和检测时通常采用竖直放置，因此在做单镜的设计分析时通常使重力场垂直于光轴方向［12］。

主镜的基本形状和仿真分析的工况作为优化模型的固有属性，相当于前文所举二维事例中的函数f(x) ，优化过程中不能更改。主镜的7 个参数相当于事例中的输入量x，主镜质量m、镜面面形精度PV 和RMS 相当于事例中的输出量y，需要通过仿真分析求得试验抽样输入量对应的输出量，然后建立近似模型，迭代求解。

为了提高求最优解的效率，主镜优化采用有限样本空间的方法。确定了7 个参数作为优化的输入量后，为了得到有限的样本空间，需要规定各个参数的取值区间和最小单位量。将各参数的取值区间均分为10 等分，各得到11 个样本点，0，1，2……10，然后对整体样本空间通过拉丁超立方试验设计进行样本数为20 的抽样。抽样后将参数样本进行CAD 建模，并利用仿真分析和面形参数拟合得到其质量和面形精度参数，20 个抽样的输入输出量对应关系如表1 所示。

表1 20 个抽样的输入输出量数据Tab．1 Input and output data of 20 samples

将表1 作为Database File 建立Kriging 近似模型。ISIGHT 计算出Kriging 插值系数后，能够预测样本空间内任意输入量对应的输出量，包括非抽样点，并且能在给定任意6 个输入量时，描述剩余单一输入量和任意输出量之间的函数关系。

按设计要求设定优化的边界条件质量m＜250 kg，面形精度: PV≤0.1λ，RMS≤0.02λ，目标函数为面形精度RMS 的最小值，采用NSGA-II 求近似模型在此边界条件和优化目标下的最优解。求出最优解后，由于Kriging 近似模型的准确性未知，所以不能就此认定近似模型的最优解为实际问题的最优解，需要进行最优解可靠性的判断。本次主镜的优化设计采用的是有限样本空间，所以判断最优解的可靠性时，首先需通过有限元仿真计算出输入量对应的实际输出量RMS＇，然后比较实际输出量RMS＇和预测输出量RMS，如果相等，可认为Kriging 近似模型在样本点附近准确性较高，求得的最优解可靠，可判定为实际问题的最优解。如果不相等则需要迭代修正近似模型的准确度，直至最优解可靠。

如表2 所示，经过5 次迭代后，主镜轻量化结构的参数达到了最优，其中质量m=243 kg，面形精度PV=25.7 nm，RMS=4.7 nm，均满足设计指标要求。表3 为最优解参数的实际数值。

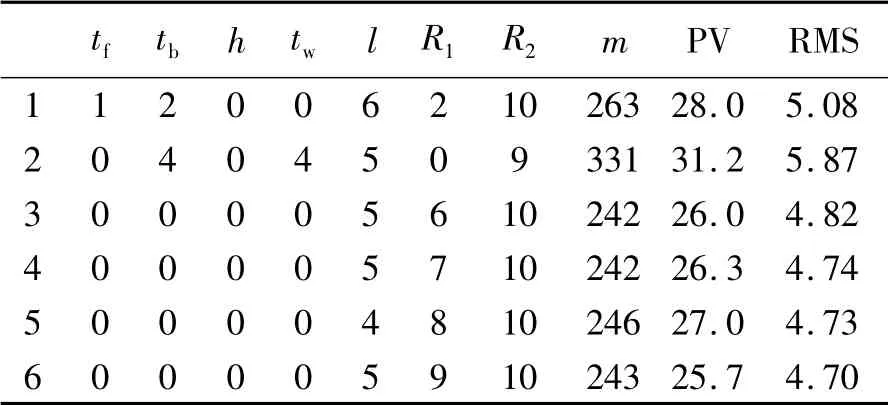
表2 迭代数据Tab．2 Iterative data

图4 为近似模型在最优解附近修正之后，各个参数对面形精度RMS 的影响曲线。

表3 最优解参数Tab．3 Optimal design parameters

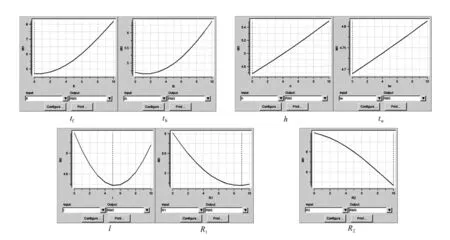
图4 各个参数对面形精度RMS 的影响曲线Fig.4 Influence curves of each parameter on surface accuracy

4 结 论

基于Kriging 近似模型的多目标遗传优化方法在航空、汽车、机械等领域应用广泛，但在光学系统的优化设计中却未见采用，故本文做了这方面的尝试。最终的优化结果显示: 此方法在主镜的轻量化结构参数优化设计中能有效地在边界条件范围内全局地优化多个参数，求得最优解。优化得到了质量为243 kg 的2 m 口径SiC 主镜，面形精度达到了25.7 nm PV，4.7 nm RMS，轻量化率达到了84%。

由此设想，将主镜设计的所有重要变量均参数化，如材料、主镜形状、轻量化孔形状等，甚至可以与支撑结构的主要设计参数共同进行统一的优化，寻求最优的配合，最终设计出各方面性能优异的主镜。不过随着优化参数的增加，要使近似模型更加准确地模拟实际问题，所需的样本数量也将增加，这必将带来巨大的工作量。

［1］ 刘宏伟.基于有限元法的空间相机主镜设计［D］.长春:中国科学院长春光学精密机械与物理研究所，2003.LIU H W. Design on the primary mirror of a space camera based on finite element method［D］. Changchun:Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，2003.( in Chinese)

［2］ ESPIARD J，TARREAU M，BERNIER J，et al.. SOFIA lightweighted primary mirror［J］.SPIE，1998，3352:354-365.

［3］ 韩媛媛，张宇民，韩杰才，等.碳化硅反射镜轻量化结构优化设计［J］.光电工程，2006，33(8) :123-126.HAN Y Y，ZHANG Y M，HAN J C，et al.. Optimum design of lightweight silicon carbide mirror［J］.Opto-Electronic Eng.，2006，33(8) :123-126.( in Chinese)

［4］ 张学军，李志来，张忠玉.基于SiC 材料的空间相机非球面反射镜结构设计［J］.红外与激光工程，2007，36(5) :577-581.ZHANG X J，LI ZH L，ZHANG ZH Y. Space telecope aspherical mirror structure design based on SiC material［J］.Infrared and Laser Eng.，2007，36(5) :577-581.( in Chinese)

［5］ 刘辉，于清华，裴云天.大口径反射镜轻量化结构比较及面形分析［J］.光电工程，2009，36(11) :70-74.LIU H，YU Q H，PEI Y T. Light-weighted structure contrast and deformation analysis of the large mirror［J］.Opto-Electronic Eng.，2009，36(11) :70-74.( in Chinese)

［6］ 杨佳文，黄巧林.大口径反射镜结构参数优化设计［J］.中国空间科学技术，2011(4) :77-83.YANG J W，HUANG Q L. Optimized design of structure parameters for large-aperture mirrors［J］.Chinese Space Science and Technology，2011(4) :77-83.( in Chinese)

［7］ VAN BEERS W C M，KLEIJNEN J P C . Kriging interpolation in simulation:a survey［C］//Simulation Conference 2004.Proceedings of the 2004 Winter Simulation Conference，Washington，USA，Dec 5-8，2004:107-115.

［8］ 张润楚，王兆军.关于计算机试验的设计理论和数据分析［J］.应用概率统计，1994(4) :420-435.ZHANG R CH，WANG ZH J. Design theory and data aanlysis of computer experiments［J］.Chinese J． Appl． Probability and Statisties，1994(4) :420-435.( in Chinese)

［9］ KJEIJNEN J P C. An overview of the design an analysis of simulation experiments for sensitivity analysis［J］.European J．Operational Res.，2005，164(2) :287-300.

［10］ 刘洪玉，胡成亮，赵震，等.多工位锻造工艺的多目标优化算法［J］.塑性工程学报，2010(3) :7-11.LIU H Y，HU CH L，ZHAO ZH，et al.. Multi-objective optimization algorithm of multi-station forging process［J］.J．Plasticity Eng.，2010(3) :7-11.( in Chinese)

［11］ 范磊，杨洪波，张景旭，等.2 m SiC 反射镜拱形轻量化结构设计［J］.光电工程，2010，37(10) :71-76.FAN L，YANG H B，ZHANG J X，et al.. Lightweight design for 2 m SiC arch mirror［J］.Opto-Electronic Eng.，2010，37(10) :71-76( in Chinese)

［12］ PARKS R E，WORTLEY R W，CANNON J E. Engineering with lightweight mirrors［J］.SPIE，1990，1236:735-743.