基于Zernike 模式的随机并行梯度下降算法的收敛速率
2012-10-30王卫兵王挺峰
王卫兵,赵 帅,郭 劲* ,王挺峰
(1.中国科学院 长春光学精密机械与物理研究所激光与物质相互作用国家重点实验室,吉林 长春130033;2.中国科学院 研究生院,北京100049)
1 引 言
波前畸变降低了激光光束质量,限制了激光的应用范围,但通过优化算法控制变形镜进行波前整形可改善光束质量。优化算法包括爬山算法、遗传算法、模拟退火算法和随机并行梯度下降( SPGD) 算法等[1],其中利用SPGD 算法进行波前整形是目前研究的热点之一。SPGD 算法利用性能指标测量值的变化量和控制参数的变化量进行控制参数的梯度估计,以迭代方式在梯度下降方向上进行优化控制参数搜索[2]。
1997 年,M. A. Vorontsov 等人将SPGD 算法成功应用在波前整形系统中[3],国内成都光电所姜文汉和李新阳课题组与国防科技大学刘泽金和梁永辉课题组在这方面也做了大量研究。在模拟仿真方面,文献[4]提到将Zernike 多项式用变形镜面形影响函数表示可得到最大的SPGD 算法收敛速率,但并未给出详细的结果; 文献[5]对随机并行梯度下降算法进行了较为详细的模拟仿真研究,获得了很好的理论结果,而且文献[5,6]均认为算法收敛速率在很大程度上依赖于参数的选取;文献[7]对基于Zernike 模式的SPGD 算法从描述波前的Zernike 阶数方面来研究算法的收敛速率和整形效果,提出了模式法和区域法结合的组合优化思想,但文献[2]指出仿真过程中性能指标测量模块的计算量是很耗时间的步骤; 文献[8]也指出由于采用迭代法导致收敛速率较慢的缺点还未得到解决,这限制了系统在动态环境中的应用。
为了进一步提高随机并行梯度下降算法的收敛速率,本文在SPGD 算法基础上进行理论分析,采用斯特列尔比作为系统性能评价函数,将波前和变形镜面形影响函数用同样的Zernike 多项式表示,从算法的形式上研究了算法的收敛速率和整形效果。利用Zernike 多项式的单位圆正交基性质,得到了两个常数矩阵,简化了算法的运算过程,加快了算法的运行时间;同时对算法的整形效果进行模拟仿真,获得了很好的结果,为实际的激光波前整形应用提供了理论指导。
2 仿真模型
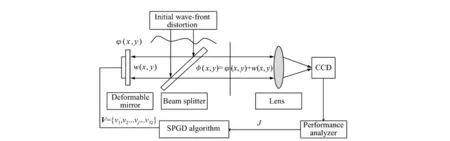
图1 波前整形系统Fig.1 Wave-front shaping system
如图1 所 示[2,5,7],波 前 整 形 系 统 工 作 原 理为:性能指标分析器根据CCD 采集到的数据计算性能指标J及其变化量ΔJ,随机并行优化算法根据变化量ΔJ得出32 单元变形镜控制电压矩阵V={v1,v2,……v32},并控制变形镜各驱动器来改变变形镜面形分布,然后由性能指标分析器计算校正相位后残余波前的性能指标J及其变化量ΔJ,以此循环迭代进行,直到满足算法停止条件为止。迭代过程的本质是: 在参数空间中寻找最佳变形镜控制电压矩阵Vbest={v1,v2,……v32},使得变形镜面形w(x,y) 生成一个趋于原始波前-φ(x,y) ,从而使残余波前φ(x,y) 最小,系统性能指标J趋于最优。
32 单元连续面型变形镜如图2 所示[5],面形函数为:
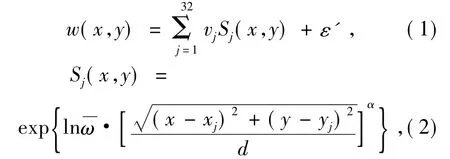
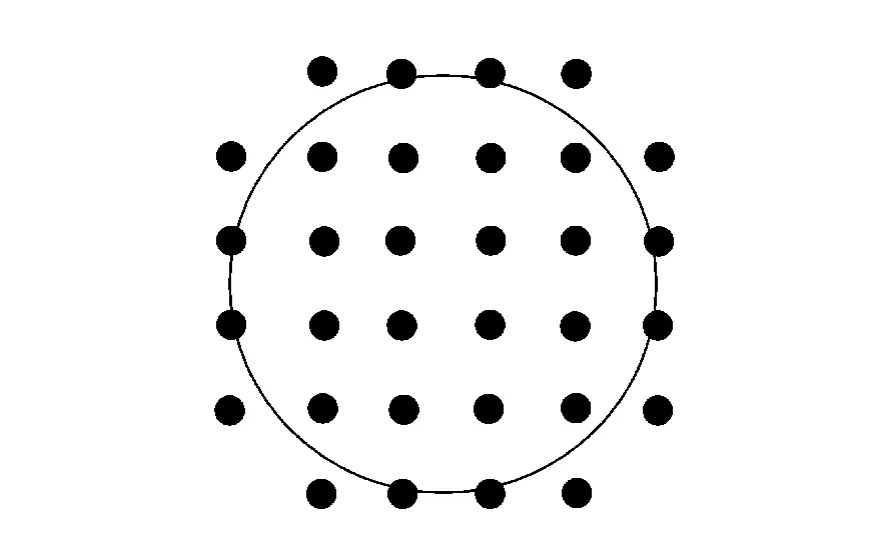
图2 32 单元变形镜Fig.2 32-unit deformable mirror
3 波前整形原理
3.1 性能指标
斯特列尔比(SR) 是一个通用的评价指标,是指实际畸变波远场光斑中心光强与理想平面波远场光强之比。根据物理光学,针对残余波前,可得到性能指标:
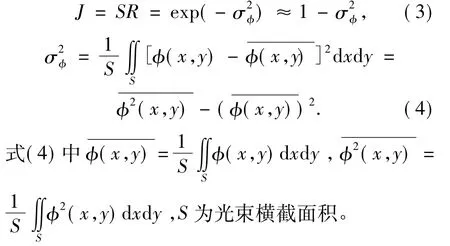
从式(3) 中可看出,波前相位方差σ2φ越大,或是波面起伏程度越大,SR越小,光束质量越差。所以,如果想得到接近理想的光波,那么就要减小波前相位方差σ2φ。
3.2 基于Zernike 模式的波前整形原理
文献[9]中前两项Zernike 像差分别为倾斜像差,可利用倾斜镜单独校正,所以选择第3 -14阶Zernike 多项式来表示初始静态畸变波前:
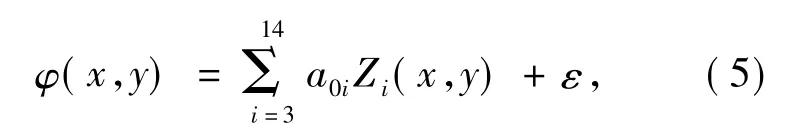
式中Zj(x,y) 表示第i项Zernike 多项式,a0i为相应项的系数,ε 为拟合残差,可忽略不计。
为了具有代表性并进行推广,将残余波前φ(x,y) 表示为:
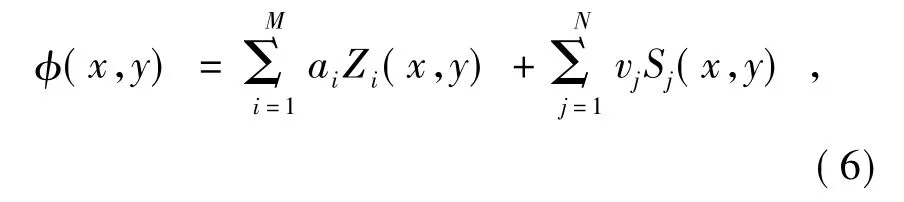
式中:M表示Zernike 多项式项数目,N表示变形镜驱动单元数目,表示前一次整形过程中的残余波前( 为后面处理方便,此处也用Zernike 多项式表示) ,此处的角标i从1 开始,只是形式上的需要,不影响表达意义。
对变形镜面形影响函数而言,可使用相同项数的Zernike 多项式进行拟合:
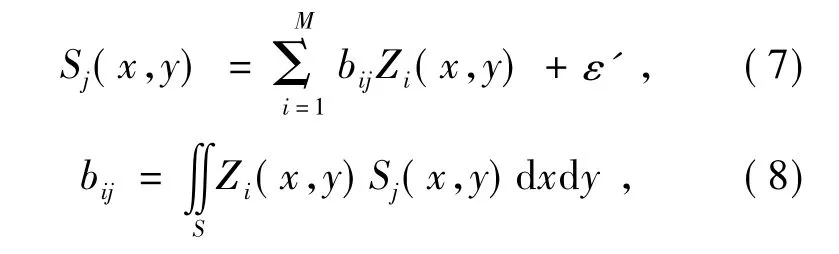
式中:ε'为拟合残差,可忽略不计,bij是变形镜面形影响函数Sj(x,y) 和Zernike 多项式Zi(x,y) 的常耦合系数,这是由于Sj(x,y) 和Zi(x,y) 都是提前确定的,所以可以构成一个常数耦合矩阵BM×N。
利用Zernike 多项式的单位正交性,采用矩阵形式,则式(3) 可进一步化简为:
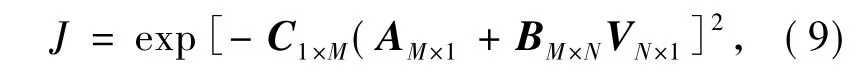
式(9) 中各矩阵表示为:

对静态畸变波前而言,式( 9) 中只有电压V变化,A、B、C 都是常数矩阵,因此积分计算便转化成了关于N个点的代数计算,从而迅速提升了算法的模拟运行时间。在上述模型中M=12,N=32。
3.3 随机并行梯度下降算法
SPGD 算法利用性能指标测量值的变化量和控制参数的变化量进行控制参数的梯度估计,以迭代方式在梯度下降方向上进行优化控制参数搜索[2]。双边SPGD 算法步骤[1]为:

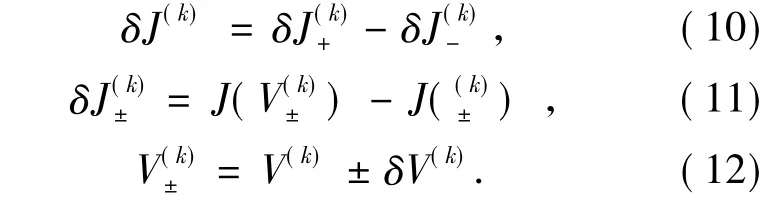
(5) 得到第k+1 次序列电压值为:
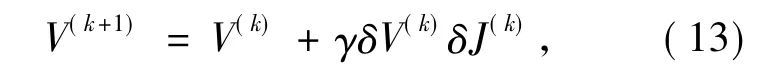
式中γ 为增益系数,可选择固定值,也可选择自动变化值,如[10]:
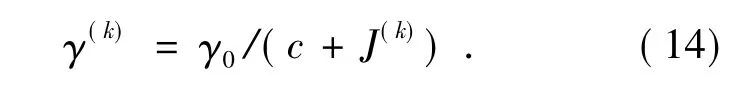
(6) 连续执行(2) ~(5) 步骤,直到满足算法停止条件为止,可以选择迭代次数或性能指标值作为停止条件,以下选择性能指标值作为停止条件。
4 仿真结果
随机产生的初始畸变波前分布如4.2 节的图3( a) 所示,性能指标为J=0.024 8,归一化衍射光强分布如图4( a) 和( e) 所示。利用图1 的波前系统,在处理器“Pentium ( R) Dual-Core CPU E5300@2.60GHz 2.62 GHz”和操作系统为32 位的计算机中通过Matlab7.8.0 对上述模型进行模拟,分别对6 种SPGD 算法的收敛速率做了对比,并对间接固定双边SPGD 算法的整形效果进行了模拟仿真。
4.1 6 种SPGD 算法比较
选择固定增益γ =0.15,算法停止条件J≤0.3,连续运行20 次,n代表运行试验次数,i、J、t分别代表校正到一定程度时的迭代次数、性能评价指标、算法运行时间和迭代频率代表相应的平均值,表示平均迭代频率。下面6 种SPGD 算法中( 可以组合出8 种SPGD 算法) 间接算法指式( 9) 中简化的代数点运算,直接算法指未简化的积分运算; 固定增益算法指采用固定增益系数,自动增益算法指采用自动变化增益系数;双边算法指同时采用V(k)+和V(k)-,单边算法指只采用V(k)+或V(k)-。
4.1.1 固定增益双边SPGD 直接与间接算法比较
(1) 间接算法
连续运行20 次结果如表1 所示,相应的平均值为:
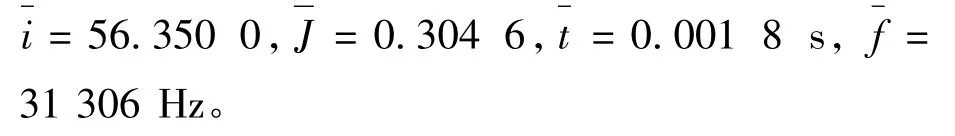
(2) 直接算法
连续运行20 次结果如表2 所示,相应的平均值为:
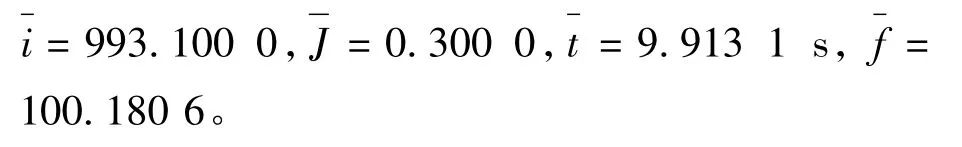
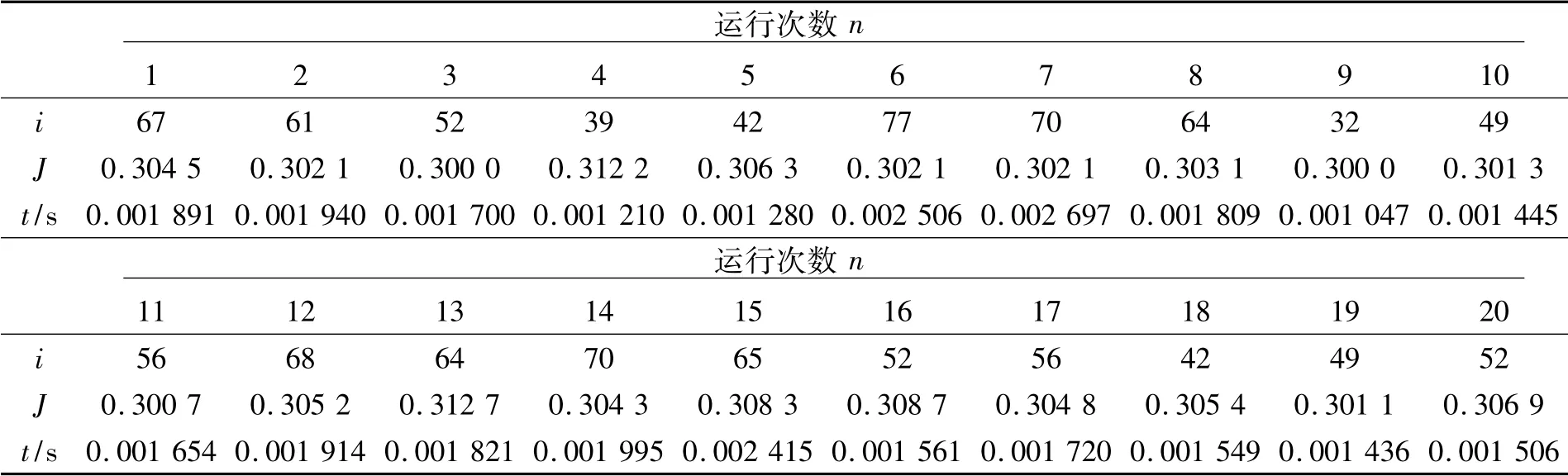
表1 连续运行20 次间接算法得到的结果Tab.1 Results of running indirect algorithm 20 times continuously
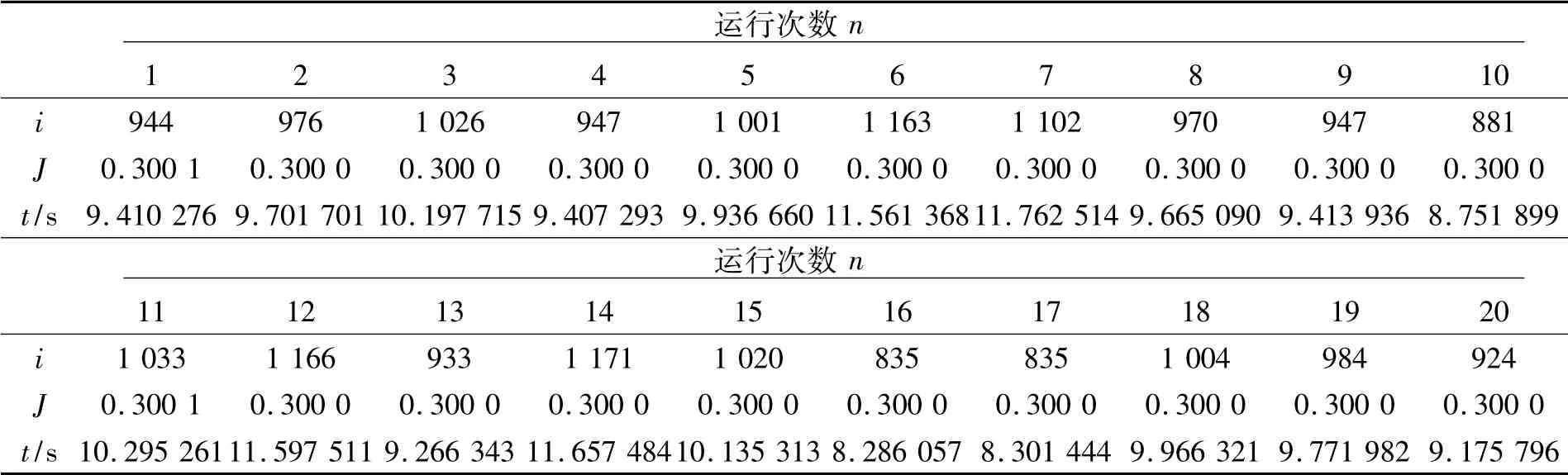
表2 连续运行20 次直接算法得到的结果Tab.2 Results of running direct algorithm 20 times continuously
(3) 结果分析
同样条件下,从迭代次数上看,间接算法要比直接算法快近乎17 倍,从运行时间上看,间接算法要比直接算法快近乎5 507 倍,从迭代频率上看,间接算法要比直接算法快300 倍。所以不论用什么来评价,间接算法都要优于直接算法。
4.1.2 间接双边SPGD 固定增益与自动增益算法比较
固定增益系数选择γ = 0.15,自动增益系数[10]选择:
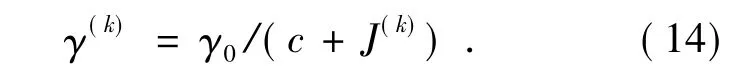
还有其它表达式[5],可看出这是个随J变大而减小的减函数,令c=0.001,J(0)=0.024 8 为初始畸变波前的SR,则γ0= γ(0)(c+J(k)) =0.003 9。
与上面类似,选择算法停止条件J≤0.3,连续运行20 次求平均值。
(1) 固定增益算法
同表1 结果相同,为:

(2) 自动增益算法
连续运行20 次结果如表3 所示,相应的平均值为:
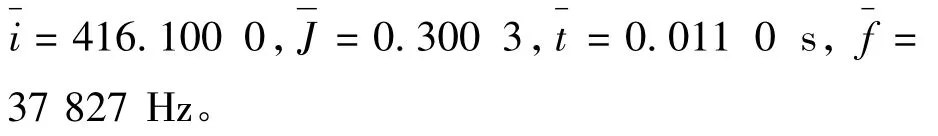
(3) 结果分析
同样条件下,虽然从迭代频率上看,自动增益算法要比固定增益算法快1.2 倍,但是从迭代次数上看,固定增益算法要比自动增益算法快近乎7 倍,从运行时间上看,固定增益算法也要比自动增益算法快近乎6 倍。采用迭代次数来衡量,固定增益算法也要好于自动增益算法。另外,由式(13) 可看出,对增益系数的改变将影响到扰动电压幅度值,所以可不考虑扰动电压幅度的影响。
4.1.3 间接固定增益SPGD 双边与单边算法比较
选择固定增益γ =0.15,算法停止条件J≤0.3,连续运行20 次求平均值。
(1) 双边算法
同表1 情况相同,为:
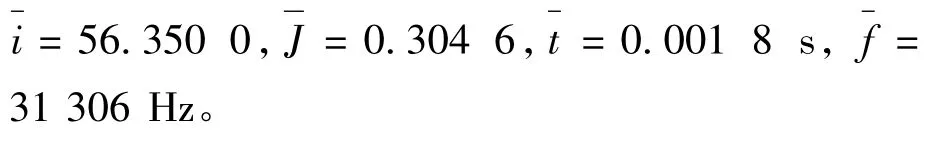
(2) 单边算法
连续运行20 次结果如表4 所示,相应的平均值为:

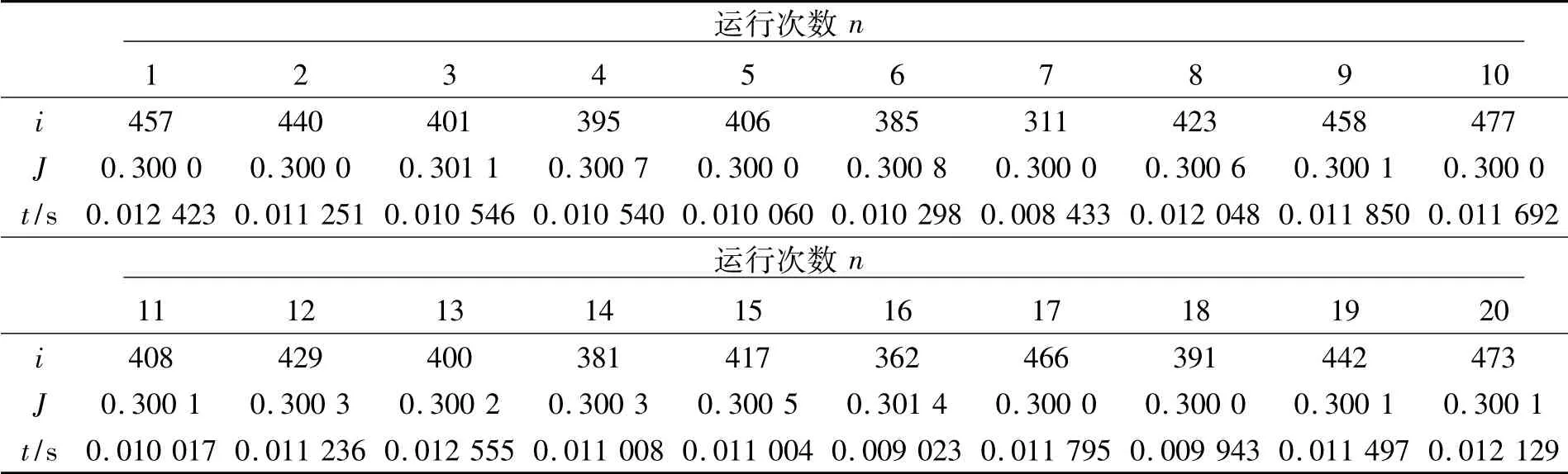
表3 连续运行20 次自动增益算法得到的结果Tab.3 Results of running automatic gain algorithm 20 times continuously
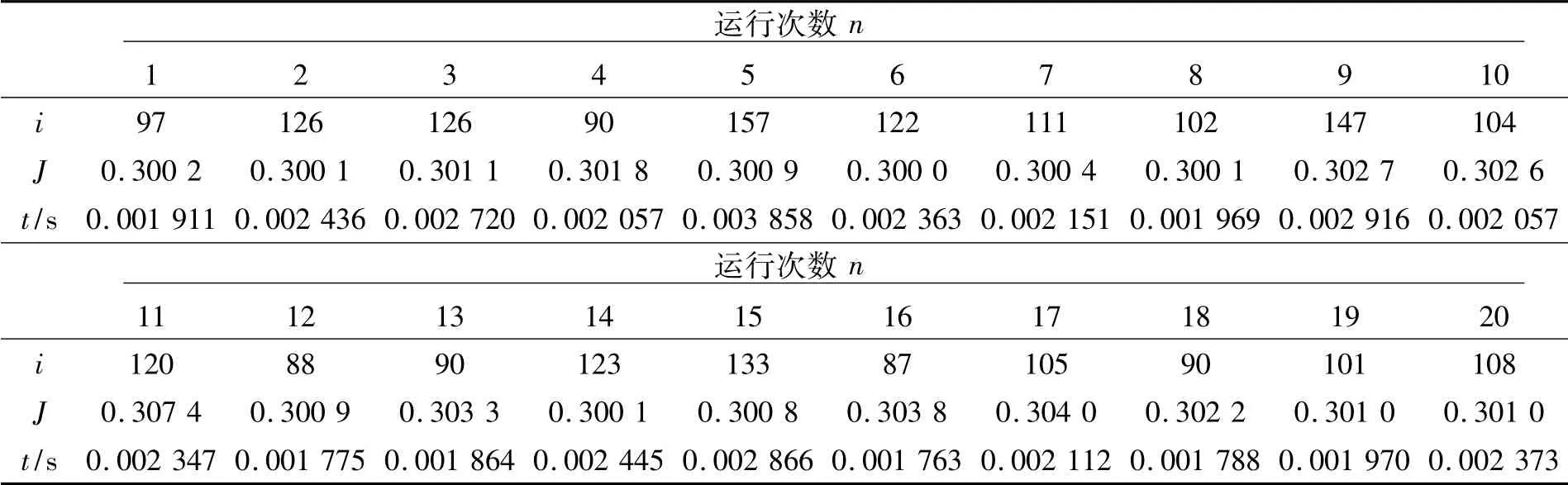
表4 连续运行20 次单边算法得到的结果Tab.4 Results of running unilateral algorithm 20 times continuously
(3) 结果分析
同样条件下,虽然从迭代频率上看,自动增益算法要比固定增益算法快1.5 倍,但是从迭代次数上看,双边算法要比单边算法快近乎20 倍,而且从运行时间上看,双边算法也要比单边算法快1.2 倍。采用迭代次数来衡量,双边算法要优于单边算法。这与文献[2]中的结论一致。但在实际波前整形系统中,一次迭代单边和双边SPGD算法分别需2 次和3 次测量性能指标[2],由于数据采集系统的时间消耗,双边SPGD 算法可能不及单边SPGD 算法实时性好。
综合上面3 对模拟结果,为了加快SPGD 算法收敛速率,在性能指标要求不高时,最佳算法为间接固定双边SPGD 算法; 在性能指标要求较高时,最佳算法为间接自动双边算法,这与文献[5]得到的结果相符。此外,上述的每组对比的运行条件只选择J≤0.3,若选择J≤0.8,那么对比效果就更明显了。近年来,为了进一步加快SPGD算法的收敛速率,文献[11-13]研制了基于硬件处理器的SPGD 控制器,并取得了良好的效果。
4.2 间接固定双边SPGD 算法的整形效果
上面只是将SPGD 算法进行到了J=0.3,为了进一步研究间接固定双边SPGD 算法的整体效果,选择运行条件为J≤0.8,同时为了加快收敛速率,此时取固定增益系数γ =6,其他条件不变,连续仿真50 次后结果为:平均完成一次静态波前畸变校正后,需要迭代次数i=660,校正时间t=0.015 4 s,性能评价指标J从0.024 8 提高到0.800 6,同时可求得迭代频率i=42 825 Hz。此时得到的波前分布和归一化衍射光强分布分别如图3、图4 所示。从图3 可看出,算法将初始畸变波前的PV =0.807 3λ,RMS =0.157 2λ 整形到PV=0.625 3λ,RMS =0.071 1λ,接近理想平面波前;从图4 可看出,整形后的光强分布向平面波前的光强分布( 服从贝塞尔函数分布形式) 逼近。以上结果表明间接固定双边SPGD 算法达到了波前整形的目的。
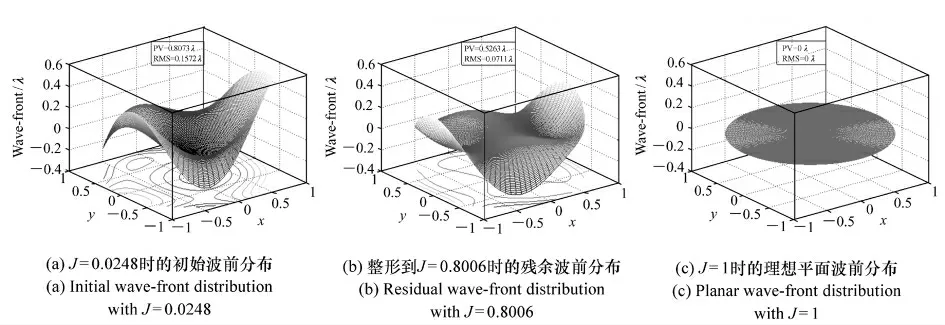
图3 利用间接固定双边SPGD 算法仿真的波前分布图Fig.3 Simulation of wave-front distribution using indirect-fixed-bilateral SPGD algorithm
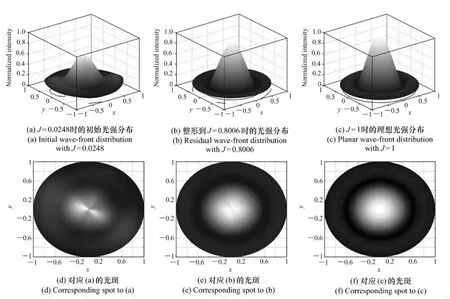
图4 利用间接固定双边SPGD 算法仿真的归一化衍射光强分布图Fig.4 Simulation of normalized diffraction intensity distribution using indirect-fixed-bilateral SPGD algorithm
5 结 论
本文对SPGD 算法进行波前整形的原理做了理论分析,基于Zernike 多项式的单位正交性质,利用同样的Zernike 多项式来拟合表示波前和变形镜面形影响函数,得到了两种常数矩阵B 和C,这种间接算法大大简化了算法的运算过程。这种处理过程也可应用在模拟退火算法和遗传算法中。对间接、直接、双边、单边、固定增益和自动增益组合的6 种SPGD 算法进行了3 组对比,结果发现,当性能指标要求不高时,可使用间接固定双边SPGD 算法来提高算法的收敛速率; 当性能指标要求较高时,应当使用间接自动双边SPGD 算法。对间接固定双边SPGD 算法的收敛速率和整形效果进行了仿真,收敛速率结果为:迭代660 次后可使波前的性能评价指标J从0.024 8 达到0.800 6;整形结果表明SPGD 算法可以达到波前整形目的,这些为激光整形提供了理论指导。
由于基于硬件处理器的SPGD 控制器[12-13]可实现高速波前相位控制,下一步的工作将重点围绕这种SPGD 控制器进行研究,并进行相应的实验验证。
[1] 王三宏.机并行梯度下降自适应光学技术在光束净化中的应用[D].长沙:国防科学技术大学,2009.WANG S H. Application of stochastic-parallel-gradient-descent adaptive optics techniques in beam cleanup[D]. Changsha:National University of Defense Technology,2009.( in Chinese)
[2] 杨慧珍,李新阳,姜文汉.自适应光学系统几种随机并行优化控制算法比较[J].强激光与粒子束,2008,20(1) :11-16.YANG H ZH,LI X Y,JIANG W H. Comparison of several stochastic parallel optimization control algorithms for adaptive optics system[J].High Power Laser and Particle Beams,2008,20(1) :11-16.( in Chinese)
[3] VORONTSOV M A,CARHART G W,RICKLIN J C. Adaptive phase-distortion correction based on parallel gradient-descent optimization[J].Opt. Lett.,1997,22(12) :907-909.
[4] VORONTSOV M A,SIVOKON V P. Stochastic parallel-gradient-descent technique for high-resolution[J].Opt. Soc. Am.A,1998,15(10) :2745-2758.
[5] 杨慧珍,李新阳,姜文汉. 自适应光学系统随机并行梯度下降控制算法仿真与分析[J]. 光学学报,2007,27( 8) :1355-1360.YANG H ZH,LI X Y,JIANG W H. Simulation and analysis of stochastic parallel gradient descent control algorithm for adaptive optics system[J].Acta Opt. Sinica,2007,27(28) :1355-1360.( in Chinese)
[6] 马慧敏,张鹏飞,张京会,等. 自适应光学系统随机并行梯度下降算法[J]. 强激光与粒子束,2010,22( 6) :1206-1210.MA H M,ZHANG P F,ZHANG J H,et al.. Stochastic parallel gradient descent algorithm for adaptive optics system[J].High Power Laser and ParticleE Beams,2010,22(6) :1206-1210.( in Chinese)
[7] 杨慧珍,李新阳.基于Zernike 模式的自适应光学系统随机并行梯度下降算法[J].强激光与粒子束,2009,21(5) :645-648.YANG H ZH,LI X Y. Stochastic parallel gradient descent algorithm for adaptive optics system based on Zernike mode[J].High Power Laser and ParticleE Beams,2009,21(5) :645-648. ( in Chinese)
[8] YANG H Z,LI X Y,GONG C L,et al.. Restoration of turbulence-degraded extended object using the stochastic parallel gradient descent algorithm: numerical simulation[J].Opt. Express,2009,19(5) :3052-3062.
[9] 李俊.传输型详查相机微小自适应光学系统研究[D].武汉:华中科技大学,2006.LI J. Study of the adaptive optic system in transmission type,high-resolution reconnaissance camera[D]. Wuhan: Huazhong University of Science and Technology,2006.( in Chinese)
[10] 王三宏,梁永辉,龙学军,等.随机并行梯度下降光束净化实验研究[J].光学学报,2008,28(4) :613-617.WANG S H,LIANG Y H,LONG X J,et al.. Experimental research of laser beam cleanup for dynamic aberrations based on stochastic parallel-gradient-descent method[J].Acta Opt. Sinica,2008,28(4) :613-617.( in Chinese)
[11] 王小林,周朴,马阎星,等.基于随机并行梯度下降算法光纤激光相干合成的高精度相位控制系统[J].物理学报,2010,59(2) :973-979.WANG X L,ZHOU P,MA Y X,et al.. High precision phase control system in conherent combining of fiber laser based on stochastic parallel gradient descent algorithm[J].Acta Physica Sinica,2010,59(2) :973-979.( in Chinese)
[12] 张金宝,陈波,王彩霞,等.61 单元自适应光学系统随机并行梯度下降算法动态实验研究[J].中国激光,2010,37(3) :668-674.ZHANG J B,CHEN B,WANG C X,et al.. Dynamical wave-front distortion correction experiment based on stochastic parallel gradient descent algorithm for 61-element adaptive optics system[J].Chinese J. Lasers,2011,37(3) :668-674.( in Chinese)
[13] 王彩霞,李梅,李新阳,等. 基于随机并行梯度下降算法的自适应光学实时并行处理机[J]. 光学学报,2010,30(11) :3076-3081.WANH C X,LI M,LI X Y,et al.. Real-time parallel wavefront processor for adaptive optics based on stochastic parallelgradient-descent algorithm[J].Acta Optica Simica,2010,30(11) :3076-3081.( in Chinese)
