由多个高斯函数表征的发光二极管光谱模型

谈 茜，饶 丰，张永林* ，徐何辰

(1.江苏科技大学，江苏 镇江212003;2.江苏检验检疫车辆灯具实验室，江苏 丹阳212300)

1 引 言

发光二极管( LED) 是半导体发光光源［1］，与传统光源相比，具有体积小、寿命长、光效高、光强稳定［2］、可智能控制［3］以及产品丰富等优点。LED 光谱是其光度色度特性研究的基础，目前对于LED 光谱的研究主要有两方面:一是研制先进的LED 光谱测量仪器;二是研究能准确描述LED光谱及其随条件变化的数学模型。LED 光谱模型对于光度色度测量仪器的研制、智能化LED 产品的设计具有重要的意义，因此受到国内外学者的关注。

2005 年，沈海平等人提出了一种描述LED 平均光谱的改进的高斯模型［4］，该模型将单色LED描述成对称的分布，但实际的LED 光谱是不对称的，同时该模型与实测光谱的误差较大。2010年，何国兴等人用分段函数建立不同驱动电流下LED 的光谱模型［5］，该模型较好地描述了LED 光谱的不对称性，但是精度不高，由于采用了分段函数，不便于应用。同年，朱继亦等人建立了修正的非对称的高斯分布模型［6］，该模型与实际光谱的相关指数R2在0.94 以上［7］，但该模型要事先判断光谱的不对称性，并输入一些参数，不利于自动化建模。更重要的是，已报道的这些模型均不能描述荧光粉转化LED 的光谱。

本文选用红、黄、蓝、绿和白色5 种LED 为研究对象，采用LED 光色电综合分析仪，测量不同驱动电流下LED 的光谱，提出了由多个高斯函数表征的一种新型LED 光谱模型。该模型对于n(n≥1) 个波峰的LED，选用3n个高斯函数来表示。采用额定电流下LED 的光谱计算模型系数，在求取其它电流下的光谱时，只需将峰值波长和半波宽换成相应电流下的值。为了验证该模型的准确性，分析了该模型与实测光谱之间的误差，并将该模型与已报道的模型进行比较。结果表明，本研究提出的模型不但精度较高、便于数据处理，而且结果具有普适性，有利于LED 的研究和应用。

2 实 验

采用的实验装置是杭州远方公司的LED 光色电综合测试系统，结构如图1 所示。数控高精度恒流电源给待测LED 提供电源，积分球、光谱计能够快速测量待测LED 的光谱分布并输入计算机存储和处理。

本实验选用驱动电流为20 mA 的红、黄、蓝、绿、白5 种颜色LED 各10 只，驱动电流为350 mA的红、黄、蓝、绿、白色LED 各10 只，共100 只作为研究对象。

图1 LED 光色电综合分析系统结构示意图Fig.1 Structure diagram of LED photometric，chromatic and electric characteristic analyzer

根据国家标准［8］，日常LED 灯具在额定电压和额定频率下稳定工作时，其实际消耗的功率与额定功率之差应不大于15%，因此，本研究测量了驱动电流为20 mA 的LED 在12 ～24 mA 下的光谱，测量间隔为2 mA，约为额定功率的60% ～120%;同时测量了驱动电流为350 mA 的LED 在300 ～400 mA 下的光谱，间隔为10 mA，约为额定功率的84% ～116%。测试环境温度为10 ℃。测试时采用脉冲点灯，并采用恒温器，以防止结温的影响［9］。

3 LED 光谱模型及误差分析

3.1 模型的提出

表1 给出了各单峰LED 由1 ～4 个高斯函数拟合的光谱曲线与实测光谱之间的误差平方和。从表中可以看出，1 个高斯函数拟合时，误差平方和较大，约为20%; 2 个高斯函数拟合时，蓝色LED 误差平方和超过5%;3 个高斯函数拟合时，误差平方和均在1%左右，而实验中使用的光谱仪重复测量的误差平方和为4%，测量误差占主导，拟合误差可以忽略;4 个高斯函数拟合时，测量误差仍是主要因素，降低拟合误差意义不大，同时，4 个高斯函数拟合时的表达式比3 个高斯函数复杂。因此，本研究对于单峰LED，其光谱F( λ) 用3 个高斯函数表示，如式(1) :

式中:A1i(i=1，2，3) 为各高斯函数所占的权重，a1i(i=1，2，3) 为系数，λp为LED 峰值波长，Δλ为半波光束角，m1i(i=1，2，3) 为光谱峰值波长修正系数，m11=0。

表1 误差平方和(SSE)Tab．1 Square sum of error(SSE)

荧光粉转换式LED 的光谱为双峰，经研究，其光谱F( λ) 可以采用式(2) 表示:

式中:A2j(j=1，2，3) 为各高斯函数所占的权重，a2j(j=1，2，3) 为系数，m2j(j=1，2，3) 为荧光粉峰值波长修正系数，λ＇p，Δλ＇为荧光粉峰值波长与荧光粉半峰光束角，m21=0。

3.2 多高斯模型系数寻优算法原理

对于n个峰值的LED 选择3n个高斯函数进行拟合，利用最小二乘原理［9］对系数求最优解。具体过程如下，残差f(xi) :

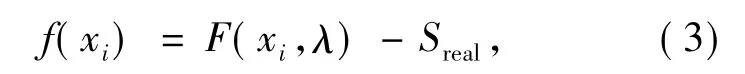
式中:F(xi，λ) 为光谱模型，xi为模型中的系数，即:xi=［A1i，A2j，a1i，a2j，m1i，m2j］(i=1，2，3;j=1，2，3) ，Sreal为实测光谱。残差f(xi) 的2-范数达到最小值的解即为最小二乘解，它可使总体误差较小。据此，将目标函数确定为:

式中:n为波峰的个数，λ 为波长。

计算该模型系数的最佳值实际上是一个多元函数无条件极值问题，极值问题的解通常是局部最优解，寻找全局最优解需要对局部最优解进行比较后得到［11］。求解优化问题的基本思想是用迭代法搜索最优解。迭代的第1 步是确定n维空间中的一点x0i的步长ε，以使到达下一点时，函数值f(xi) 下降，直至满足迭代终止条件。流程图如图2 所示。

图2 模型系数求解流程图Fig.2 Flow chart of calculating model coefficients

利用大、小功率LED 分别在额定电流为350和20 mA 时的光谱计算各颜色LED 的光谱模型的拟合系数，结果如表2 所示，表中m1j(j=1，2)有正有负，可见光谱具有不对称性，其值的大小可表示左右不对称的程度。

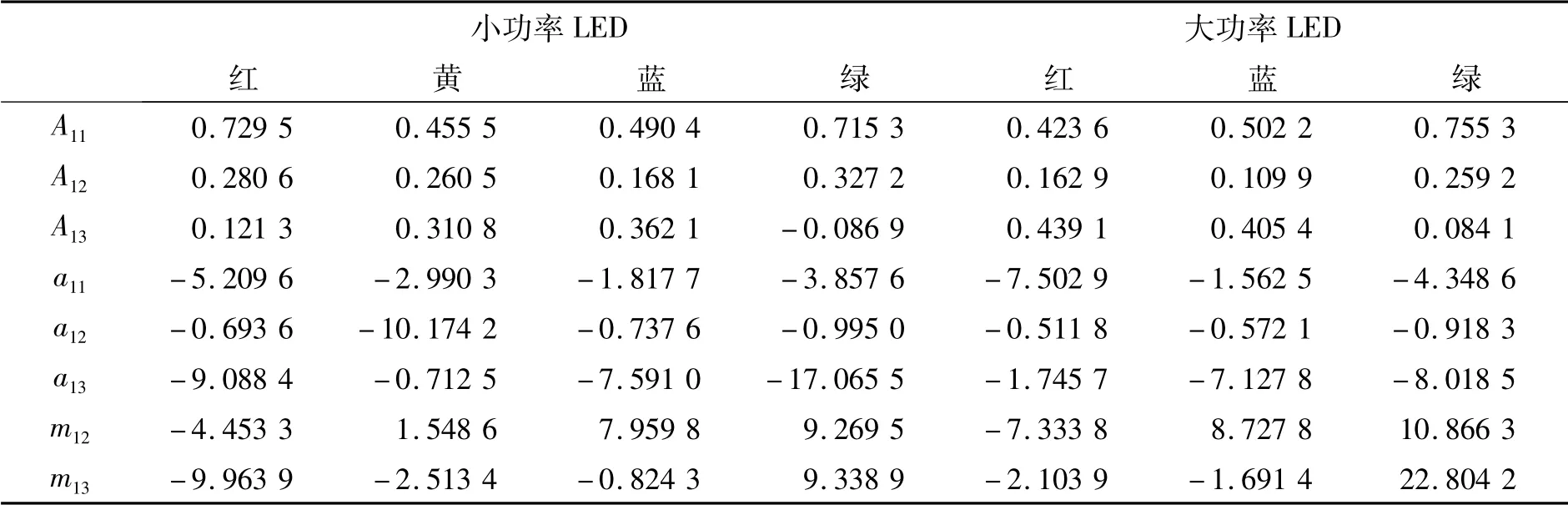
表2 单色LED 模型系数Tab．2 Model coefficients of monochrome LED

3.3 LED 的光谱模型与真实光谱之间的误差

研究中常用误差函数E来表征模型光谱与真实光谱之间的误差，如式(5) 所示:

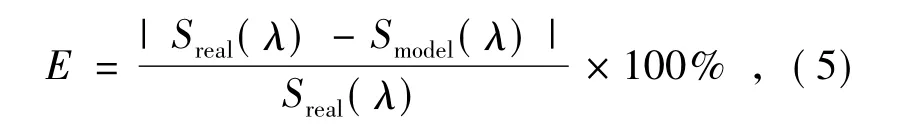
式中:Sreal( λ) 为实测LED 光谱，Smodel( λ) 为由模型求得的光谱。

图3 为各颜色大功率LED 光谱模型与实测光谱在300 ～400 mA 的平均误差，图中横坐标为电流，纵坐标为平均误差函数。由图可知，绿光的平均误差最大，约为4.65%，其它由大到小依次为红色，白色、蓝色和黄色，平均误差分别为3.45%、2.49%、2.33%、1.01%，黄色最小。

同理，图4 为各颜色小功率LED 光谱模型与实测光谱在12 ～24 mA 下的平均误差，由此可知各颜色光谱模型与实测光谱之间的误差由大到小依次为蓝色、绿色、黄色、红色和白色，其误差平均值分 别 为 3.77%、2.87%、2.65%、2.61%、2.48%。

3.4 多高斯组合模型与其它模型的比较

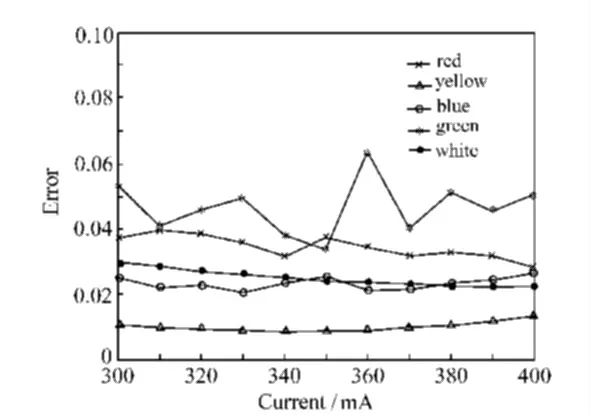
图3 大功率LED 模型与实测光谱之间的误差Fig.3 Error between the model of high power LED＇s spectrum and the measured one

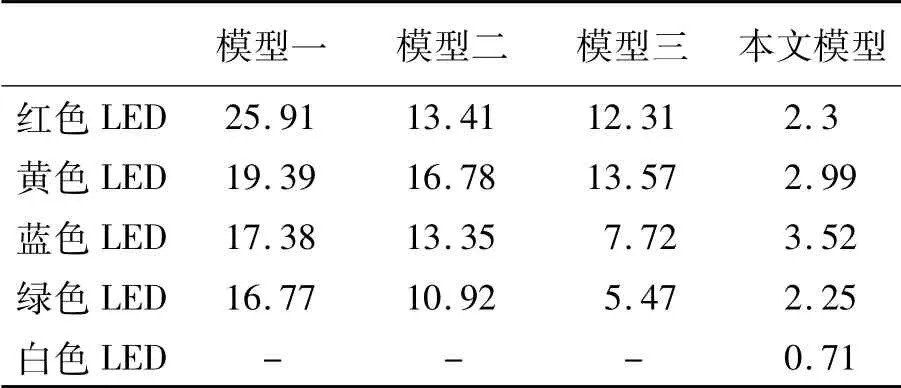
表3 小功率不同颜色LED 在各模型下的误差Tab．3 Error between the model and the measured spectrum of small power LED with different colors(%)

为了验证本文中模型的精度，将本文提出的模型与已经报道的3 个光谱模型进行了比较。为了表述方便，将沈海平、何国兴、朱继亦等人建立的模型分别称为模型一［4］、模型二［5］、模型三［6］，结果如表3 所示。由表3 可知，本文中提出的模型与实测光谱之间的误差均小于3%，而其它模型与真实光谱的误差一般在10%以上。因此，本文提出的模型较其它3 种模型的精度有了较大的提高。另外，模型一、二、三均未涉及白光光谱模型的研究，而本文给出了白光光谱模型，扩大了LED 光谱研究的范围，也说明本模型具有较好的普适性。

图4 小功率LED 模型与实测光谱之间的误差Fig.4 Error between the model of small power LED＇s spectrum and the measured one

4 结 论

利用LED 光色电综合测试系统测量了5 种颜色不同功率的LED 的光谱，并借助仿真软件对光谱进行了研究。提出了一种新型LED 光谱模型，并利用各颜色LED 在额定电流下的光谱计算模型中的系数，还将该模型与已报道的模型进行了对比。研究发现:对于n(n≥1) 个波峰的LED，可用3n个高斯函数形式的模型来表示，大功率红、黄、蓝、绿、白LED 的误差分别为3.45%、1.01%、2.33%、4.65%、2.49%; 小功率LED 的误差分别为2.61%、2.65%、3.77%、2.87%、2.48%。本模型可为光学仪器及智能化LED 产品的设计提供参考。

［1］ 周小丽，刘木清，钱勇，等.LED 光通量测试系统的研究［J］.光电子·激光，2008，19(6) :728-730.ZHOU X L，LIU M Q，QIAN Y，et al.. Study on the LED＇s total flux measurement system［J］.J． Optoelectronics Laser，2008，19(6) :728-730.( in Chinese)

［2］ 任健伟，麦镇强，万志，等.星上LED 定标光源的可行性研究［J］.光学 精密工程，2008，16(3) :398-405.REN J W，MAI ZH Q，WAN ZH，et al.. Feasibility of LED light source in spaceborne calibration［J］.Opt． Precision Eng．，2008，16(3) :398-405.( in Chinese)

［3］ 宋晓亮，苏来曼·艾，朱江，等.基于LED 的色度学实验研究［J］.大学物理实验，2011，24(5) :35-38.SONG X L，SU L M，ZHU J，et al.. Chromaticity experiments based on LEDs［J］.Physical Experiment of College，2011，24(5) :35-38.( in Chinese)

［4］ 沈海平，冯华君，潘建根，等.LED 光谱数学模型及其应用［C］.走进CIE26th-中国照明学会( 2005) 学术年会论文集. 北京:中国照明学会，2005:83-85.SHEN H P，FENG H J，PAN J G，et al.. Mathematical model for LED spectra and application［C］. About CIE 26th China Illuminating Engineering Society Annual Meeting Proceedings. Beijing: China Illuminating Engineering Society，2005:83-85.( in Chinese)

［5］ 何国兴，郑利红.不同驱动电流下LED 光谱模型［J］.中国光学快报，2010，8(11) :1090-1094.HE G X，ZHENG L H. A model for LED spectra at different drive currents［J］.Chinese Opt． Lett．，2010，8(11) :1090-1094.( in Chinese)

［6］ 朱继亦，任建伟，李葆勇，等.基于LED 的光谱可调光源的光谱分布合成［J］.发光学报，2010，31(6) :883-887.ZHU J Y，REN J W，LI B Y，et al.. Synthesis of spectral distribution for LED-based source with tunable spectra［J］.Chinese J． Luminescence，2010，31(6) :883-887.( in Chinese)

［7］ 何晓群，刘文卿.应用回归分析［M］.〛北京:中国人民大学出版社，2007.HE X Q，LIU W Q.Applied Regression Analysis［M］. Beijing:China Renmin University Press，2007.( in Chinese)

［8］ GB24823-2009.普通照明用LED 模块性能要求［S］.中国国家标准化管理委员会.北京:中国标准出版社:2010.GB24823-2009. LED modules for general lighting performance requirements［S］. Standardization Administration of the People＇s Republic of China. Beijing:China Standard Press，2010.( in Chinese)

［9］ 饶丰，葛志诚，朱金连，等.基于LED 光电参数之间关系的光效计算［J］.江西科学，2011，29(4) :424-427.RAO F，GE ZH CH，ZHU J L，et al.. The calculation of light efficiency based on the relationship among photoelectric parameters of LED［J］.Jiangxi Science，2011，29(4) :424-427.( in Chinese)

［10］ 王广斌，刘义伦，金晓宏，等.基于最小二乘原理的趋势项处理及其MATLAB 的实现［J］.有色设备，2005(5) :4-8.WANG G B，LIU Y L，JIN X H，et al.. Treatment of tendency part and its MATLAB accomplishment based on leastsquare principle［J］.Non-ferrous Metallurgical Equipment，2005(5) :4-8.( in Chinese)

［11］ 姜启源，邢文训，谢金星，等.大学数学实验［M］.北京:清华大学出版社，2005.JIANG Q Y，XIN W X，XIE J X ，et al．． University Mathematics Experiment［M］. Beijing:Tsinghua University Publishing House，2005.( in Chinese)