基于最优小波分组的联合信源信道编码图像传输系统
2012-10-29陈俊宏张钦宇
陈俊宏,张钦宇
(哈尔滨工业大学 深圳研究生院,广东 深圳 518055)
1 引言
随着无线通信技术的发展,多媒体通信得到日益广泛的应用,其技术的发展也越来越受重视。而作为多媒体通信技术中最重要和最基础的图像传输技术近几年来已成为一个研究热点。对于传统的基于香农分离定理的分离图像传输系统,其对编解码器的复杂性和存储能力的要求很高,在实际应用中代价太高难以满足,从而激发了对更为有效的联合信源信道编码(JSCC)方法的探索和研究。目前很多具体的基于JSCC的图像通信系统被提出[1~6]。这其中有一类重要的JSCC系统是把信源信息按照重要性程度分成不同等级,在信道编码时对不同等级实行不等错误保护(UEP)。由于在信道传输过程中,各类数据对于误比特率的敏感性是完全不同的,因此,较之UEP,对于在所有信息都采取相同程度差错控制编码的等差错保护(EEP)方法而言,在非重要信息的保护上是一种带宽的浪费,而对重要信息的保护又显得不足。因而,近年来的很多研究都集中在UEP上,像IRA码[7]、RCPC码[8]、RC-LDPC码[9]以及WICP-LDPC码[10]等大量的信道编码被应用到UEP传输系统中。
基于小波变换的图像压缩编码是一类非常优秀的图像信源编码,无论是在压缩效率上,还是在顽健性上,都有很好的性能,近几年来的大量研究使其获得了极大的成功。例如新一代的图像标准JEPG 2000的核心算法——优化截取的嵌入式编码算法(EBCOT)[11,12],其性能要优于以DCT变换为核心的上一代JEPG标准。基于SPIHT小波变换的信源编码[13],以及基于小波分组分解的图像压缩算法[14,15]等大量的基于小波变换的图像压缩编码被提出,并且均取得了很好的效果。
对基于小波分组分解的图像信源编码而言,小波分组的最优剪枝是该类算法的核心技术之一,如文献[14]中提出的在率失真意义下是最优剪枝算法。然而当图像需要经过噪声信道进行传输时,文献[14]中提出的算法由于信道噪声的影响将不再是最优剪枝算法。本文提出了一种新的基于小波分组分解的图像信源编码算法,其小波分组的剪枝算法引入了信道噪声强度和信道编码码率等参数,从而在图像有噪信道传输时仍具有全局率失真意义上的最优性。在量化编码方式上,采用可将信息按其重要性程度分成不同等级的位平面编码,从而可以很好地适用于UEP系统。将所提出的信源编码系统结合 WICP-LDPC信道编码系统,构成一个基于JSCC的图像UEP传输系统。
2 基于率失真的最优小波分组编码算法
小波分组的基本思想是通过非倍频带的分解,从而对某个给定的信号自适应地选择最好的基。对于最优基的选择,一般的方法就是定义一个代价函数,然后在这个完全树中查找一个子树,使得其全局的代价函数最小。如图1所示,在完全树的每一个分支,父亲子带的代价J(P)与其4个孩子子带的代价之和ΣJ(Ci)进行比较,如果前者更大,则这 4个子节点被保留(对应这个父节点被分解),并且将父节点的代价更新为其孩子代价之和;否则这 4个分支被剪去。当这个自底向上的树剪枝过程到达根节点时,使全局代价最小的最优子树就找到了。
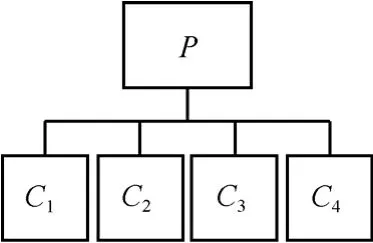
图1 完全树的一个分支
Ramchandran和 Vetterli[14]提出一个基于编码率和失真的代价函数,根据这个代价函数,小波分组分解以及每个小波分组子带的量化编码在率失真意义下是最优的,该准则通过定义以下一个Lagrange代价函数
其中,λ>0,为权重因子,用于控制编码率 R与相应失真D之间的平衡,且D是用MSE来度量。对于任意给定的一个小波分组分解,分解树的叶节点对应最终的分组子带。假设这些子带由{B1,B2,…,Bm}来表示,由于率和失真的可加性,全局代价可由式(2)表示

其中,Ri和 Di分别表示子带 Bi的总编码率和相应的总失真。
此时对小波分组的最优剪枝算法为:在完全树的每一个分支,如果式(3)满足,则父亲子带被保留;否则它被分解为4个孩子子带。当树剪枝算法到达根节点时,对于给定的 λ,可同时得到最优的小波分组分解和每个分组子带的最优量化编码方式。

以上是针对图像压缩时对小波基的选取,没有考虑到信道噪声以及信道编码的情况。在图像传输系统中,由于信道噪声的存在,需要对信源压缩后的码流进行信道编码,这样就增加了信道编码的码率,以及由信道噪声引入的失真。
假设信道编码造成的码率增加比率,既码率的倒数为σ,此时全局代价函数可写成
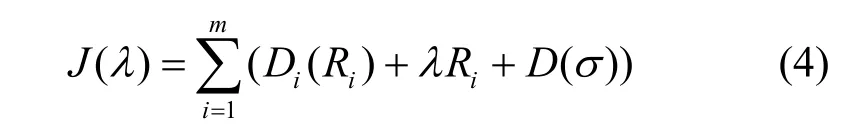
其中,D(σ)是由信道噪声引入的失真。设e为译码所得码字y与原码字x之间的误差,既e=|x-y|,则,e的期望值为
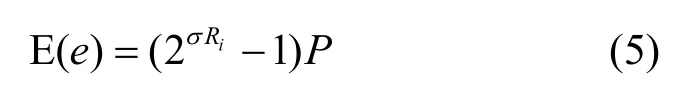
并且

其中,σRi为子带经过信道编码后的码率,1/σ即为信道编码码率;P为经过信道编码后噪声信道的误比特率,与信道噪声以及信道编码码率及编码方式相关,对于BSC信道,信道误比特率p即为式(6)中的P。而对于其他噪声信道,在给定信源信道条件下,信道编码码率与信道噪声之间具体的约束关系可由具体的编解码方法所确定的。因此可先计算出差错控制编码在各个信道信噪比和各信道编码码率下的误比特率,并存储起来,在实际的编码传输中,编码器根据当前的信道条件和传输要求,从存储表格中查找对应的信道编码码率后代入式(6)。
因而,小波分组剪枝判决式变为
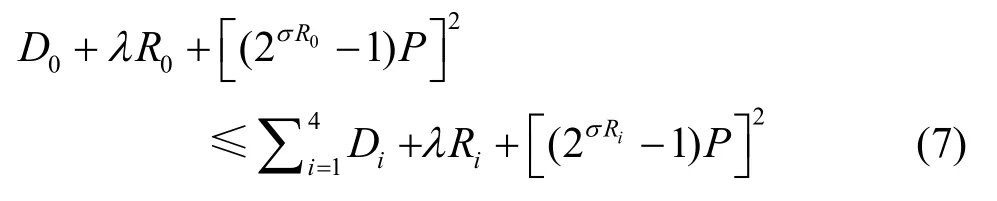
值得注意的是,从式(7)可以看出,当信道情况较好,即信噪比很大时,P的值趋于0。此时式(7)退化为式(3),得到的最优小波基即为Ramchandran和 Vetterli在文献[14]中提出的基于编码率和失真的最优小波基。
综上所述,在图像传输时,最优小波基的选择概括如下。
1) 完全分解输入图像至一个给定的分深度N,从而得到完全分解树。
2) 给定一个λ,并根据信道情况选取P值,根据信道编码的码率选择σ值,再从完全分解树的叶节点开始根据各节点的代价函数(7)进行自底向上的剪枝算法,在树的每一个节点,判断是否要保持其4个子分支。当剪枝工作完成后,就对给定的λ得到了其在噪声信道情况下最优的小波分组分解和每个分组子带的最优量化编码方式。
3) 二分法调整λ,重复上述步骤2),以满足给定的目标比特率R。
图像进行最优小波分组分解后,需要对其每个小波分组子带进行块分割编码。对于一个小波分组子带Ω,设它的一个像素点p的坐标是(i, j),该点的系数值由cij来表示。设B是子带Ω的一个子块,如果下式满足,则称块B相对于阈值n是重要的,否则称其为不重要的。
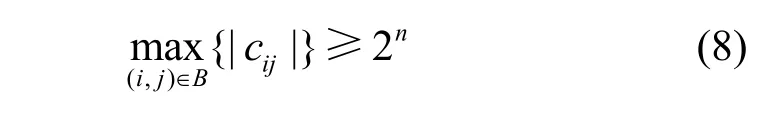
块编码算法采用位平面编码的方式,其主要目的是定位每个位平面的重要系数,同时将一组不重要系数仅用一个符号来编码。为了达到这个目标,算法总是先检测一个系数块的重要性状态。如果这个块在当前位平面n是重要的,则被分割为4个相等的子块以定位其中的重要系数,如图2所示;否则,这个块保留至下一位平面再进行重要性检测。因此可以依据位平面的重要程度对各码块进行不等差错保护信道编码。
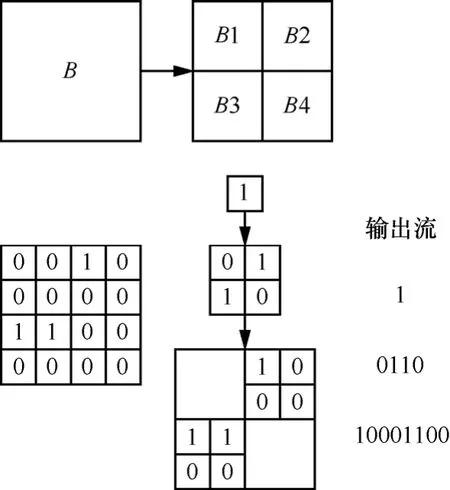
图2 对于某一阈值重要块的分割及其输出码流
3 基于WICP-LDPC码的UEP信道编码
马丕明等人在文献[10]中构建的重量递增校验矩阵的LDPC码(WICP-LDPC)具有很好的UEP性能。对于非规则LDPC编码,由于高度数的比特节点能够从邻近的校验节点得到更多的信息,因而度数高的比特节点的错误比低度的比特节点优先得到纠正,即随着比特节点度数的增加,该点的错误保护的能力变的更强。而WICP-LDPC可以成功地实现重要信息到非规则LDPC高度比特点的映射,从而达到UEP的目的。
对于第2节中的最优小波分组编码,假设其阈值的最大值为N,显然阈值为N的位平面具有最高的重要级别,随着阈值的减小后面几层的重要性依次降低。在WIPC-LDPC的信息节点选取N个不同度数,假设每个度数的信息节点数分别为S1,S2,…,SN,其中,SN这些信息节点对应的度数最大,S1这些信息节点对应的度数最小,则编码分以下2步。
1) 按图3所示,重新排列图像码流,组成新的信息矢量V。首先从阈值为N的位平面码流中由前往后取SNbit,然后从第N-1层平面由前往后取SN-1bit…,从第1层平面由前往后取S1bit按照如下的顺序组成一个信息矢量。即第1层的码流比特放在最后面,最后一层的码流比特放在最前面。循环以上的过程,当某一位平面的数据比特取完后,继续按照重要的信息比特放在信息矢量后面的原则在相邻平面取数据,直到把所有的码流比特都按照上述的结构组成信息矢量。

图3 信息矢量的构成
2) 对排列后的信息矢量 V进行系统编码。使用WICP-LDPC方法完成信息矢量V到编码码字x的编码。
4 联合编码方案
综上所述,传输系统的联合编码方案如图 4所示,对于给定的信道及总的传输速率要求,通过查表获得P值,根据信道编码的码率获得σ值,代入式(7)中,并对信源图像进行小波分组分解后的剪枝。对各小波子带系数进行位平面编码,再将高位面的编码码流映射到WICP-LDPC的高度比特点,完成联合编码过程。
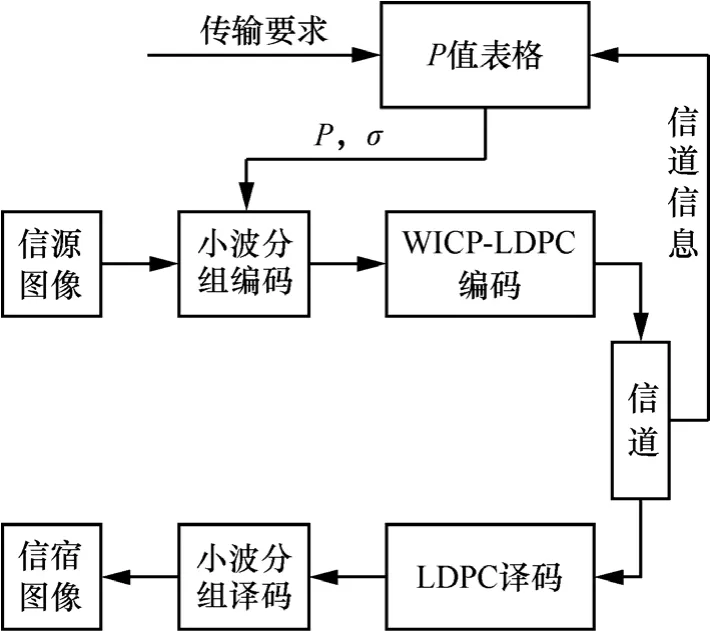
图4 信源信道联合编码图像传输系统
5 仿真实验和分析
实验采用标准8bit灰度图像Lena、Goldhill和Barbara在BSC信道上进行仿真。选取3组码率为1/2的非规则LDPC码,分别对其生成矩阵进行初等变换,将会得到3组列重递增校验矩阵的非规则LDPC码,利用这3组WIPC-LDPC码作为传输系统的信道编码进行对比实验。
选取的第1组信道编码码长为8 192,码率1/2,即(8 192, 4 096)非规则LDPC码,其生成列多项式为
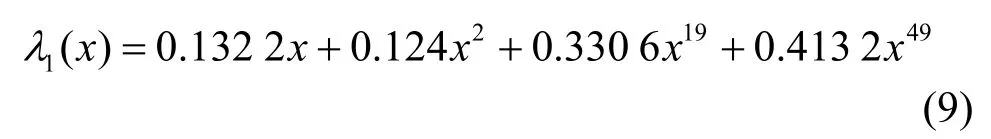
行多项式为

第2组非规则LDPC码为(10 000, 5 000),其生成列多项式为
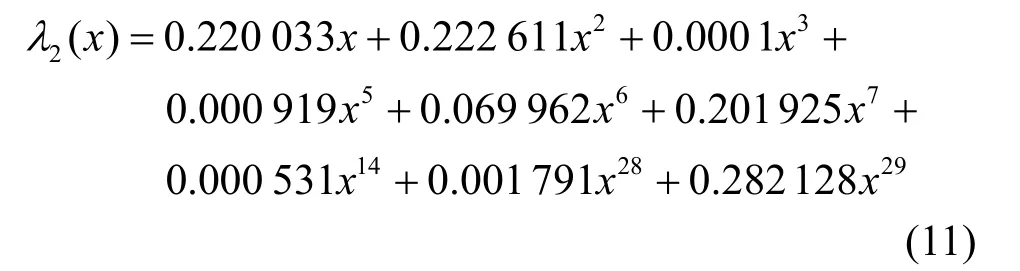
行多项式为

第3组非规则LDPC码为(10 000, 5 000),其生成列多项式为

行多项式为
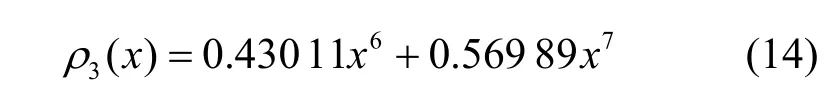
所选取的3组WIPC-LDPC码的各项参数见表1。
由于信道编码的码率为 0.5,因而在信源编码时,参数σ=2再结合BSC信道的误比特率p完成信源编码,其中小波分组分解使用了 Daubechies 9/7-tap滤波器组,分解深度为5,图5分别给出了Lena图在BER为0.01,0.05,0.1时,用式(7)作为小波分组剪枝判决式,剪枝后的小波分解框架,同时作为对比,图5中也给出了信道噪声为0时,即剪枝判决式(7)退化为式(3)时Lena图的小波分解结构。可以看到,在信噪比较大时小波分组分解框架的变动较小。

表1 各组WIPC-LDPC参数

图5 不同BER下Lena图的小波分解结构
信道编码时先按所述方法将图像码率排列成信息矢量,再进行系统编码。图6、图7分别给出了实验中 3幅图像在传输码率为 0.5bit/pixel和0.25bit/pixel时重建图像的峰值信噪比PSNR与BSC信道误比特率BER之间的关系。
由表1可以看出,第1组WIPC-LDPC码的最高级别比特节点的度数最大,与其他级别节点间性能差异最明显,但其最优比特的数量却最少,只占有效比特的 12.5%,而第 2组和第 3组却占到了16.3%和29.7%,因而可以认为其UEP的特征更明显。从图 6和图 7中可以看出采用第 1组的WIPC-LDPC编码的重构图像效果要好于第2组和第3组的。为了更进一步地对比,用式(9)和式(10)生成的 LDPC码,即第 1组 WIPC-LDPC的生成LDPC码作为信道编码,做了EEP传输模式下的仿真实验,其结果如图6和图7所示。显然,UEP方案要优于EEP,并且这种优势在信道条件恶劣的情况下更加明显。此外,在使用WIPC-LDPC作为信道编码的UEP传输时,WIPC-LDPC码的UEP特征越明显,其传输效果越好。
由于篇幅所限,在这里仅给出了Lena在信道BER为0.03和0.1时,不同传输码率下的重建图像,如图 8所示,其中,图 8(a)和图 8(b)传输码率为0.25bit/pixel,图8(c)和图8(d)传输码率为0.5bit/pixel。
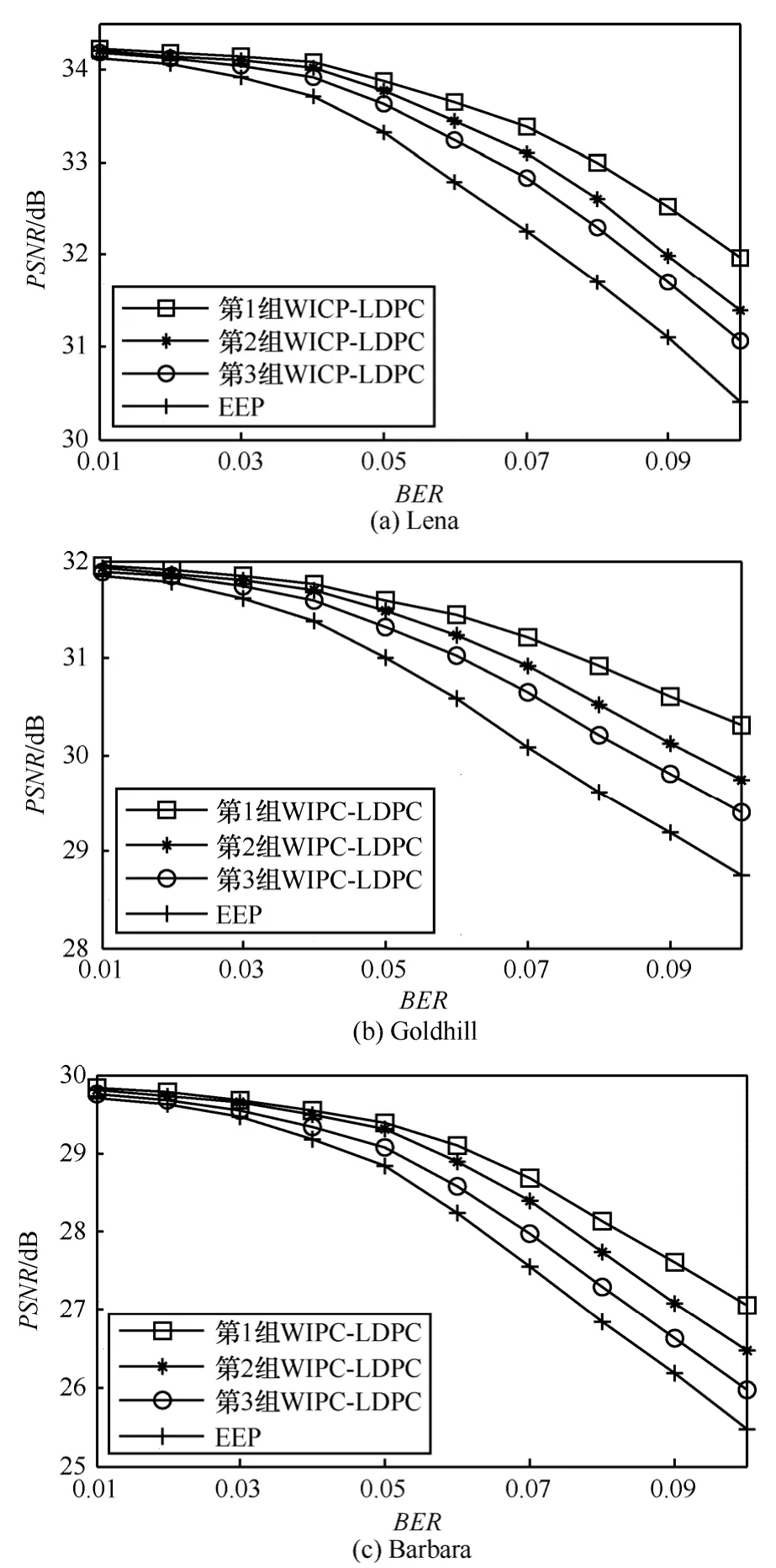
图6 传输码率为0.5bit/pixel时重建图像的PSNR
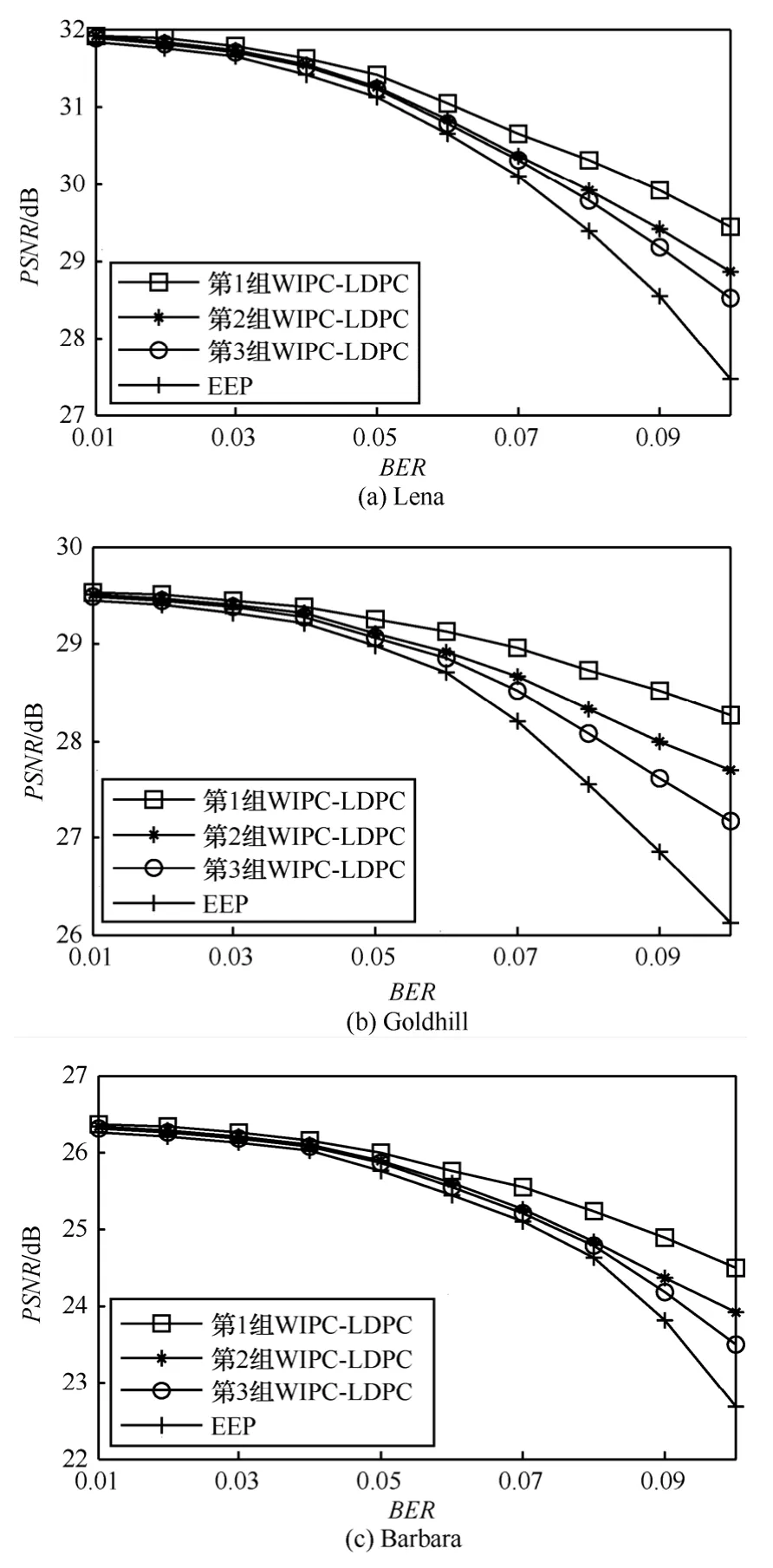
图7 传输码率为0.25bit/pixel时重建图像的PSNR

图8 Lena的重建图像
表2和表3给出了几种近几年提出的图像传输系统与本文所提出系统的比较,其中,Fresia等人在文献[4]中提出的系统使用 JPEG 2000和RC-Turbo码作为传输系统的信源信道编码器,Lan等人在文献[7]中的系统使用了 SPIHT和 IRA,Sanchez在文献[8]中提出的系统则使用了 JPEG 2000和RCPC码。在传输码率为0.25bit/pixel时,三幅重建图像的PSNR值如表2所示,表3为传输码率在0.5bit/pixel时,3幅重建图像的PSNR值。
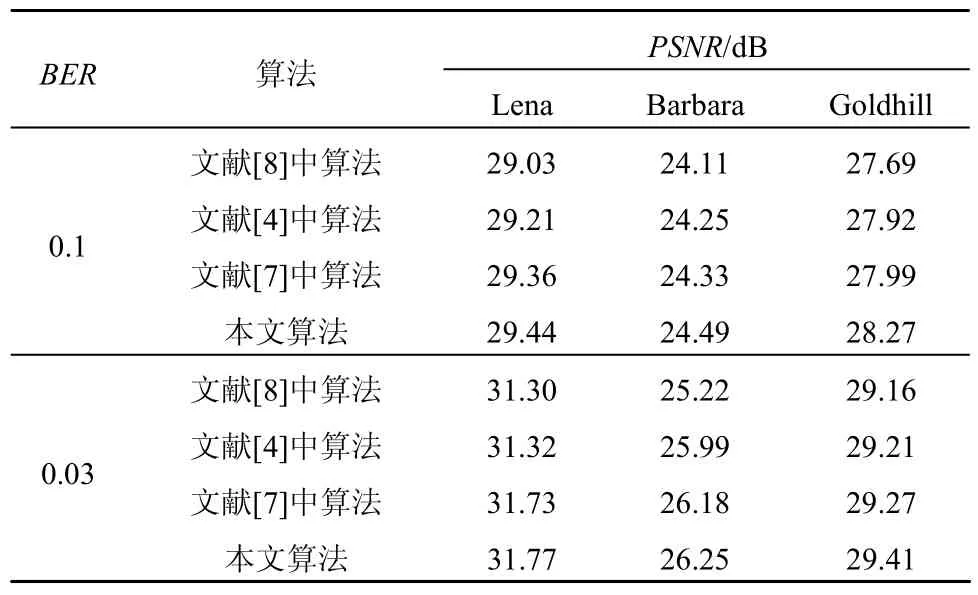
表2 传输码率为0.25bit/pixel时,重建图像的PSNR值
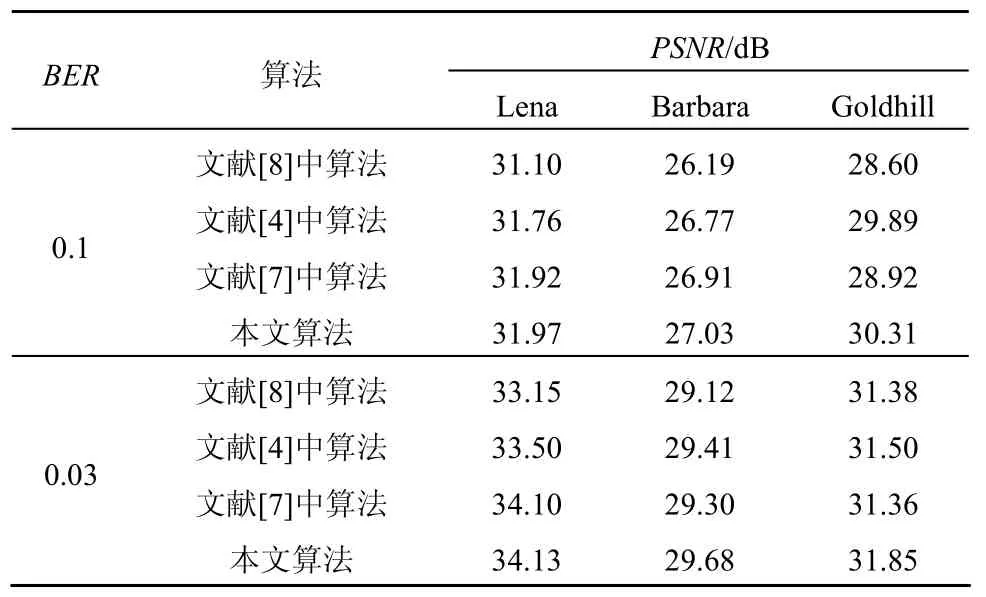
表3 传输码率为0.5bit/pixel时,重建图像的PSNR值
文献[7]所提出的传输系统使用SPIHT作为信源编码,信道编码使用IRA码,其中,IRA码是一种具有接近香农限性能的码,与本文所使用的信道编码类似,其UEP特性主要也体现在不同度数的节点具有不同的抗误码能力上,该系统在传输Lena图时具有很好的性能,本文所提出方法与其相比只有微弱的优势(平均0.05dB的增益),特别是在高信噪比的传输条件下(只有0.03dB的增益),这是由于在信噪比较高的情况下Lena图像的最优小波分组分解结构基本上就是通常的金字塔分解,因而在最优小波分解结构与金字塔分解差异较大的 Barbara和Goldhill图的实验中具有更高增益,Barbara平均提高0.19dB,Goldhill平均提高0.58dB。文献[4]和文献[8]所提出的系统均使用JPEG 2000作为信源编码器,在信道编码时,也均采用了率兼容的信道编码对信源图像进行分级保护,其中文献[4]中使用的RC-Turbo码的性能更优,然而这2种信道编码与本文所使用的WIPC-LDPC码及IRA码相较而言,不具备线性时间编码和译码的特性。对于Lena图,本文所提出方法比文献[4]所使用的方法平均提高0.33dB,对于Barbara和Goldhill图,其平均PSNR的提高分别是0.26dB和0.33dB。图9给出了Lena图在传输总码率为0.25bit/pixel,信道BER为0.03时重建图像的放大细节,从中可以看出本文所提出的方法比文献[4,7,8]中的方法保持了更多的细节信息。
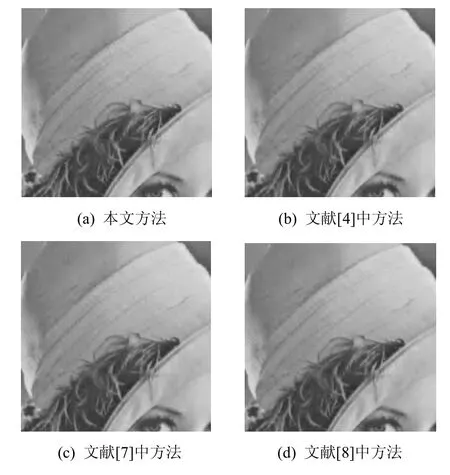
图9 Lena在传输码率为0.25bit/pixel信道,BER为0.03时重建图像的放大细节
与使用固定子带分解的图像传输方法相比,本文所提出的方法在信源编码时的计算复杂度相对较大,这主要是因为算法需要对完全分解树进行多次剪枝以及查找最优小波分组分解,但是这一部分计算均在发送端完成,而在接收端的信道译码所耗费时间却要低于文献[4, 7, 8]中使用的方法。
6 结束语
本文提出了一种在率失真意义上具有最优的基于小波分组分解的图像编码算法。所提出的图像编码器在信源编码过程中引入了信道误比特率P以及信道编码的码率σ等参数,将信道信息及信道编码情况考虑到信源编码中来,采用联合信源信道编码的方式来实现图像在有噪信道中的可靠传输。构建了以WIPC-LDPC码作为信道编码的图像传输系统,从BSC信道的仿真结果上来看,所提出的方法具有很好的性能,无论从主观质量上,还是在客观度量上,均要优于Fresia、Lan和Sanchez等人提出的方法。在进一步的工作中,将对查找最优小波分组分解的快速算法进行研究。
[1] SHERWOOD P G, ZEGER K. Progressive image coding for noisy channels[J]. IEEE Signal Processing Letter, 1997, 4(7): 189-191.
[2] BABUSTER B, BELZER B, FISCHER T. Robust image transmission using JPEG 2000 and turbo-codes[J]. IEEE Signal Processing Letter,2002, 9(4): 117-119.
[3] PAN X, BANIHASHEMI A H, CUHADAR A. A fast trellis-based rate-allocation algorithm for robust transmission of progressively coded images over noisy channels[J]. Transactions on Communications, 2006, 54(1): 1-6.
[4] FRESIA M, LAVAGETTO F. Determination of optimal distortion-based protection in progressive image transmission: a heuristic approach[J].Transactions on Image Processing, 2008, 17(9): 1654-1662.
[5] KIM H, ANNAVAJJALA R, COSMAN P, et al. Source-channel rate optimization for progressive image transmission over block fading relay channels[J]. IEEE Transactions on Communications, 2010, 58(6):1631-1642.
[6] SABIR M F, BOVIK A, HEATH R, et al. Unequal power allocation for JPEG transmission over MIMO systems[J]. IEEE Transactions on Image Processing, 2010, 19(2): 410-421.
[7] LAN C, XIONG Z, NARAYANAN K R. Source-optimized irregular repeat accumulate codes with inherent unequal error protection capabilities and their application to scalable image transmission[J]. Transactions on Image Processing, 2006, 15(7): 1740-1750.
[8] SANCHEZ V, MANDAL M K. Efficient channel protection for JPEG2000 bitstream[J]. IEEE Transactions on Circuits Syst Video Technology, 2004, 14(4): 554-558.
[9] PAN X, CUHADAR A, BANIHASHEMI A H. Combined source and channel coding with JPEG 2000 and rate-compatible low-density parity-check codes[J]. IEEE Transactions on Signal Processing, 2006,54(3): 1160-1164.
[10] 马丕明, 袁东风, 杨秀梅. 非规则LDPC码的不等错误保护性能研究[J]. 通信学报, 2005, 26(11): 132-136.MA P M, YUAN D F, YANG X M. Research on unequal error protection of irregular LDPC codes[J]. Journal on Communications, 2005,26(11): 132-136.
[11] ATZORI L. Transmission of JPEG 2000 images over wireless channels with unequal power distribution[J]. IEEE Trans Consumer Electronics, 2003, 49(4): 883-888.
[12] MAHIN T, ATOUSA H. Unequal power allocation for transmission of JPEG2000 images over wireless channels[A]. 2009 IEEE Global Telecommunications Conference (GLOBECOM'09)[C]. Honolulu,2009. 3279-3284.
[13] 肖嵩, 张方, 吴成柯. 基于小波 SPIHT的联合信源信道编码新方法[J]. 计算机学报, 2003, 26(3): 281-286.XIAO S, ZHANG F, WU K C. A new method of joint channel coding based on SPIHT[J]. Chinese Journal of Computers, 2003, 26(3): 281-286.
[14] RAMCHANDRAN K, VETTERLI M. Best wavelet packet bases in a rate-distortion sense[J]. IEEE Trans Image Process, 1993, 2(4): 160-175.
[15] YANG Y, XU C. A wavelet packet-based rate-distortion optimization algorithm for block partitioning image coding[J]. Sci China Ser F: Information Sciences, 2008, 51(8): 1036-1054.
