基于峰值流量的网络行为特征及影响因子分析

周爱平，程光

(东南大学 计算机科学与工程学院，教育部计算机网络和信息集成重点实验室，江苏 南京 211189）

1 引言

互联网流量的特征一直是网络测量的研究热点之一。大量研究表明网络流量具有长相关性、自相似性和突发性[1～3]。IP业务由于突发性对网络带宽的需求变得越来越大，从而网络流量突发性的研究在网络带宽需求估计中显得尤其重要。网络带宽需求的估计是网络容量规划的依据和基础。网络容量规划的目标是网络容量足够满足网络流量的突发性。文中提出的峰值流量表示在繁忙时间内的最大吞吐量，一定程度上反映了网络流量的突发性[4,5]。Van De Meent R[6]等提出了基于拇指规则的网络容量规则，规则如下：

其中，C表示目标网络容量，M表示网络带宽需求，d（ 1d≥ ）是一个常数，表示足够的网络容量满足带宽需求M的突发性。

目前，通过在不同的聚合等级上建立整个流量过程模型来解决容量规划的问题已经取得了一些成果。在报文级上，经典的排队论利用马尔科夫到达和服务时间为容量规划提供了一个架构。然而，依据互联网流量的自相似性，这样的假设不再适用[7]。在流级上，Berger A等[8]提出了基于流测度的容量规划模型，该模型对流特征的变化非常敏感，在实际应用中几乎是不可行的，而峰值流量测度更具有顽健性和实用性。Giordano S等[9]提出了一种基于聚合测度和流测度的混合模型，聚合测度与网络负载有关，流测度与流的特征相关。Van De Meent R等[6]对混合模型进行改进，利用聚合流量的方差对流量突发性建模。上述的2种方法，假定在整个分析过程中平均流量需求是恒定的，作者主要考虑网络流量突发性。根据网络流量平稳性假设，这些方法只适用于短期的网络容量规划，而不适用于长期的网络容量规划。Paxson V等[10]研究结果表明网络流量平稳性假设与遵循人类行为的流量模式相违背。在应用级上，Marques-Neto H T等[11]把每个用户流量需求描述为一种典型应用会话的综合，如Web浏览，P2P，即时通信和email，而该模型需要正确地鉴别每个应用，对用户请求模式的改变非常敏感，不适用于流量预测。Papagiannaki K等[12]通过建立整个流量测量图模型解决容量规划问题，还给出了在大时间尺度上的流量测量值，首先对流量测量值进行聚合，然后利用小波变换和方差分析对聚合数据进行压缩处理。

本文提出的方法能够有效克服上述文献中的局限性。首先提出了峰值流量的相关概念，研究峰值流量的特征,发现峰值流量服从高斯分布，及其具有相互独立性。其次分别建立方差分析模型和协方差分析模型研究网络的内在特征（主要指接入带宽和网络用户数）对峰值流量的影响，发现接入带宽对峰值流量的影响较小，而网络用户数对峰值流量的影响较大。然后建立基于网络用户数的线性回归模型，实验结果表明网络用户数与峰值流量的均值和标准差之间存在线性关系，最后利用峰值流量的高斯性及网络用户数与峰值流量的均值或标准差之间的线性关系，在式（1）基础上建立基于网络用户数的容量规划模型，通过新建校园网对该模型进行了有效性验证，实验结果表明在缺乏网络流量测量值的情况下，能够准确评估新建校园网的接入带宽。峰值流量测度既简化了数据采集、存储、管理和分析的过程，又能够有效地进行链路容量规划，更具有实用性和顽健性。

2 相关概念

定义 1 平均吞吐量(HT(t))指一条链路或路径在内能够传输数据量的平均值。

式中，A(t)表示链路在单位时间内能够传输的数据量。

定义 2 峰值流量(X)指平均吞吐量(HT(t))在内取得的最大值。

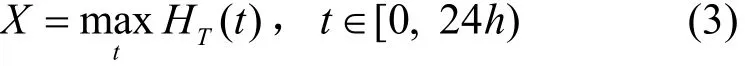
定义 4 离差系数(CV)指吞吐量标准差与峰值流量的比值。

式(5)中，Xi, Vi, CVi分别表示第i天的峰值流量、吞吐量方差及离差系数，离差系数反映了峰值流量与它的均值之间的偏离程度。

3 测量数据集

本文所使用的实验数据来源于江苏省教育和科研网边界到国家主干路由之间采集的Netflow数据[13]，抽样比率为1∶2 048, 时间粒度为5min，数据采集时间从2011年3月1日到5月31日。对Netflow数据进一步处理得到近似吞吐量A(t)，根据吞吐量A(t)计算每天的峰值流量X和吞吐量方差V，得到时间序列{Xi, i=1,2,…,N}和{Vi, i=1,2,…,N}。图1显示了持续3天的吞吐量(A(t))，峰值流量({ Xi, i =1,2,3 })和吞吐量方差({ Vi, i = 1,2,3 })。

图1 U1的连续3天吞吐量，峰值流量及吞吐量方差

为了能够有效地进行容量规划，剔除时间序列中的节假日的峰值流量。网络升级和配置改变也可能对峰值流量的特征产生不利影响，排除在 2011年已经升级或配置改变的大学网络。经过上述处理得到的数据集包含来自 13个大学网络的样本，此数据集具有了所谓的网络内在特征，如接入带宽、网络用户数等。表1给出了每个大学网络的接入带宽、网络用户数、最大峰值流量及带宽最大利用率。从表1可知，所有链路利用率比较低，即使在高负载的情况下，也低于30%，平均链路利用率大约为25%,在最重负载下，U2的链路最大利用率也低于60%。链路的低利用率使得覆盖效应失效，主要原因是最大峰值流量远远没有达到链路的最大接入带宽，而在具有高链路利用率的低接入带宽下，覆盖效应将会产生显著效果。

4 峰值流量的行为特征分析

4.1 峰值流量的高斯分布

利用式（6）和式（7）计算峰值流量的均值和标准差的估计值，如表2的第2、3列所示。

其次，给出了最大离差系数

最大离差系数表明了网络流量的突发性行为，如表2的第4列所示。

最后，根据零假设，峰值流量服从均值为μˆUj，方差为σ ˆU2j的高斯分布。通过Q-Q图判断零假设是否成立。如果峰值流量的散点图组成的直线越接近对角线，表示峰值流量分布越接近高斯分布。如图2所示，U1的大部分峰值流量值分布在对角线的周围，所以接受零假设，表明大学网络的峰值流量进行Q-Q图检验，得到类似的结果。

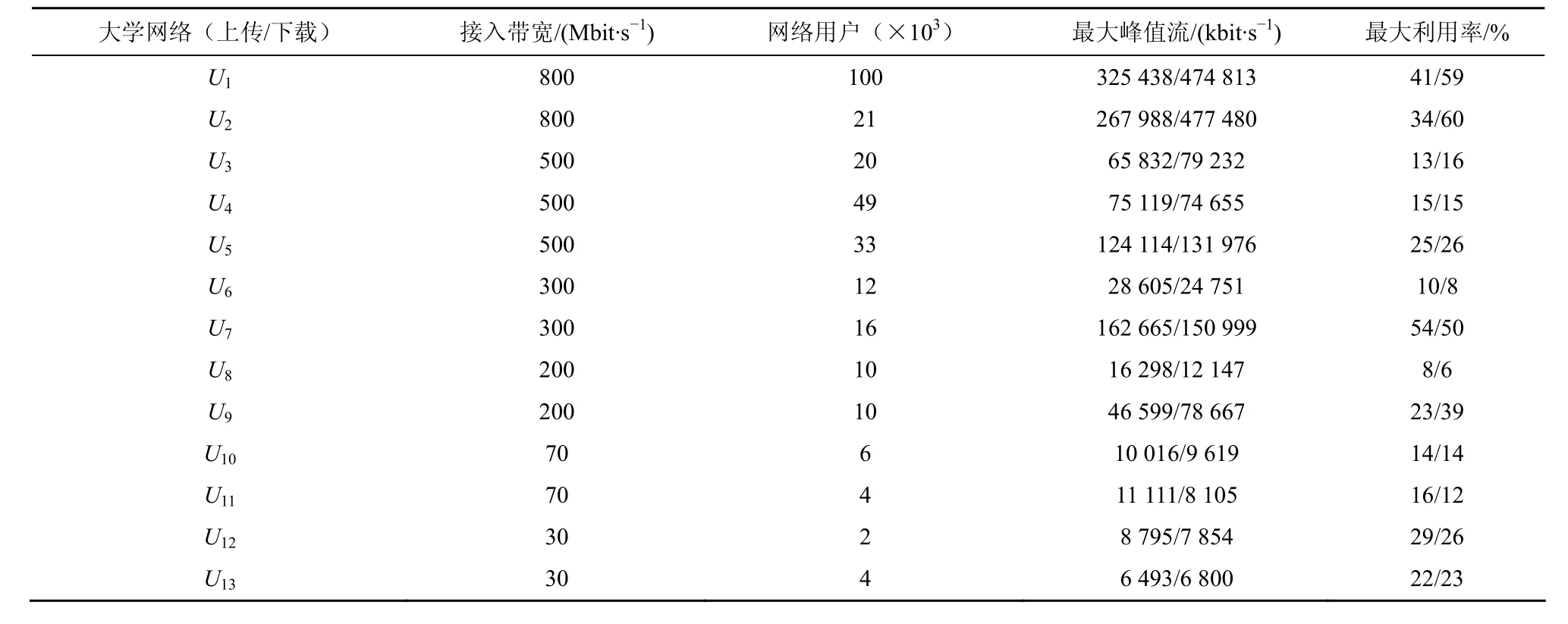
表1 大学网络的内在特征，最大峰值流量及最大利用率

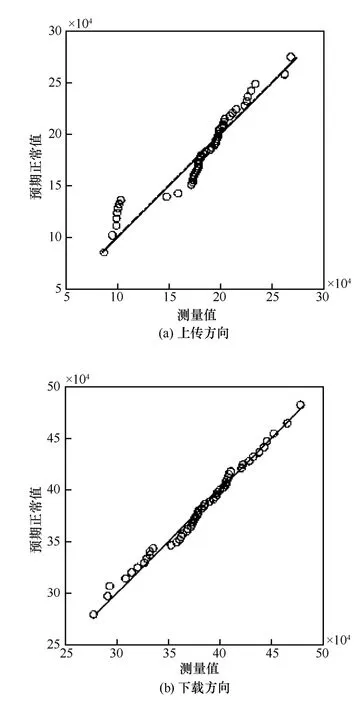
图2 U1的峰值流量的正态分布

另外，利用拟合优度检验对峰值流量的高斯分布进行客观评价。表 2最后一列给出了 Shapiro-Wilk[14]拟合优度检验的结果，绝大部分大学网络通过了拟合优度检验，从而进一步说明大学网络的峰值流量服从高斯分布。斜体部分表示没有通过拟合优度检验，拟合优度检验失效可能是网络流量的异常值造成的。综合上述分析，表明大学网络的峰值流量分布渐近高斯分布。

4.2 峰值流量的自相关实验

自相关函数反映了同一序列在不同时刻的取值之间的相关程度。通过自相关实验研究连续的峰值流量之间是否存在相关性。图3显示了其中2个大学网络在上传和下载方向上的自相关系数和置信水平为95%的置信区间。由图3可知，大学网络U1和 U2的绝大部分自相关系数落在置信区间内，从而验证了连续的峰值流量之间不存在相关性，其余大学网络均有类似的结果。

5 峰值流量的影响因子分析

前面的实验结果表明，峰值流量服从高斯分布N(μ, σ2)，参数 μ 和 σ2可以通过峰值流量的均值和方差进行估计。下面的实验研究网络的内在特征（包括接入带宽、网络用户数、大学的类型及大学教职工与学生的比率等）是否对参数μ和σ产生影响以及影响的大小[15,16]，本文运用统计学方法，如方差分析，协方差分析[17]，主要研究接入带宽和网络用户数对参数μ和σ的影响。

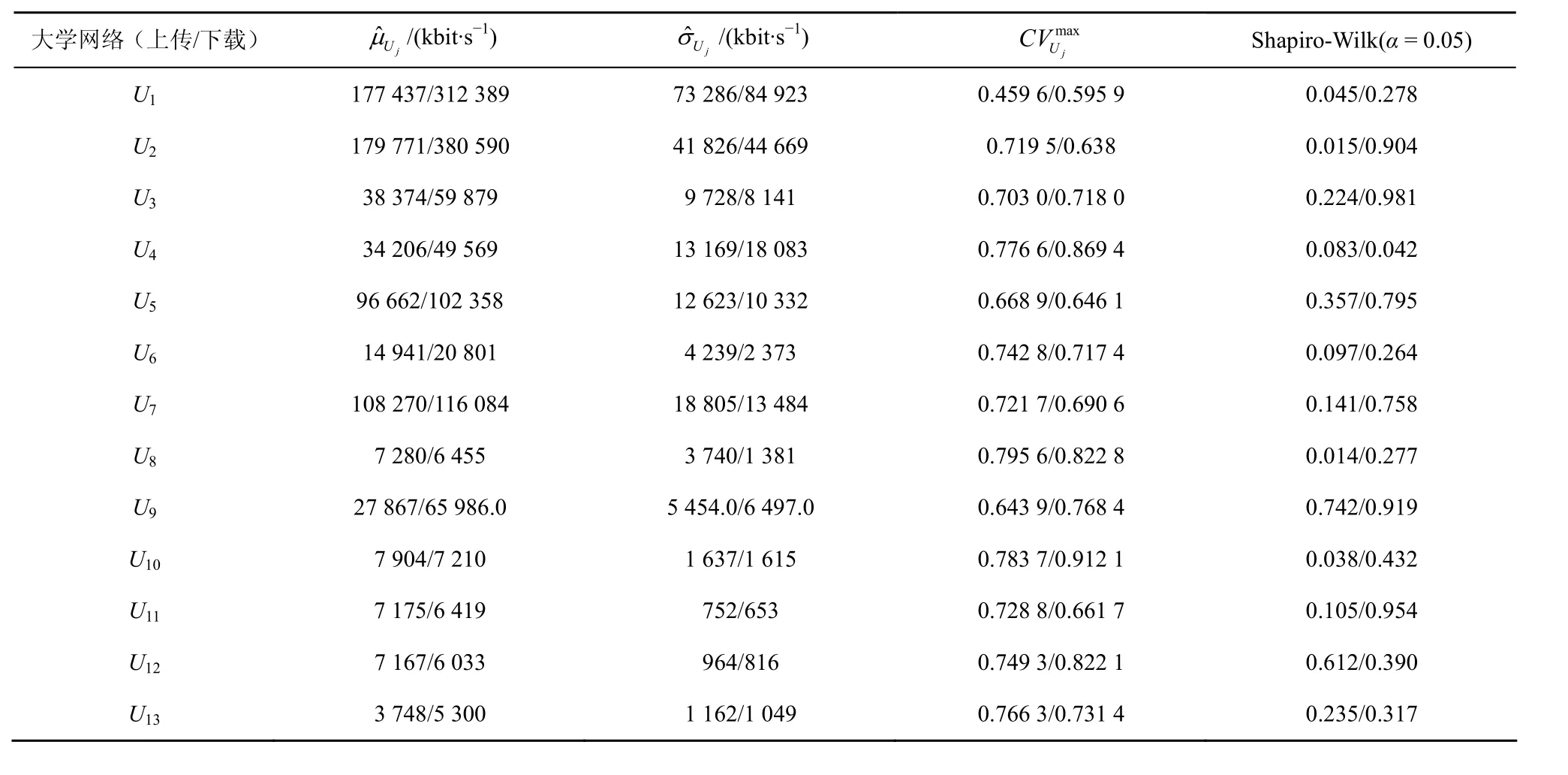
表2 峰值流量的均值、标准差、最大偏差系数及拟合优度检验结果

方差分析和协方差分析需要满足以下3个前提条件：①样本服从正态分布；②样本方差均相等；③样本之间是独立的。如果每组的元素的个数是相似的，并且没有严重偏离同方差性假设，则方差分析和协方差分析的结果一般是可以接受的。另外，协方差分析模型假设自变量与因变量之间存在相关性。

根据表1中接入带宽的大小对大学网络进行分组，接入带宽在 300Mbit/s以上的大学网络归为一组，其余大学网络归为另一组。

图3 U1和U2的自相关系数及95%的置信区间

5.1 基于接入带宽的方差分析

对于每个大学网络 Uj，接入带宽 BUj和网络用户数 PUi均是已知的，第4部分的实验只是考虑接入带宽 BUj，而没有考虑网络用户数 PUj。下面的实验仅仅研究接入带宽对峰值流量的影响，将接入带宽 BUj作为控制变量，把参数μUj和σUj作为观测变量。

方差分析是检验多组样本均值间的差异是否具有统计意义的一种统计方法。方差分析过程如下：

1) 将观测变量μUj(或σUj)分成2组，并提出零假设；

2) 计算组间离差平方和与组内离差平方和；

3) 选择F值检验，F统计量的观测值等于平均组间平方和与平均组内平方和之比，计算F统计量的观测值和概率p值；

4) 给出显著性水平 α(α = 0.05)。如果 p ＞ α，接受零假设，表明样本来自相同的正态总体，组间没有显著差异；如果p ＜ α，拒绝零假设，表明样本来自不同的正态总体，分组的均值差异有统计意义。通过方差分析可以知道不同变量的变异对总变异的贡献大小，确定控制变量对观测变量的影响大小。对接入带宽BUj为控制变量和参数μUj（或σUj）为观测变量，建立方差分析模型

其中，ky是观测变量y的总体均值，为了和观测变

表3显示了峰值流量的均值μ和标准差σ的方差分析结果。由表3可知，p值均大于显著性水平α（α = 0.05），表明接入带宽因子对均值和标准差均没有显著影响，组内的离差平方和占总的离差平方和的百分比较高，分别为91%，84%，82%，86%，进一步表明接入带宽对峰值流量的影响较小，可能还有其他因子影响峰值流量。

5.2 基于接入带宽和网络用户数的协方差分析

协方差分析是一种结合回归分析与方差分析的统计方法。在协方差分析中，先将定量的影响因素看作自变量，或称为协变量，建立因变量随自变量变化的回归方程，这样就可以利用回归方程把因变量的变化中受不易控制的定量因素（协变量）的影响去除掉，再将定性的影响因素看作自变量，建立因变量随自变量变化的方差分析模型。把网络用户数看作定量变量（或协变量），接入带宽看作定量变量，峰值流量的均值或方差看作因变量。对式(9)进行扩展建立协方差分析模型表示网络用户数对峰值流量的影响。

表3 接入带宽为自变量，参数μ和σ为因变量的方差分析结果

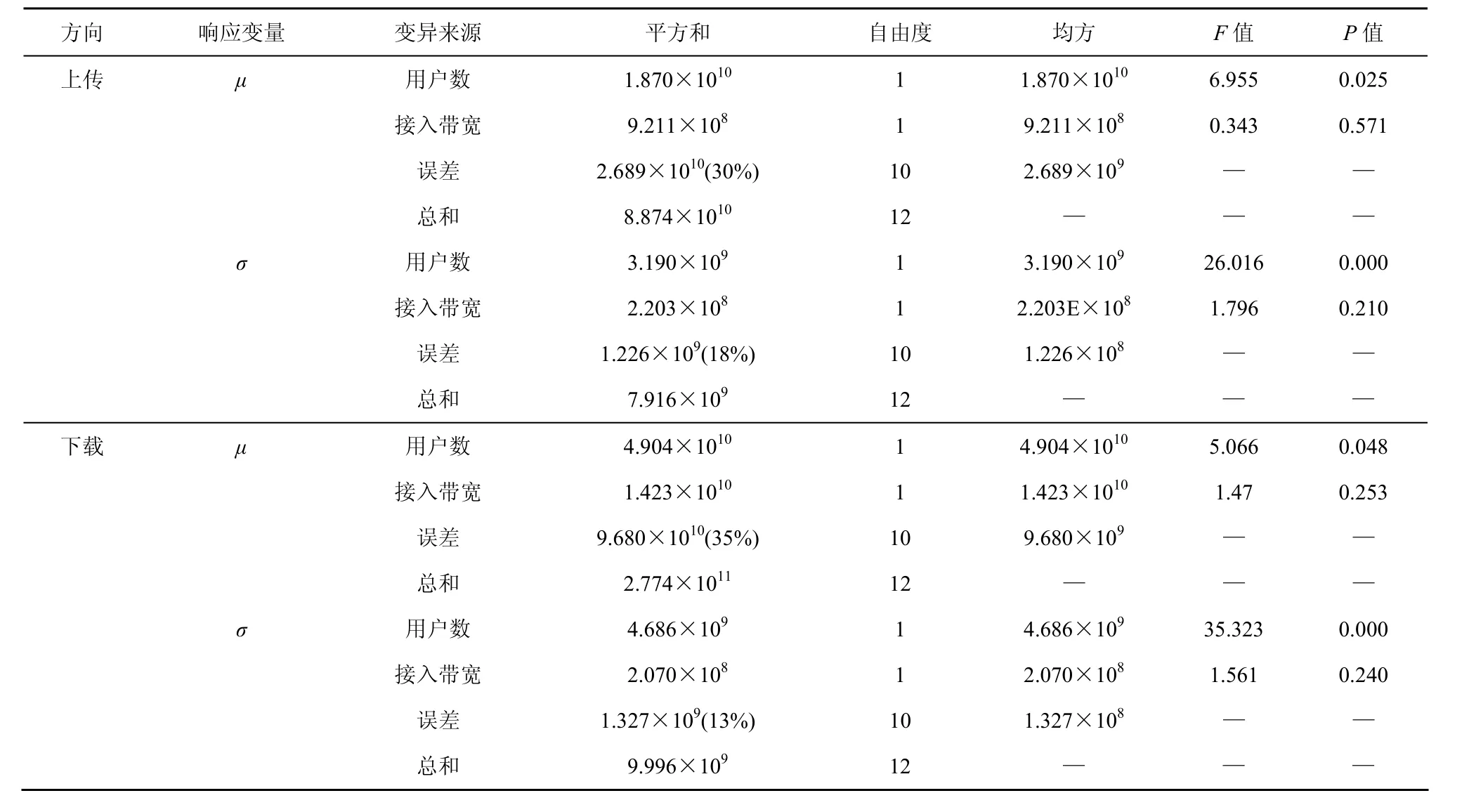
表4 接入带宽为自变量，网络用户数为协变量，参数μ和σ为因变量的协方差分析结果

协方差分析先利用回归分析消除网络用户数对峰值流量的影响，再利用方差分析分析接入带宽对峰值流量的影响。表4给出了协方差分析的结果。由表4可知，协变量网络用户数的离差平方和对总的离差平方和的贡献明显增加，表明组内的离差平方和所占总离差平方和的比例显著减少。相比于方差分析的结果，对于峰值流量的均值 μ，组内的离差平方和在上传和下载方向上分别减少到 30%和35%，对于峰值流量的标准差 σ，组内的离差平方和在上传和下载方向上分别减少到18%和13%，而方差分析模型将接入带宽作为惟一的影响因子，对于峰值流量的均值 μ，组内的离差平方和在上传和下载方向上分别高达91%和82%，对于峰值流量的标准差 σ，组内的离差平方和在上传和下载方向上分别高达84%和86%。

由上述分析可知，接入带宽贡献的离差平方和大小是由于接入带宽与网络用户数的相关性造成的，而不仅仅是接入带宽的影响，从而表明接入带宽不是影响峰值流量的主要因素。

5.3 基于网络用户数的线性回归分析

由上述可知，协方差分析利用线性回归消除协变量对总的离差平方和的影响，从而将网络用户数作为自变量，建立线性回归模型准确评价网络用户数对峰值流量的影响。为了简化模型，对于所有的大学网络，假设βgroup是相同的，用β表示βgroup，建立线性回归的简化模型

该模型只把网络用户数 PUj作为影响峰值流量的分布N (μ, σ2)的唯一因子。β表示线性回归模型的斜率，即每个网络用户对峰值流量的均值μUj贡献的流量大小。当考虑基于网络用户数的链路容量规划时，β是一个关键的参数。

表5给出了模型的回归系数和95%的置信区间。对于大学网络 Uj，网络用户数 PUj，在下载方向上接入带宽需求 CUj= 2 6431 + 2 772⋅PUj，其中，2 772表示每个网络用户对接入带宽贡献的大小。利用峰值流量的高斯性及网络用户数与峰值流量的均值或方差之间的线性关系，在式（1）的基础上建立了一个基于网络用户数的链路容量规划模型

式中， ε ～ N ( 0,σε2) ，且 ε ≤ 0.1。

在缺少网络流量测量值的情况下，该方法能够准确评估新建校园网的带宽需求，还可以用来估计网络用户数随着时间变化的校园网的带宽需求。

表5 参数μ、σ的线性回归系数及95%的置信区间

5.4 验证模型

这部分实验主要验证容量规划模型对新建校园网的有效性。表6给出了8个新建校园网的内在特征，以及参数μ和σ的估计值。图4给出了模型数据，回归直线，验证数据以及参数μ和σ的95%的置信区间。由图4可知，绝大部分验证数据落在模型的95%的置信区间内，说明了容量规划模型的有效性，其中有极少部分大学网络的流量测量值落在置信区间外，表明在相同网络用户数的情况下其产生更多的网络流量，而模型数据中也有极少部分大学网络的流量测量值落在置信区间外，表明其与上述的大学具有类似的行为，造成这种现象的原因可能是工科类大学每个网络用户对网络流量的需求比其他类型大学更高，以及不同学生与教职工的比率也会造成不同大学的网络流量需求差异。从而表明该模型未能充分考虑不同类型大学及不同学生与教职工的比率的大学网络用户的流量需求差异。考虑更多的影响因素（如大学类型、学生与教职工的比率），权衡模型评估的准确性和时间复杂度，建立优化的容量规划模型进一步解释这种现象，也是今后研究的一个方向。

表6 大学网络的内在特征，峰值流量的均值及标准差

图4 线性回归模型的验证结果

6 结束语

本文对21个CERNET校园网的峰值流量进行深入研究，研究表明峰值流量服从高斯分布，不同天的峰值流量之间相互独立，因此，在几个月内网络流量可以利用峰值流量的高斯分布均值和方差进行估计。通过建立方差分析模型和协方差分析模型，研究网络的内在特征对峰值流量的影响，方差分析结果表明在链路的最大利用率远远未达到接入带宽的情况下，接入带宽对峰值流量的影响较小，协方差分析结果表明网络用户数是影响峰值流量的主要因素。最后建立基于网络用户数的线性回归模型，实验结果表明网络用户数与峰值流量均值和标准差之间存在线性关系。由此利用峰值流量的高斯性及网络用户数与峰值流量的均值或标准差之间的线性关系，建立一个基于网络用户数的网络容量规划模型，同时验证了该模型对新建校园网链路容量规划的有效性，在缺乏网络流量测量值的情况下，准确评估新建校园网的接入带宽。峰值流量既简化了数据采集、存储、管理和分析的过程，又能够有效地进行容量规划，更具有实用性和顽健性。虽然网络用户数对总的离差平方和贡献较大，使得组内的离差平方和的比例显著减小，还需考虑更多的内在特征建立优化模型，获得更准确的估计值。分析网络的其他内在特征（比如大学的类型、大学的学生与教职工的比率等）对峰值流量的影响以及建立优化的容量规划模型将作为下一步的研究目标。

[1] GONG W, LIU Y, MISRA V, et al. Self-similarity and long range dependence on the internet: second look at the evidence origins and implications[J]. Computer Networks, 2005, 48(3): 377-399.

[2] BERAN J, SHERMAN R, TAQQU M S, et al. Long-range dependence in variable-bit-rate video traffic[J]. IEEE Transactions on Communications, 1995, 43(234): 1566-1579.

[3] YIN Q H, JIANG Y M, JIANG S M, et al. Analysis on generalized stochastically bounded bursty traffic for communication networks[A].Proceedings of IEEE Conference on Local Computer Networks(LCN’02)[C]. Tampa, Florida, USA, 2002. 141-149.

[4] GARCÍA-DORADO J L, HERNÁNDEZ J A, ARACIL J, et al. Characterization of the busy-hour traffic of IP networks based on their intrinsic features[J]. Computers Networks, 2011, 55(9): 2111-2125.

[5] ZINK M, SUH K, GU Y, et al. Characteristics of Youtube network traffic at a campus network-measurements, models, and implications[J].Computer Networks, 2009, 53(4): 501-514.

[6] MEENT R V D, MANDJES M R H, PRAS A. Smart dimensioning of IP network links[A]. Proceedings of IFIP/IEEE International Workshop on Distributed Systems: Operations and Management[C]. San José, USA, 2007. 86-97.

[7] CROVELLA M E, BESTAVROS A. Self-similarity in World Wide Web traffic: evidence and possible causes[J]. IEEE/ACM Transactions on Networking, 1997, 5(6): 835-846.

[8] BERGER A, KOGAN Y. Dimensioning bandwidth for elastic traffic in high-speed data networks[J]. IEEE/ACM Transactions on Networking,2000, 8(5): 643-654.

[9] GIORDANO S, SALSANO S, Van den Berghe S, et al. Advanced QoS provisioning in IP networks: the european premium IP projects[J].IEEE Communications Magazine, 2003, 41 (1): 30-36.

[10] PAXSON V, FLOYD S. Why we don’t know how to simulate the Internet[A]. Proceedings of the 29th Conference on Winter Simulation[C]. Washington, USA, 1997. 1037-1044.

[11] MARQUES-NETO H T, ALMEIDA J M, ROCHA L C D, et al. A characterization of broadband user behavior and their e-business activities[J]. SIGMETRICS Performance Evaluation Review, 2004,32(3): 3-13.

[12] PAPAGIANNAKI K, TAFT N, ZHANG Z L, et al. Long-term forecasting of Internet backbone traffic: observations and initial models[A]. Proceedings of IEEE INFOCOM[C]. Burlingame, CA, USA,2003.1178-1188.

[13] ESTAN C, KEYS K, MOORE D, et al. Building a better netflow[A].Proceedings of ACM SIGCOMM[C]. New York, USA. 2004.245-256.

[14] LESLIE J R, STEPHENS M A, FOTOPOULOS S. Asymptotic distribution of the Shapiro-Wilk W for testing for normality[J]. The Annals of Statistics, 1986, 14(4): 1497-1506.

[15] GARCÍA-DORADO J L, HERNÁNDEZ J A, ARACIL J, et al. On the duration and spatial characteristics of Internet traffic measurement experiments[J]. IEEE Communications Magazine, 2008, 46(11): 148-155.

[16] WANG J H, AN C Q, YANG J H. A study of traffic, user behavior and pricing policies in a large campus network[J]. Computer Communications, 2011, 34(16): 1922-1931.

[17] KESELMAN H J, HUBERTY C J, LIX L M, et al. Statistical practices of educational researchers: an analysis of their ANOVA, MANOVA,and ANCOVA analysis[J]. Review of Education Research, 1998, 68(3):350-386.