基于信念传播的分布式最大权匹配算法

张源

（东南大学 移动通信国家重点实验室，江苏 南京 210096）

1 引言

考虑一个一般的无向图G=(V, E)，其中V代表所有节点的集合，E代表所有边的集合。考虑E的某个子集，如果其中任意2条边都没有交点，则称该子集为图G的一个匹配（match）。假设每条边e∈E都被赋予一个正权重 we，则本文研究最大权匹配（MWM）问题，即寻找具有最大权重和的匹配。在形式上，MWM问题可以描述为下列二值线性整数规划问题：

其中，xe=1或0分别代表边e是或不是匹配的边，N(i)是所有与节点i相连的边构成的集合。

最大权匹配问题是一个非常基本的数学问题[1]，并且能被用于解决大量实际问题。在无线网络领域中，有各种无线资源分配与调度问题，其核心就是寻找给定图的最大权匹配如文献[2,3]。因此，高效的MWM算法，对于解决无线网络中的资源调配问题是非常重要的。事实上，在图论、组合优化等数学领域中针对该问题的研究已经相当充分与完整，并已提出了大量算法[4,5]。然而，这些算法都是中心式的，即需要有某个中心节点知道整个图的全局信息。在无线网络中，一般来说是不存在这种能掌握全局信息的中心节点的，而必须采用能够分布式执行的最大权匹配算法。因此，这些算法是无法直接应用于无线网络中。

在文献[6,7]中，已经提出了几种分布式MWM算法。这些算法都是基于贪婪（greedy）原则，非常简单，其找出的匹配质量一般较低（本文第4节中的仿真结果也说明了这一点）。近年来，又出现了一类全新的基于信念传播（belief propagation）的方法。该方法来自人工智能与机器学习领域，并且已被成功应用于信道编码问题[8]。文献[9,10]将该方法应用于MWM问题，并提出了一类基于信念传播的分布式MWM算法。该算法内容如下：首先，该算法以迭代方式运行。在每次迭代过程中，每条边f=(k,i)向邻边e=(i,j)发送消息mf→e，其计算公式为

其中，符号(x)+代表取x与0中的大者。根据所有接收到的消息，每条边e计算度量。

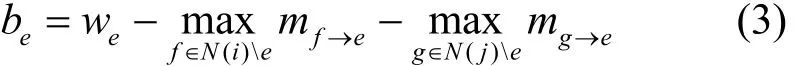
根据该度量，每条边e进行如下判断

其中，问号代表不确定情形。下文将称该算法为MWM问题的BP算法。文献[9,10]已证明该算法当图G为二分图（bipartite）时等价于拍卖（auction）算法[11]，并且当MWM唯一时保证收敛至最优解。然而，当图G是一般含圈图时，则只证明了当式(1)的松弛线性规划没有分数解时才能收敛至最优解。值得一提的是，针对最大权独立子集（MWIS）问题的类似算法在文献[12]中也得到了研究。

2 BP算法

本文主要分析BP算法的不足，揭示其产生的原因，然后针对这些不足对原有BP算法进行改进。本节提及的各命题及证明统一在第3节中给出。事实上，BP算法主要存在两方面的不足。首先，BP算法非常容易出现振荡现象，从而导致不收敛。为此，引入了信念传播圈的概念，并且在引理1中给予证明，式(2)更新消息时，如果图中存在信念传播圈，那么该圈中相邻边间的消息有可能在二值间振荡取值。这就是BP算法中的振荡现象。第4节中的仿真结果也展现了这一点。为了消除振荡，建议修改式(2)中的消息计算公式为

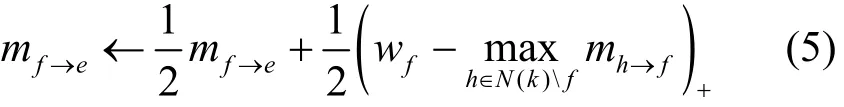
从而得到一个改进的BP算法。进一步地，在定理1中证明了，如果根据式(5)更新消息，则可以消除振荡问题。

除了振荡现象，BP算法还可能出现所谓不确定现象。该现象的起因是，当边e根据式(4)进行判决时，如果be=0，应该如何处理？如果判决xe=1，则最终解可能不正确，即出现匹配边相邻的情形；如果判决为xe=0，则最终解可能不是最优的。这就是BP算法中的不确定现象。文献[9,10]中并没有研究这一问题。本文首先在引理4中证明，如果be＞0，所有与e相邻的边f都有bf＜0，不会出现bf=0的情形。接下来，在引理5中证明，如果be=0，则所有与e相邻的边f都有bf≤0，并且边e每侧有且仅有一条边的度量为0，即不确定。综合这2条引理，可以说明，在图中所有的不确定边一定构成一个圈。在定义3中称这样的圈为不确定圈。在引理7中证明，在不确定圈上执行信念传播算法，仍然得到不确定圈。因此，BP算法是不适用于不确定圈的，必须采用新方法处理不确定情形。根据引理8，建议采用下列简单的方法。如果边e发现自己是不确定的，即be=0，则边e要沿着不确定圈发送探针（probe），分别将所有奇数边与偶数边的权重和保存在不同的变量中，即

然后返回边e，其中，边1为边e，边2为边e顺时针一侧的邻边，依次类推。假设不确定圈包括n条边。如果n=2k，则根据下式进行判决

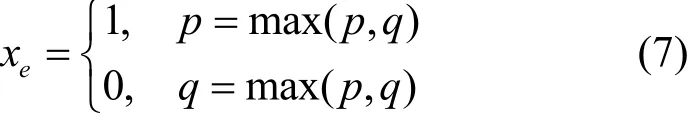
如果n=2k+1，则需要进一步计算

其中，w2k+1是边e逆时针一侧的邻边的权重，然后根据下式进行判决

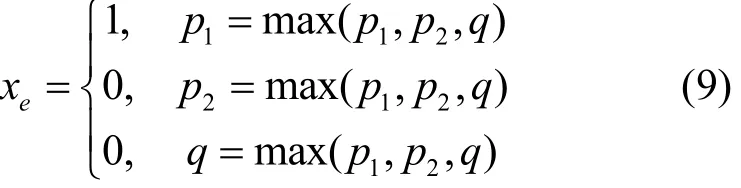
综上，BP算法主要在振荡与不确定2个方面存在不足。针对这些不足，改进BP算法将主要包括如下2个阶段。在第1阶段，相邻边之间根据式(5)交换消息直至收敛。在第2阶段，每条边根据式(3)计算度量，如果 be＞0则判决 xe=1，如果be＜0则判决xe=0，如果be=0，则根据式(7)或式(9)进行判决。最后，在定理2中证明了该改进算法是正确的。计算机仿真实验结果表明，该改进算法可以显著提高信念传播类算法在一般图中寻找最大权匹配的能力，具体内容将在第4节中给出。

3 算法分析

定义1 考虑任意边f=(k,i)，如果

则称h*为f在节点k侧的下游边。

定义2 考虑图1中所示的一组边1，2，…，n，n+1，并且边k+1是边k的下游边（1≤k≤n），如果n+1=1，则称这n条边构成一个信念传播圈；如果n+1=Ø，则边n一定位于图的边缘，并称这n条边构成一条信念传播路径。

图1 信念传播圈与路径

引理1 给定信念传播圈包括n条边，如果n为奇数，则其中任意相邻边间消息的取值有可能不收敛，并且是在2个数值之间振荡取值。

证明 考虑信念传播圈中的任意一条消息m1→n。根据定义2，则该消息的计算公式为

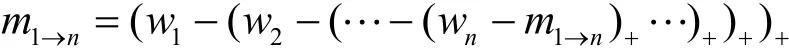
定义函数

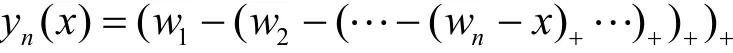
可以通过归纳法证明，当n为奇数时，函数yn(x)的形状必为图2(a)～图2(d)、图2(e)和图2(j)中之一；当n为偶数时，函数yn(x)的形状必为图2(f)～图2(i)、图2(e)和图2(j)中之一。

证明如下：当 n=1时，y1(x)=(w1-x)+，其形状为图 2(a)中所示；当 n=2时，y2(x)=(w1-(w2-x)+)+=(w1-y1(x))+，当 w1＞w2时，其形状为图 2(g)中所示；当w1=w2时，其形状为图2(f)中所示；当w1＜w2时，其形状为图2(h)中所示。假设n=k时命题成立。当n=k+1时，yk+1(x)=(w1-yk(x))+。如果k为奇数，如果yk(x)的形状为图2(a)中所示，依据w1与yk(x)大小关系的不同，yk+1(x)的形状为图2(f)～图2(h)中所示之一；如果yk(x)的形状为图2(b)中所示，则yk+1(x)的形状为图2(e)～图2(h)中所示之一；如果yk(x)的形状为图2(c)中所示，则yk+1(x)的形状为图2(e)～图2(h)和图2(i)中所示之一；如果yk(x)的形状为图2(d)中所示，则yk+1(x)的形状为图2(e)～图2(h)和图2(i)中所示之一；如果yk(x)的形状为图2(e)中所示，则yk+1(x)的形状为图2(j)中所示；如果yk(x)的形状为图2(j)中所示，则yk+1(x)的形状为图2(e)和图2(j)中所示之一。如果k为偶数，推导过程是类似的。从而命题得证。

消息 m1→n的取值就是方程 x=yn(x)的解。具体来说，就是根据xt+1=yn(xt)的迭代方程确定m1→n取值，其中上标代表迭代次数。分3种情形分析如下。

1) 当n为偶数时，yn(x)的形状为图2(e)～图2(j)中之一，该迭代过程一定收敛。

2) 当n为奇数时，如果yn(x)的形状为图2(e)和图2(j)中之一，或者yn(x)的形状为图2(a)～图2(d)中之一，即其中包含有一段斜率为负 1的斜线段，但方程 x=yn(x)的解不在该斜线段上，则该迭代过程一定收敛。

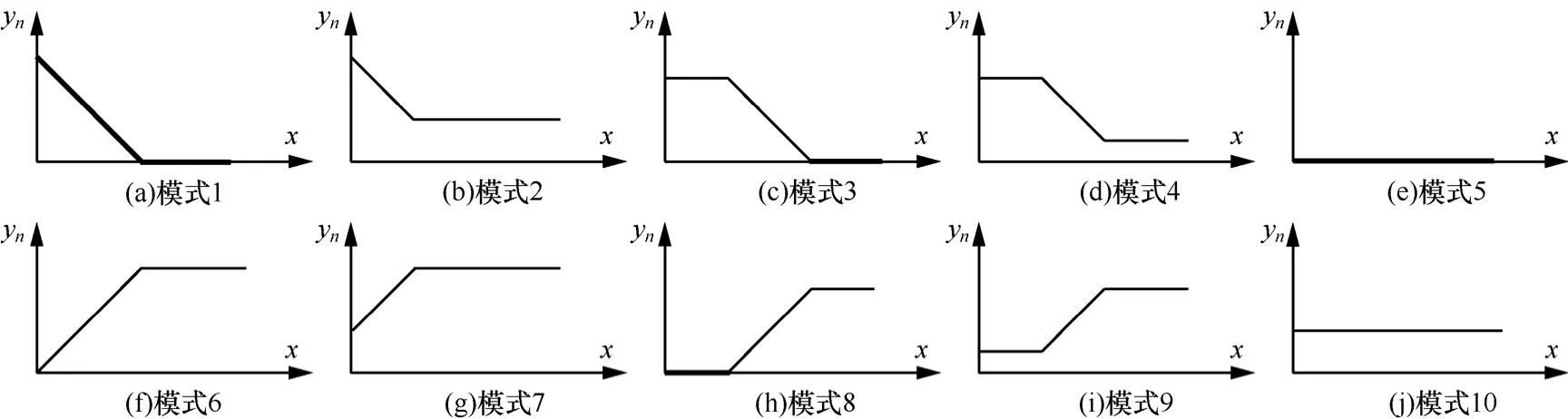
图2 消息计算模式

3) 当n为奇数时，如果yn(x)的形状为图2(a)～图2(d)中之一，且方程x=yn(x)的解就落在其中的斜线段上，则可以证明该迭代过程不收敛，且 m1→n在2个数值之间振荡取值。记斜线段的自变量范围为a≤x≤b，方程x=yn(x)的解为x*。假设迭代从某x0（a≤x0＜x*≤b）开始，则 x1=yn(x0)=2x*-x0，x2=yn(x1)=x0等。这样，m1→n将在 x0与 x1之间振荡取值。类似地，如果迭代从某x0（a≤x*＜x0≤b）开始，m1→n也将在2个数值之间振荡取值。

综上，当n为奇数时，信念传播圈中消息计算过程可能不收敛。如果不收敛，则消息将在2个数之间振荡取值。证毕。

引理 2 给定信念传播路径，其中任意相邻边间消息的取值一定收敛。

证明 假设信念传播路径包括n条边，考虑其中任意一条消息 me→e-1。根据定义 2，该消息的计算公式为

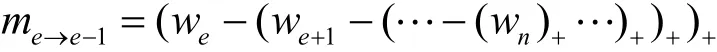
该计算过程是确定的，因此一定是收敛的。所以，信念传播路径中相邻边间消息计算的过程都是收敛的。证毕。

定理1 如果根据式(5)计算消息，给定信念传播圈，其中任意相邻边间消息的取值一定是收敛的。

证明 假设信念传播圈包括n条边，并考虑其中消息 m1→n。根据式(5)更新消息，其取值将通过明，分3种情形，分析如下。

1) 当n为偶数时，yn(x)的形状为图2(e)～图2(j)

2) 当n为奇数时，如果yn(x)的形状为图2(e)～图 2(j)中之一，或者 yn(x)的形状为图 2(a)～图 2(d)中之一，且方程x=yn(x)的解不在斜线段上，则类似可知迭代过程收敛。

3) 当n为奇数时，如果yn(x)的形状为图2(a)～图2(d)中之一，且方程x=yn(x)的解就落在其中斜线段上，

引理 3 考虑与边 f=(k,i)一侧相邻的任意 2条边 e=(i,j)与 h=(i,l)，则 mf→e=mf→h。

证明 根据消息的定义可得。证毕。

引理4 如果边e的度量be＞0，则所有与e相邻的边f都有 bf＜0。

证明 根据条件，be=we-mf*→e-mg*→e＞0，其中f*与 g*是分别从两端与 e相邻且消息取值最大的边，如图 3所示。考虑边 e的任一相邻边 f，则bf=wf-mh*→f-me*→f，其中，h*与 e*是分别与 f相邻且消息取值最大的边。根据消息计算公式we-mg*→e=me→f， 有 be=me→f-mf*→e＞0 ， 即 me→f＞mf*→e。再根据 e*的含义，则有 me*→f≥me→f＞mf*→e。另一方面，考虑 bf，根据消息计算公式wf-mh*→f=mf→e，有 bf=mf→e-me*→f。将 me*→f＞mf*→e代入，则有 bf＜mf→e-mf*→e，再根据 f*的含义，则有mf→e≤mf*→e，从而得到 bf＜0。证毕。

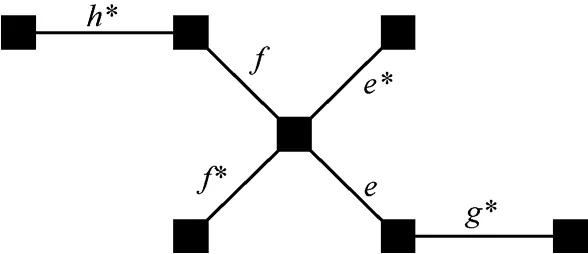
图3 引理4的证明

引理5 如果边e的度量be=0，则所有与e相邻的边f都有bf≤0；进一步地，如果假设每条边的下游边是唯一的，则边e每侧有且仅有一条边的度量为0。

证明 如图 4所示，be=we-mf*→e-mg*→e=0，其中f*与g*是分别从两端与e相邻且消息取值最大的边。由于 we-mg*→e=me→f，则 be=me→f*-mf*→e=0，即me→f=mf*→e。考虑边 e的任一相邻边 f，则bf=wf-mh*→f-me*→f，其中，h*与 e*是分别与 f相邻且消息取值最大的边。由于wf-mh*→f=mf→e，再考虑到 e*与 f*的含义，则有 bf=mf→e-me*→f≤mf*→e-me*→f= me→f-me*→f≤0。接下来考虑该引理中的第2部分，以边e的i节点一侧为例。考虑边f*，其度量为bf*=wf*-mh*→f*-me*→f*，其中，h*与 e*是分别与 f*相邻且消息取值最大的边。由于wf*-mh*→f*=mf*→e，则有bf*=mf*→e-me*→f*。可以证明 e*=e。根据 f*的含义可知 mf*→e≥me*→e，根据 be=0 可知 me→f*=mf*→e，因此有 me→f*=mf*→e≥me*→e=me*→f*。再根据 e*的含义可知 me*→f*≥me→f*，从而有 me*→f*=me→f*。由于假设边f*的下游边是唯一的，则有e*=e。这样，可以得到bf*=mf*→e-me→f*=0，并且是唯一的。证毕。

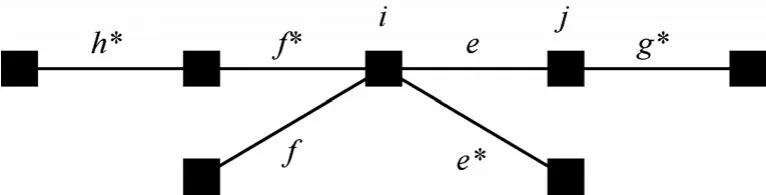
图4 引理5的证明

定义 3 由所有度量为零的边构成的圈为不确定圈。

引理6 不确定圈一定是信念传播圈。

证明 在不确定圈上，根据引理5的证明，其中任意2条相邻边都互为下游边，从而符合信念传播圈的定义。证毕。

引理 7 在不确定圈上执行信念传播算法，仍然得到不确定圈。

证明 在不确定圈上，根据引理5的证明，其中任意2条相邻边都互为下游边。因此，不论是在原图中还是单独在不确定圈上，所执行的性能传播算法是完全相同的，从而仍然得到不确定圈。证毕。

引理8 假设不确定圈包括n条边，记为1，2，…，n。如果n为偶数，即n=2k，则最大权匹配的权和为max(w1+w3+…+w2k-1, w2+w4+…+w2k)；如果n为奇数，即 n=2k+1，则最大权匹配的权和为 max(w1+w3+…+w2k-1, w3+w5+…+w2k+1, w2+w4+…+w2k)。

证明 在不确定圈中，可能的匹配方案就是依次选择边。具体分析如下。如果n是偶数，则有2种选择，即 x2i=1（1≤i≤k），相应的权和为 w1+w3+…+w2k-1；或者 x2i-1=1（1≤i≤k），相应的权和为w2+w4+…+w2k。因此，最大权匹配的权和为max(w1+w3+…+w2k-1, w2+w4+…+w2k)。如果n是奇数，则有3种选择，即x1=x3=…=x2k-1=1，相应的权和为 w1+w3+…+w2k-1；或者 x2=x4=…=x2k=1，相应的权和为 w2+w4+…+w2k；或者 x3=x5=…=x2k+1=1，相应的权和为w3+w5+…+w2k+1。因此，最大权匹配的权和为 max(w1+w3+…+w2k-1, w3+w5+…+w2k+1,w2+w4+…+w2k)。证毕。

定理 2 在改进算法执行过程中，所有得到的解都是满足匹配要求的。

证明 需要证明的是，迭代算法的每次输出一定满足匹配要求，即所有被选中的边都是不相邻的。在改进算法中，一条边被选中有2种可能。1）该边不是不确定的。在这种情况下，根据引理4可知，所有与该边相邻的边的度量都将严格的小于零，是一定不会被选中的，从而保证了正确性。2）该边是不确定的。在这种情况下，根据引理5可知，所有与该边相邻的边的度量或者严格小于零，或者也是不确定的。考虑与该边相邻的不确定边。由于改进算法中采用式(7)或式(9)处理不确定情形，并能达到引理8中给出的权和性能，位于同一不确定圈上的不确定边一定是交替成为匹配边的，因此被选中的边一定都是不相邻的，从而保证了正确性。证毕。

4 仿真

首先考虑比较小型的含圈图，有4个节点，并且任意2个节点间都有边相连，即一个4阶完全图（complete graph）。图中每条边都随机产生一个0～1之间的正实数作为权重，然后分别运行BP算法与改进的BP算法，并记录下每2条相邻边之间发送消息的迭代计算过程。图 5中给出了一次典型的运行结果，从实验结果可以看出，BP算法采用式(2)计算消息，消息的取值出现了明显的振荡现象，而改进的BP算法由于采用式(5)计算消息，其消息的计算过程是收敛的，从而解决了这一问题。进一步地，统计了每种仿真场景下所有 1 000次仿真的收敛情况，BP算法与改进的BP算法都有可能出现不收敛，其中BP算法有286次不收敛，而改进的BP算法只有42次不收敛，明显优于BP算法。综合该组仿真结果可以知道，改进BP算法算法虽然未能完全解决一般图情形下不收敛的问题，但与BP算法相比已经有了非常明显的改善。因此，该组仿真结果表明，改进BP算法的收敛性能明显优于BP算法。

接下来研究改进算法的性能。仿真场景如下。假设在 1km×1km的正方形区域内随机分布若干节点，其中，如果任意2个节点之间距离小于某一门限值，则令这2个节点间有边相连，并且每条边都随机产生一个0～1之间的正实数作为权重，这样就可以得到一个随机的加权图。在仿真中假设门限值为0.4km。针对给定图，将分别运行3种不同的分布式MWM算法。第1种算法是文献[6]中的基于贪婪的分布式MWM算法；第2种算法是文献[9,10]中的BP算法；第3种算法就是本文提出的改进BP算法。另外，还将通过求解优化模型(1)来计算给定图中的最大权匹配，作为分布式算法性能的上限。值得说明的是，对传统BP算法来说，由于传统BP算法由于振荡与不确定问题，很可能不收敛，最终输出结果很可能是不匹配的，从而导致经常得到超过最优解的性能。因此本文是搜集了所有BP算法输出正确匹配的结果（如图6所示）。

在仿真中分别假设节点总数在10～30间取值。在不同的节点总数下，随机生成100组不同的节点分布并得到相应的图，对每张图分别运行前述 2种分布式MWM算法及最优化方法，然后把100次仿真的结果平均起来作为该节点总数下的仿真结果。从图6中可以看出，本文所提出的改进算法的性能与最优化方法几乎是相同的，与传统的BP算法或贪婪算法相比性能改进是显著的。这组仿真结果充分说明本文所提出的改进BP算法在性能上的优越性。

图5 消息的迭代计算过程

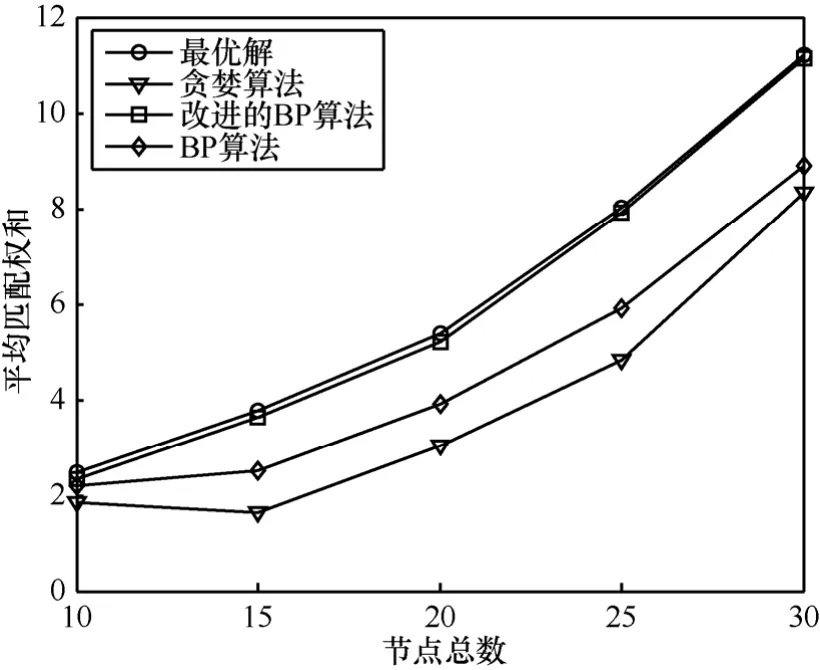
图6 分布式匹配算法性能比较

5 结束语

本文研究了一般图的最大权匹配的分布式算法。以基于信念传播的分布式算法为基础，分析了原有算法的振荡问题并提出一种改进的相邻节点间交换消息的方法，分析了原有算法中的不确定问题，并提出了一种新的处理方法以保证算法的正确性，从而得到一种新的改进算法。仿真结果表明，与已有算法相比，改进算法可以收敛至与最优解非常接近的程度，这种算法具有更好的收敛与权重和性能。

[1] DASGUPTA S, PAPADIMITRIOU C, VAZIRANI U. Algorithms[M].New York, McGraw Hill, 2008.

[2] TASSIULAS L, SARKAR S. Maximin fair scheduling in wireless ad hoc networks[J]. IEEE Journal on Selected Areas in Communications,2005, 23(1): 163-173.

[3] CHEN L, LOW S H, CHIANG M, et al. Cross-layer congestion control, routing and scheduling design in ad hoc wireless networks[A].IEEE INFOCOM 2006[C]. Barcelona, Spain, 2006.1-13.

[4] COOK W J, CUNNINGHAM W E, PULLEYBLANK W R, et al. Combinatorial Optimization[M]. New Jersey: Dover Publications, 1998.

[5] SCHRIJVER A. Combinatorial Optimization-Polyhedra and Efficiency[M]. Berlin: Springer, 2004.

[6] HOEPMAN J. Simple distribute weighted matchings[EB/OL].http://arxiv.org /abs/cs/0410047, 2004.

[7] HOEPMAN J, KUTTEN S, LOTKER Z. Efficient distributed weighted matchings on trees[A]. Structural Information and Communication Complexity[C]. Berlin, Springer, 2006.

[8] KSCHISCHANG F R, FREY B J, LOELOGER E A. Factor graph and the sum-product algorithm[J]. IEEE Transactions on Information Theory, 2001, 47(2): 498-519.

[9] BAYATI M, SHAH D, SHARMA M. Max-product for maximum weight matching: convergence, correctness, and LP duality[J]. IEEE Transactions on Information Theory, 2008, 54(3): 1241-1251.

[10] SANGHAVI S, MALIOUTOV D, WILLSKY A S. Belief propagation and LP relaxation for weighted matching in general graphs[J]. IEEE Transactions on Information Theory, 2011, 57(4): 2203-2212.

[11] BERTSEKAS D P. Auction algorithm for network flow problems: a tutorial introduction[J]. Computational Optimization and Applications,1992, 1(1): 7-66.

[12] SANGHAVI S, SHAH D, WILLSKY A S. Message passing for maximum weight independent set[J]. IEEE Transactions on Information Theory, 2009, 55(11): 4822-4834.