基于边界加扰动的Helmhotz方程柯西问题的正则化

刘利平

基于边界加扰动的Helmhotz方程柯西问题的正则化

刘利平

（甘肃政法学院计算机科学学院，甘肃，兰州 730070）

Helmhotz方程的柯西问题是一类典型的反问题而且是不适定的，也就是说其解不连续依赖于柯西数据，即小的扰动都会导致解的爆破。文章给出了边界加扰动的正则化方法，恢复了解对数据的连续依赖性，并给出了收敛性估计。最后用数值例子说明我们的方法是有效可行的。

Helmhotz方程；柯西问题；不适定问题；边界加扰动的正则化方法；误差估计

Helmhotz型方程最初来源于物理中声、波的传播和散射，建筑物的振动以及电磁场等等[1-3]。它是一种典型的不适定问题[4]，即问题的解如果存在，将不连续依赖于定解数据[5-6]。给数值计算带来了极大的困难[7]。由于这一问题在理论和实际中有着重要的价值，人们对它的正问题（Dirichlet，Neumann 或者混合边值问题）在上世纪已经做过广泛的研究，许多数值方法被用来求解Helmhotz 方程[8-10]。

对方程(1.1)我们利用Fourier变换可以求得变换后的问题在频域中的解为：

利用Fourier逆变换可以得到该问题的精确解为:

下面来看频域中的解。

1 问题的边界加扰动正则化方法

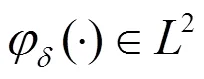
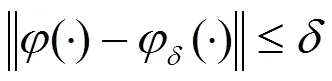
基于这一思想，我们用边界加扰动的方法来修改原问题得

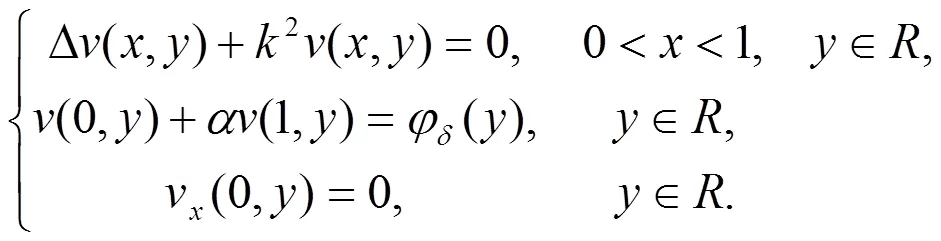
利用Fourier 变换得

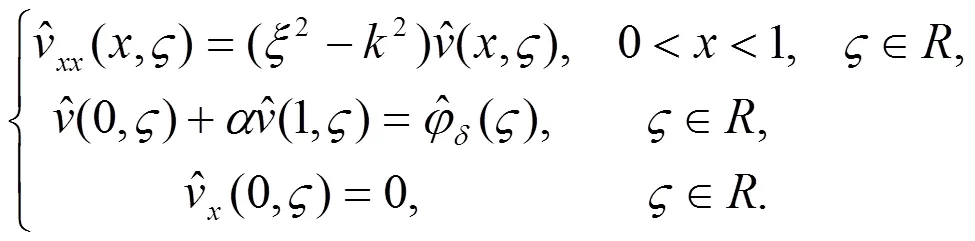
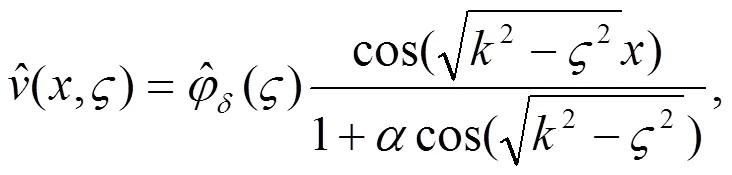
2 收敛性估计

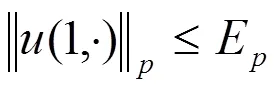
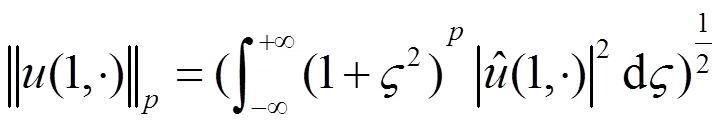
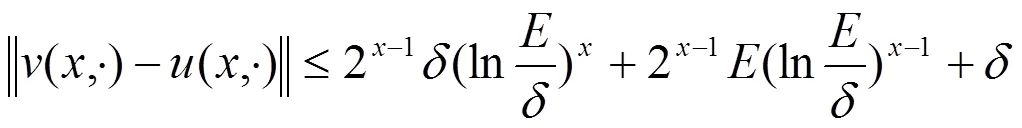
证明:由Parserval等式以及(2.1)和(3.1)的两个假设，可以得到

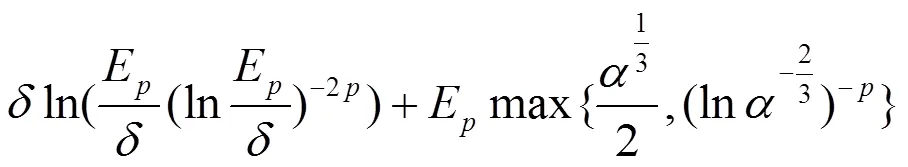
证明:类似于定理1的证明，得到

当

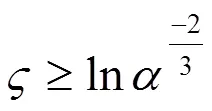
当

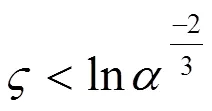
3 数值算例

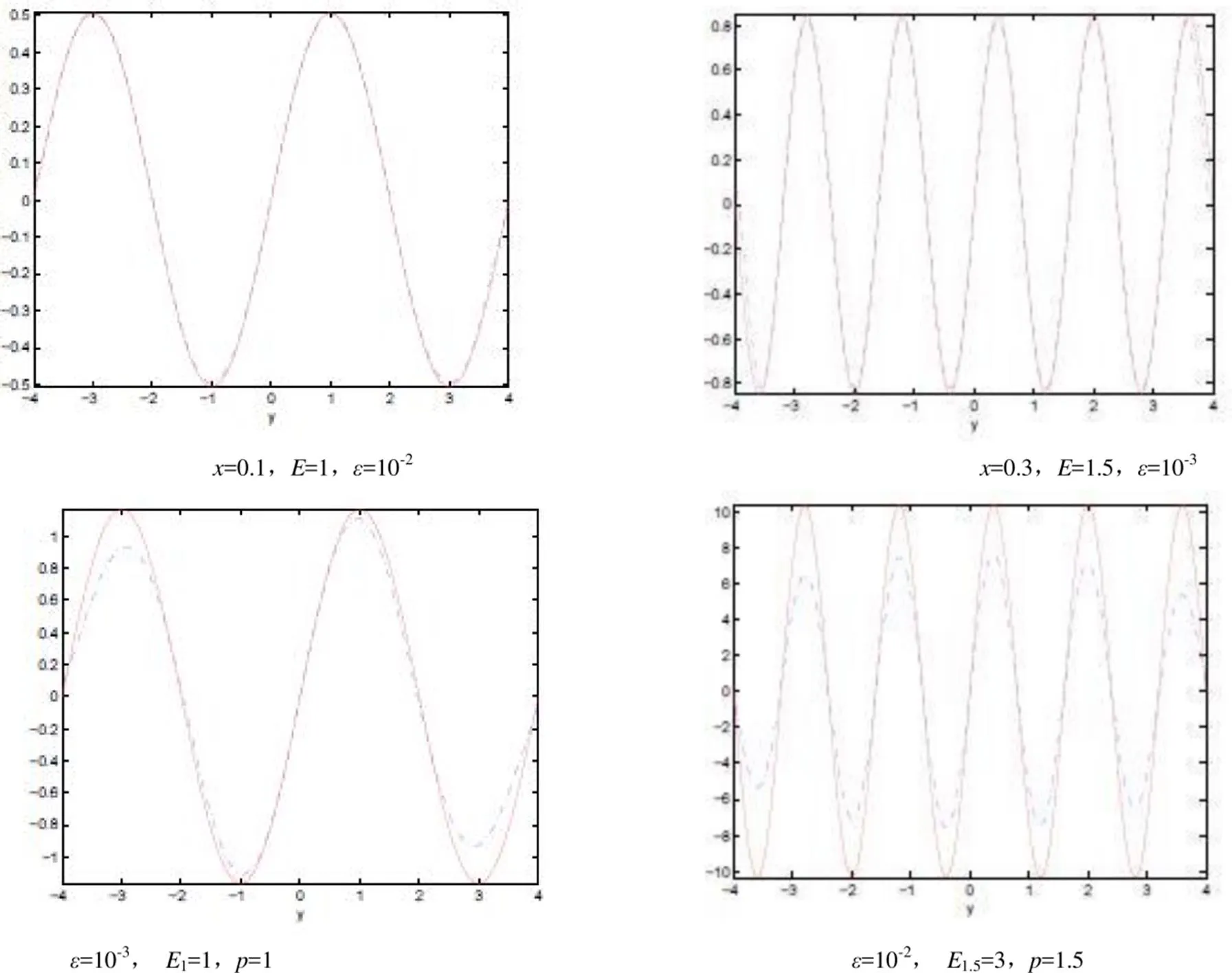
图1 精确解与近似解的误差

[1] Beskos D E. Boundary element methods in dynamic analysis[J].Applied Mechanics Reviews, 1997,50(3):149- 197.

[2] Chen J T, Wong F C. Dual formulation of multiple reciprocity methodfor the acoustic mode of a cavity with a thin partition[J]. Journal of Sound and Vibration, 1998, 217(1) :75-95.

[3] Hrycak T, Isakov V. Increased stability in the continuation of solutions to the Helmholtz equation[J]. Inverse Problems, 2004, 20 (3):697-712.

[4] Hadamard J. Lectures on Cauchy’s problem in linear partial differential equations[M]. New York:Dover Publications, 1953.

[5] 刘继军.不适定问题的正则化方法及应用[M]. 北京:科学出版社, 2005.

[6] Isakov V. Inverse problems for partial differential equations[M]. vol. 127 of Applied Mathematical Sciences. New York :Springer-Verlag, 1998.

[7] Tikhonov A., Arsenin V. Solutions of ill-posed problems[M]. New York:V. H. Winston& Sons, Washington, D.C.: John Wiley & Sons, 1977.

[8] Jin B, Zheng Y. A meshless method for some inverse problems associated with the Helmholtz equation[J]. Comput. Methods Appl. Mech. Engrg., 2006,195 (19-22 ):2270-2288.

[9] Reginska T, Reginski K. Approximate solution of a Cauchy problem forthe Helmholtz equation[J]. Inverse Problems, 2006, 22(3):975-989.

[10] Marin L, Elliott L, Heggs P J, et al. Conjugate gradient-boundary element solution to the Cauchy problem for Helmholtz-type equations[J]. Comput. Mech., 2003,31(3-4):367-377.

Based on the boundary modification regularization method for the Cauchy problem of Helmholtz equations

LIU Li-ping

(School of Computer Science, Gansu Institute of Politics Science and Law, Gansu, Lanzhou 730070, China)

The Cauchy problems for the Helmholtz equations are considered. The problem is ill-posed in the sense that the solution (if exists) does not depend continuously on the given data. In order to obtain a stability approximation solution of the problem, it is necessary to employ some regularized techniques. Furthermore, we use the boundary modification regularized method to solve the Cauchy problems for Helmholtz equations and give the convergence estimates. Finally, the numerical examples show that the proposed numerical method works effectively.

Helmhotz equation; Cauchy problem; ill-posed problem; the boundary modification regularization method; error estimate

O175.8

A

10.3969/j.issn.1674-8085.2012.04.005

1674-8085(2012)04-0021-04

2012-04-22；

2012-05-20

刘利平(1984-)，女，湖南株洲人，助教，硕士，主要从事偏微分方程研究(E-mail: liulipinglele@163.com).