基于高维正态积分的串联结构系统可靠性研究

马永亮，曲先强，崔洪斌，石德新

(哈尔滨工程大学 多体船技术国防重点学科实验室，黑龙江 哈尔滨 150001)

结构系统可靠性的最基本形式可以分为串联系统和并联系统.根据一阶可靠性方法(FORM)，Hohenbichler提出串联系统和并联系统可靠性都可以表示为高维正态积分的形式［1］.通过对高维正态积分的求解可以获得结构系统的失效概率.然而，由于高维正态概率函数的不可积性，该问题的求解必须借助于各种数值方法［2］.直接进行数值积分是一种最基本的方法，Milton采用改进 Simpson方法［3］，Drezner采用一种特殊的 Gauss-Hermite 法进行高维正态积分的求解［4］.Milton方法对于6维以上的积分，Drezner方法对于10维以上的积分很难实现［3，5］.因此，高维正态积分近似方法的研究愈加重要.Hohenbichler和Rackwitz提出了FOMN方法，FOMN方法受积分维数和相关系数的影响很大［1］;Tang和Melchers提出了I-FOMN方法和G-FOMN方法，对FOMN方法的计算精度进行了改进，其中GFOMN方法的计算精度较高［6］;Pandey提出了PCM方法［7］;Mori和Kato指出G-FOMN方法和PCM方法在进行串联系统可靠性计算时误差可高达50%［8］;Yuan和Pandey后来提出了PCM方法的改进方法IPCM方法［9］.这些近似方法虽然计算方便H，但计算误差很大有时甚至是错误的，所以仍然需要寻求计算效率高、计算精度好的方法.针对这一需要，本文采用基于 Halton 序列［10］和数论网格［11］的准 Monte Carlo方法求解高维正态积分，通过比较认为基于数论网格的准Monte Carlo方法计算精度高.从而提出一种串联结构系统可靠性计算方法，并将该方法和其他方法进行了比较.

1 高维正态积分求解的准Monte Carlo方法

1.1 高维正态积分表达式及积分变换

式中:

用于串联结构系统可靠性计算的高维正态积分表达式为

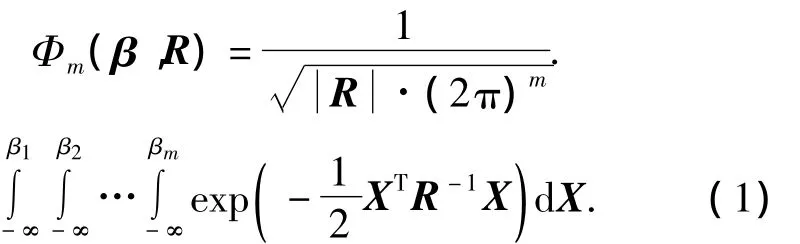
式中:m为失效模式的个数，也是积分的维数;β=(β1，β2，…βm)为各个失效模式的可靠性指标;X=［x1x2… xm］T为积分变量，R(m×m)为失效模式之间的相关系数矩阵.

高维正态积分Φm(β，R)需要采用积分变换和数值方法进行求解.由于Φm(β，R)的积分域为半无限域，很难进行积分求解，所以进行合适的积分变换是必要的.通过以下3步变换可以将高维正态积分转化为单位超立方域内的高维积分［12］.

1)对 R(m ×m)进行 Cholesky分解［13］，得到下三角矩阵L，并令X=LY，式(1)可以表示为

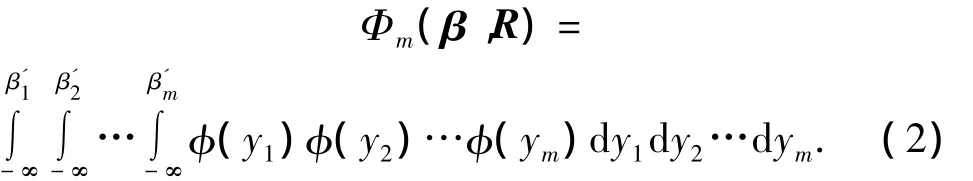
式中:φ(y1)为标准正态分布概率密度函数，为积分上限 β＇i

2)使用变换，yi=Φ－1(Zi)，式(2)可以写作:

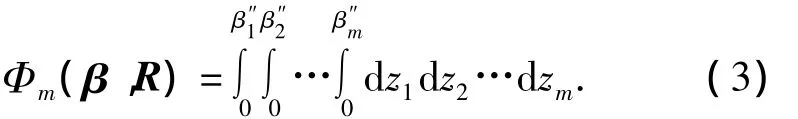
3)使用变换Zi=wi·，式(3)可以写为

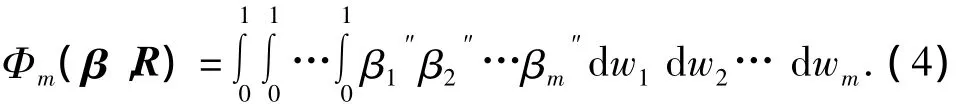
1.2 高维积分的准Monte Carlo求解方法

对于高维积分的求解，像Monte Carlo方法一样，准Monte Carlo方法的计算误差与积分维数和积分区域无关，准Monte Carlo方法可以得到真实误差，且已经证明这个误差要比概率误差小［11］.所以选用准Monte Carlo方法进行高维正态积分的求解.式(4)可以写为

采用准Monte Carlo方法，式(5)的估计值为［14］

估计值的方差为［14］

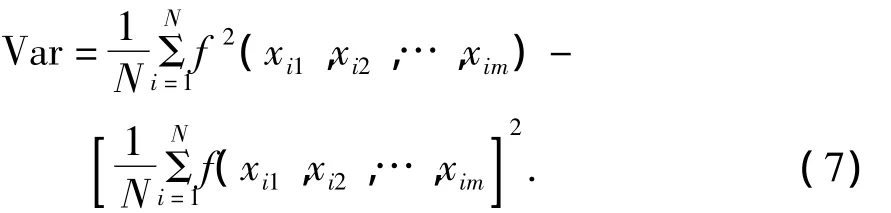
式中:(xi1、xi2、…、xim)表示积分区域上的m维确定性点，采用哈顿序列和数论网格点来表示.

1.2.1 哈顿序列

哈顿(Halton)序列［10］于 1960年提出，最初用于一维均匀序列的产生，后来被扩展到了高维情况.

一维Halton序列的产生可以分成2步:

1)将非负整数i转化为Pk进制的整数，表示为

2)将Pk进制的整数反转变为Pk进制的小数，再转化为十进制的小数，表示为

多维Halton序列可以通过产生多个一维序列获得，随着积分维数的变化Pk需要取不同的素数.对于m个随机变量的积分，取N个积分点的情况，首先选取前m个素数，产生一维Halton序列，然后再形成m维Halton序列，表示为

式中:i=0，1，…N －1.

1.2.2 数论网格法(Lattice method)

数论网格法［11］最早由柯洛波夫(Korobov)于1959年提出.对于m个随机变量的积分，取N个网格点的情况，最简单的单位超立方网格定义为

式中:{·}表示取小数部分，(a1，a2，…，am)称为最优系数.

按照定义，网格点的产生主要与最优系数(a1，a2，…，am)有关，最优系数(a1，a2，…，am)的选取与积分计算结果的误差有关，式(6)的数论网格法(Lattice method)积分可以表示为

式中:E为误差项.

数论网格法(Lattice method)特别适用于被积函数为周期函数的情形，对于被积函数不是周期函数的情况，需要通过Fourier展开表示为周期函数.所以误差项是由Fourier级数形式表示的，最优系数(a1，a2，…，am)要满足误差项 E 最小的原则，最优系数可以参考文献［15］来选取，本文按照Joe提出的准则进行最优系数的选择［16］.

1.3 计算精度比较

1.3.1 Benchmark 解

在各个失效模式的可靠性指标相等以及失效模式之间的相关系数相等的情况下，即βi=β，rij=r，高维正态积分函数Φm(β，R)可以被化简为一维积分，表达式为［17］

将这个特殊的精确解作为Benchmark解，用来评估本文所提出的方法的准确性.

1.3.2 两种方法的比较

根据准Monte Carlo方法，高维正态积分的求解主要与3个因素有关:样本数量、可靠性指标和相关系数.为了研究本文提出方法的准确性，采用2个指标作为衡量标准:1)结果的变异系数(coefficient of variation，Cov);2)结果的误差.其中，变异系数表示结果的收敛快慢，变异系数越小表示结果的收敛程度越好;误差表示结算结果的准确性，误差越小说明结果越准确.

根据式(6)和式(7)，结果的变异系数定义为

根据式(6)和式(13)，结果的误差定义为

采用1 000 000个样本，按照式(14)、(15)2种标准进行了计算，计算结果如图1～2所示.

从结果的收敛速度来说，3种方法的收敛速度随可靠性指标的增加而变快，随相关系数的增大而减慢，Halton序列方法对结果的收敛速度影响不大，数论网格方法(Lattice method)的收敛速度远大于随机抽样.

图1 不同β和r时的Cov计算结果Fig.1 The result of Cov for differentβ and r

从结果的准确性来看，3种方法的准确性都随可靠性指标的增加和随相关系数的增大而降低.本文提出的2种准Monte Carlo方法的准确性远高于随机抽样的一般Monte Carlo方法，其中数论网格方法(Lattice method)的精度可以控制在3%以内，Halton序列的精度可以控制在10%以内.

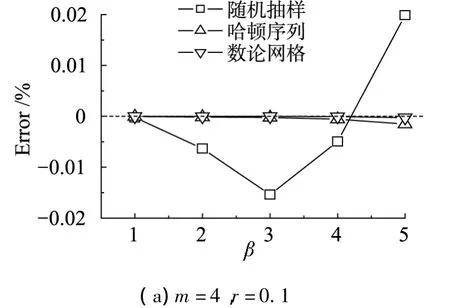
图2 不同β和r时的Error计算结果Fig.2 The result of Error for different β and r

2 串联结构系统的可靠性计算

在结构系统中任何一个模式失效都有可能导致整个结构系统失效，则称这种体系为串联系统.一般地，由m个失效模式组成的串联系统，通常用图3所示的符号表示［17］.

图3 串联结构系统示意图Fig.3 Sketch of the series structural system

对于串联体系，设 F1，F2，…，Fm，表示各个模式的失效事件，则该系统的失效概率为

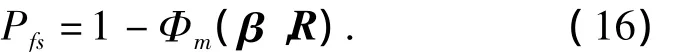
本文提出的2种准Monte Carlo方法中，数论网格法(Lattice method)无论在收敛速度还是在计算精度上都比Halton序列方法好，在以后的计算中都采用数论网格法.

根据式(13)和式(16)，串联结构系统的失效概率可以表示为

式(17)可以用来评估串联结构系统可靠性数值方法计算的准确性.采用式(18)来计算近似方法的误差.

采用以上评估方法，将本文提出数论网格方法(Lattice method)和计算串联结构系统可靠性方法中的 G-FOMN 法［6］、PCM 法［7］、IPCM 法［9］以 及Equivalent components法［18］进行了比较.为了研究可靠性指标 β和相关系数 r的影响，取 m=20，1 000 000个样本进行计算，计算结果和其他方法的比较如图4所示.

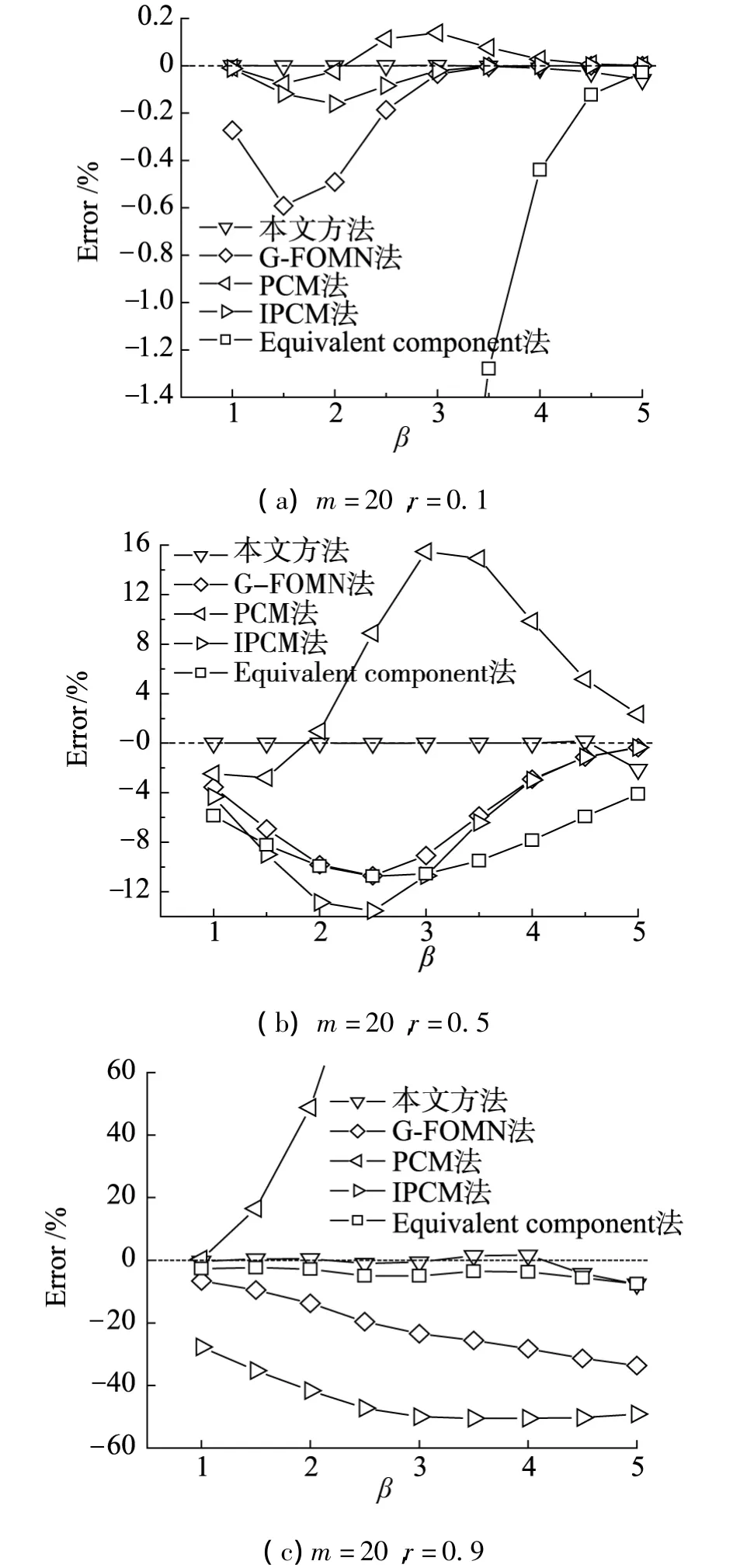
图4 不同β和r时的计算结果比较Fig.4 Comparison of the results for different β and r

为了研究积分维数m和相关系数的影响r，取β=4，1 000 000个样本进行计算，计算结果和其他方法的比较如图5所示.为了研究可靠性指标β的影响，取r=0.9，1 000 000个样本进行计算，计算结果和其他方法的比较如图5(c)和图6所示.

从图4可以看出，在 r=0.1和 r=0.5时 GFOMN法、PCM法、IPCM法的计算误差随可靠性指标的增大经历了一个由小到大再变小的过程，在r=0.9时这3种方法的计算误差随可靠性指标的增大而增大;在r=0.5时Equivalent components法的计算误差随可靠性指标的增大经历了一个由小到大再变小的过程，在r=0.1和r=0.9时Equivalent components法的误差随可靠性指标的增大而减小;本文提出方法的计算误差随可靠性指标的增大而增大.

从图5可以看出，在r=0.1时本文方法和其他4种方法的计算误差都随积分维数的增大而增大;在r=0.5和在r=0.9时本文提出的方法、G-FOMN法、IPCM法的计算误差随积分维数的增大而增大，而PCM法和Equivalent components法的计算误差随积分维数的增大而减小.

从图5(c)和图6可以看出，在r=0.9时，不论积分维数取值是多少，本文提出的方法和其他4种方法的计算误差都随可靠性指标的增大而增大.

综合所有的计算结果来看，本文提出的数论网格方法(Lattice method)的计算误差较小，计算精度远高于其他4种方法.

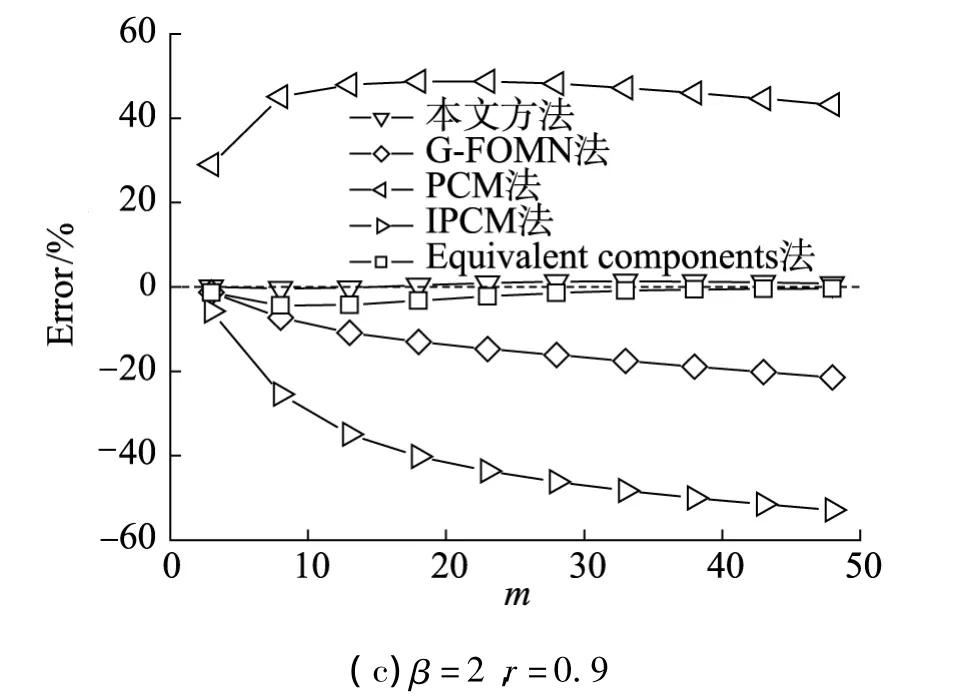
图5 不同m和r时的计算结果比较Fig.5 Comparison of the results for different m and r

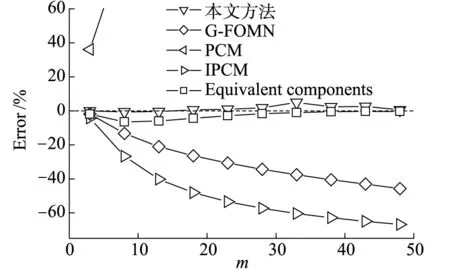
图6 β=4，r=0.9时的计算结果比较Fig.6 Comparison of the calculation results for β =4，r=0.9

3 计算实例

我国现行的《潜水系统和潜水器入级与建造规范》，给出了耐压环肋圆柱壳结构的5种校核公式［19］.大量的潜水器结构可靠性研究文献将这5种校核公式作为失效模式的极限状态方程.

失效模式1 肋骨跨中壳板纵剖面内中面周向应力强度不足，表达式为:G1=σs－.

失效模式2 肋骨跨端板壳内表面纵向应力强度不足，表达式为:G1=σs－σ1.

失效模式3 肋骨应力强度不足，表达式为:G3=σs－σf.

失效模式4 相邻肋骨间壳板失稳.表达式为:G4=Pcr－P.

失效模式5 舱段整体失稳，表达式为:G5=－P.其中，符号的具体涵义以及随机变量的分布和特征参数见文献［13］.首先通过一次二阶矩方法，计算出各个失效模式的可靠性指标，再计算出失效模式之间的相关系数，然后通过式(15)求解系统的失效概率.各个失效模式的可靠性指标如表1所示，失效模式之间的相关系数如表2所示.

表1 各失效模式的可靠性指标Table 1 Reliability index of every failure modes

表2 各个失效模式之间的相关系数Table 2 The correlation among failure modes

将数论网格方法(Lattice method)的计算结果和Drezner方法［4］进行了比较，比较结果如表3所示.从表3可以看出本文方法和Drezner方法的计算结果很接近，说明该方法的计算精度较高.

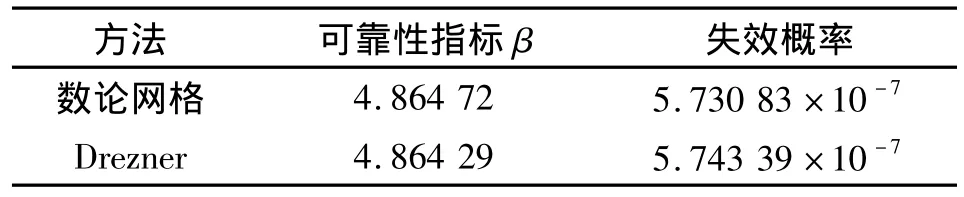
表3 计算结果的比较Table 3 Comparison of the calculation results

4 结束语

本文提出一种求解高维正态积分的准Monte Carlo方法，并将此方法用于串联结构系统可靠性的计算中.与其他近似方法相比较，本文提出的方法具有与积分维数无关、受可靠性指标和相关系数影响不大的特点.计算实例表明，本文提出的方法计算精度高，计算结果稳定，适应性广.同时，本文提出的高维正态积分计算方法也适用于并联系统可靠性的计算.

［1］HOHENBICHLER M，RACKWITZ M.First-order concepts in system reliability［J］.Structural Safety，1983，1:177-188.

［2］贡金鑫.一类多维正态积分的近似解法［J］.西安建筑科技大学学报，1996，28(1):52-56.GONG Jinxin.Approximate solution for a class of multi-normal integral［J］.Journal of Xi’an University of Architecture and Technology，1996，28(1):52-56.

［3］MILTON R C.Computer evaluation of the multivariate normal integral［J］.Technometrics，1972，14(4):881-889.

［4］DREZNER Z.Computation of the multivariate normal integral［J］.ACM Transactions on mathematical Software，1992，18(4):881-889.

［5］马永亮，曲先强，崔洪斌，等.基于数值积分方法的潜水器耐压圆柱壳结构系统可靠性研究［C］//黑龙江省造船工程学会学术年会，哈尔滨，中国，2010:92-96.

［6］TANG L K，MELCHERSR E.Improved approximation for multi-normal integral［J］.Structural Safety，1987，4:81-93.

［7］PANDEY M D.An effective approximation to evaluate multinormal integrals［J］.Structural Safety，1998，20:51-67.

［8］YASUHIRO M，TERUYUKI K.Multi-normal integrals by importance sampling for series system reliability［J］.Structural Safety，2003，25:363-378.

［9］YUAN X X，PANDEY M D.Analysis of approximations for multi-normal integration in system reliability computation［J］.Structural Safety，2006，28:361-377.

［10］GLASSERMAN P.Monte Carlomethods in financial engineering［M］.Beijing:Higher Education Press，2008:293-297.

［11］宫野.计算物理［M］.大连:大连工学院出版社，1987:275-292.

［12］GENZ A.Numerical computation of multivariate normal probabilities［J］.Journal of Comput Graph Stat，1992，1:141-150.

［13］马永亮.考虑腐蚀影响的潜艇结构可靠性研究［D］.哈尔滨:哈尔滨工程大学，2009:14-18.MA Yongliang.Reliability assessment of submarine structure considering corrosion［D］.Harbin:Harbin Engineering University，2009:14-18.

［14］DAVISP，RABINOWITZP.数值积分法［M］.冯振兴，伍富良，译.北京:高等教育出版社，1986:235-238.

［15］冯康.数值计算方法［M］.北京:国防工业出版社，1978:82-84.

［16］JOE S，SLOAN IH.Implementation ofa lattice method for numerical multiple integration［J］.ACM Transactions on Mathematical Software，1993，19(4):523-545.

［17］何水清，王善.结构可靠性分析与设计［M］.北京:国防工业出版社，1993:208-216.

［18］GOLLWITZER S，RACKWITZ R.Equivalent components in first-order system reliability［J］.Structural Safety，1983，5(2):359-366.

［19］中国船级社.潜水系统和潜水器入级与建造规范［S］.北京:人民交通出版社，1996:32-42.