词语同义关系的模糊矩阵描述

贾 璐

［责任编辑:丁秀菊］

物质世界是普遍联系着的，因此客观事物之间就存在着各种各样的关系。在这些关系中，有些关系的界限是很明确的，比如同学关系、师生关系、兄弟关系等，而更多的是一些界限不明确的关系，比如朋友关系、作物生长与土壤的关系、经济发展与产业结构的“协调关系”、父亲与子女间相貌的“相像关系”等等。我们把界限明确的关系称为普通关系，而把界限不明确的关系称为模糊关系①陈水利、李敬功、王向公:《模糊集理论及其应用》，北京:科学出版社，2005年，第59页。。模糊关系不仅大量存在于我们的现实生活中，而且也存在于一些语言现象当中。因此，对具有各种性质的模糊关系进行深入的探讨，并设法以精确的形式描述它，是非常具有理论意义和实践价值的。

一、词语同义关系的模糊性及其矩阵表示

模糊关系体现的是关系外延的不确定性，语言中词语的同义关系就具有这样的特征。词语的同义关系是靠同义词来体现的，《现代汉语词典》对“同义词”的解释是:“意义相同或相近的词”。但是，怎样才算“意义相同或相近”，意义究竟相近到什么程度才能叫做同义词，这些都是不确定的。换句话说，词语的同义关系具有模糊性。

我们把具有同义关系的词语所形成的集合称为同义聚合体。如果两个词语彼此之间毫无关系，那它们就被排除在同义聚合体之外;其余所有的进入同义聚合体中的词语，相互之间具有的同义关系都应有一种程度上的不同。其中，等义词之间具有的同义关系程度最高。用模糊集合论的观点来表述就是:词语之间所具有的同义关系是一种模糊关系，刻画这种关系不是要简单地区分每组词语是否具有同义关系，而是要确定词语彼此之间具有同义关系的程度如何。下面我们给出模糊关系在数学中的精确定义:

对于同义关系而言，词语之间具有同义关系的程度就是词语对同义关系的隶属度，它的取值为单位区间［0，1］。该隶属度体现的是同义词之间的相似程度，所以我们把它称为同义词间的相似系数，用r②此处的r指词语甲和乙对同义关系的隶属度。来表示。若两个词语之间完全没有同义关系，则r=0;若两个词语完全同义，是意义相互之间的一致程度达到百分之百的等义词，则r=1。大多数同义词是同中有异的，它们之间的相似系数应该介于0和1之间。

词语的同义关系是语言词义关系中十分重要的一种，对同义关系进行深入研究有助于我们更好地掌握一种语言的词汇系统。由以上论述可知，词语之间的同义关系是一种模糊关系，与其他模糊关系不同，词语的同义关系具有数学上十分重要的两个特点:(1)词语的同义关系具有自反性。所谓自反性是指对某一词语而言，它与自身是百分之百同义的。(2)词语的同义关系具有对称性。即对于两个同义词语甲和乙，甲与乙的相似程度等于乙与甲的相似程度。

模糊数学中将具有自反性和对称性的模糊关系称为模糊相似关系。为了精确地描述同义词语之间的这种关系，并把它们直观地表示出来，我们需要借助于一种数学工具。这样，专门用来刻画模糊关系的模糊矩阵便成为了我们选择的对象。

有限论域上的模糊关系都可以用模糊矩阵来表示，每个模糊矩阵都代表一定的模糊关系。③苗东升:《模糊学导引》，北京:中国人民大学出版社，1987年，第63页。在描述普通关系的布尔矩阵中，元素的取值为集合0，{}1，而在模糊矩阵中，元素的取值需扩展为区间［0，1］，即如果对任意的 i≤m 及 j≤n，都有 rij∈［0，1］，那么矩阵 M=［rij］m×n就称为的模糊矩阵④王新洲、史文中、王树良:《模糊空间信息处理》，武昌:武汉大学出版社，2003年，第13页。。在有限论域中，给定一个模糊关系，就惟一确定一个模糊矩阵;反之，给定一个模糊矩阵，也惟一确定一个模糊关系。模糊关系与模糊矩阵是一一对应的。

鉴于词语同义关系的上述两个特点，我们用来对其进行描述的模糊矩阵也应满足相应条件。由于同义关系的自反性，即词语自身与自身完全相似，相似系数为1，这就要求矩阵中行标与列标相等的元素rii=1;由于同义关系的对称性，词语间的相似程度不因词语相互顺序的改变而改变，故而要求矩阵中行标与列标互换后得到的元素仍相等，即rij=rji，这样势必要求该矩阵是一个行数与列数都相等的方阵。我们将能够体现模糊关系自反性与对称性的矩阵称为模糊相似矩阵，词语的同义关系就可以用模糊相似矩阵来予以形式化的描述。由上可知，模糊相似矩阵的实质是主对角线上元素恒为1的对称方阵，其形式如下:

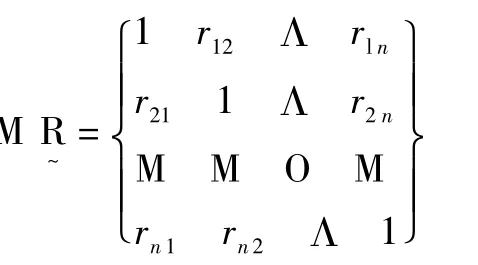
模糊相似矩阵中的元素其实就是同义词之间的相似系数，只要我们能够确定这些相似系数，那么同义聚合体中各个成员彼此间的亲疏远近关系就可以一目了然地呈现在模糊相似矩阵这个平面当中。这不仅可以深化我们对同义词本身词义的认识，而且可以为计算机进行同义词的信息处理提供方便。为了达到这个目的，我们来尝试确定一种同义词间相似系数的方法。

二、同义词间相似系数的确定方法

相似性科学是现代自然科学中的一门新兴理论，主要以相似性和相似系统为研究对象。语言中的同义词彼此之间就具有相似性。如果我们将同义聚合体中的一个成员视为一个系统，那么就可以将相似性科学中的有关方法引入到同义词的相似性研究中。

系统相似度的数值度量包括组成要素的数量相似度量和特性相似度量两方面。实现对相似系统要素特性的数值度量，需要获取每一个特性的特征值，相似系统间对应要素特性的特征值的比例系数就反映了系统要素特性的相似程度①周美立:《相似性科学》，北京:科学出版社，2004年，第38页。。由于语言的特性都是用文字来描述的，不能像物理量那样具体测量它的特征值，所以很难进行相似系统要素特性的定量分析。下面是系统要素数量相似度的计算方法:

设两个系统 A 和 B，若系统 A 有 K 个组成要素:a1，a2，…，aK，系统 B 有 L 个组成要素:b1，b2，…，bL，则系统A和B可以分别表示为它们对应的组成要素的集合:

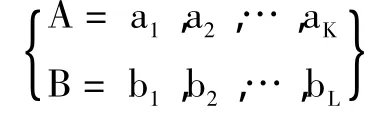
如果A、B这两个系统中存在相似要素，那么系统A与B即为相似系统，设两系统间相似要素的个数为N。我们把系统A、B间相似要素的数量与系统A、B间共有且不重复要素数量的比值，称为系统要素数量的相似度，记为Qn，用公式表示为:

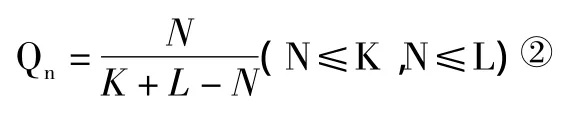
② 周美立:《相似性科学》，第66页。

由上式可见，在系统A、B中要素数量一定的条件下，系统间相似要素的数量越多，相似度越大。

相似性科学中关于系统相似程度的计算方法适用于一切相似系统，我们可以利用它来量化同义词之间的相似程度。但要对词义具有相似性的同义词进行相似程度的计算，首先必须对同义词本身进行组成要素的分析。现代语义学界提出的义素分析法为我们分析词义的内部构成提供了一种可资借鉴的方法。义素分析法对处于同一语义场内的各个义位进行对比，然后找出它们所包含的义素。它“将触角伸到了词义的微观世界，破天荒地发现了词义的下义单位——义素，从而在追求词义分析的精细化、科学性的方向上迈出了极为坚实、极为可喜的一步，为词义的分析开辟了一片新天地。”③曹炜:《现代汉语词义学》，上海:学林出版社，2001年，第90页。

从语义学的观点来看，同义词之间的相似，实际上是不同词语中构成同义关系的义位之间的相似。我们可以将一个义位视作一个系统，该系统的组成要素即为义素。由于义素是由文字表达的，它的特征值无法精确测量，因此我们只从义素的数量分析入手，将两个同义义位中的义素的数量相似度作为具有该义位的同义词之间的相似系数，这是鉴于语言的特殊性而在方法上做出的选择。那么怎样以义素分析法为中介来确定同义词之间的相似系数呢?

设词语X和Y为某一同义聚合体中的任意两个成员，若X、Y为单义词，则它们只有一个义位，只需分别对其进行义素分析即可;若X、Y为多义词，则它们有多个义位，做义素分析时我们只选取其中对应的具有同义关系的两个义位。这些构成同义关系的义位可以聚合形成同义语义场。设在该语义场中存在任意两个义位A和B，分别对其进行义素分析，可以得到描写该义位的一系列语义特征，也即义素。因为义位是义素的聚合体，是一束语义特征的集合，因此，若义位A的义素个数为K，义位B的义素个数为L，则义位A、B可分别表示为以下集合:

同义词是同中有异的，所以在对义位A、B进行义素分析后得到的这一系列义素中肯定存在相同的义素，我们设二者相同的义素个数为N。根据相似性科学中提出的方法，义位A与义位B中义素数量的相似程度，也即同义词语X与Y的相似系数为:

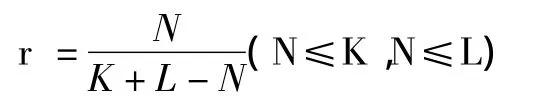
同义词间的相似系数即为词语对同义关系的隶属度，它的取值范围是0≤r≤1。对于构成同义关系的两个义位A与B而言，若r越接近于1，则义位A与义位B具有同义关系的程度越大，包含该义位的同义词之间的差异就越小;反之，若r越接近于0，则义位A与义位B具有同义关系的程度越小，包含该义位的同义词之间的差异就越大。r反映的是两个同义词之间的相似程度。

由此可见，义素分析法是量化语言信息的桥梁，它将义位分解为若干义素的集合，在语言信息的数量化过程中起到了中介的作用，使相似性科学中的有关方法得以在同义词的研究中顺利应用，从而为词语同义关系的矩阵描述提供了有力保障。

三、词语同义关系的矩阵描述举例

词语的同义关系是一种模糊关系，套用前面模糊关系的数学定义，词语的同义关系可以表述如下:设彼此间具有同义关系的词语所构成的同义聚合体为论域U，其中任意两个词语之间具有的同义关系就是U自身的笛卡尔积U×U的一个模糊子集。用来描述词语同义关系的矩阵为具有自反性和对称性的模糊相似矩阵，矩阵中的元素即为彼此间具有同义关系的词语之间的相似系数。当我们确定出这些相似系数之后，就可以对词语的同义关系进行矩阵描述了。

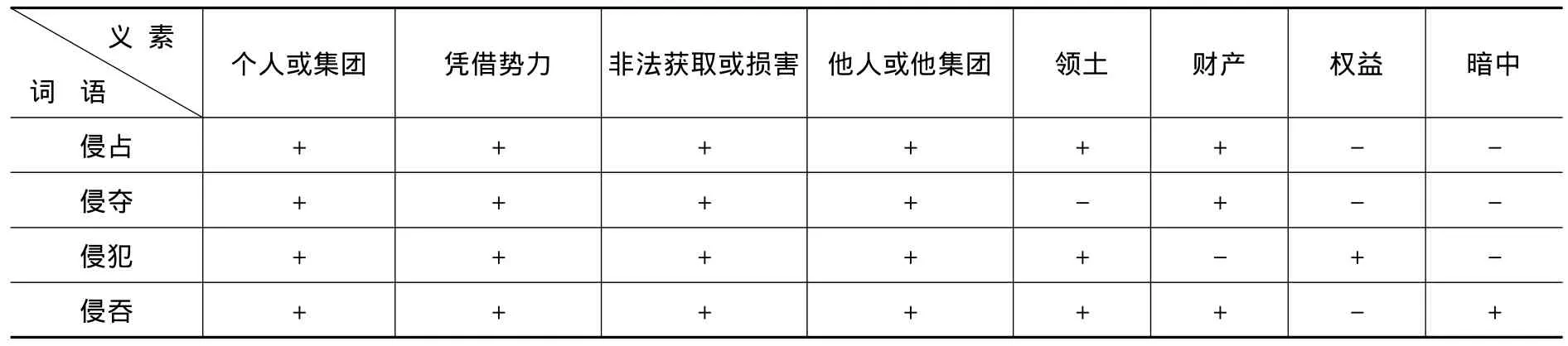
根据义素分析法的步骤，首先需要对被分析词语的义位确立一个语义场，然后在该场内进行分析比较，找出组成各义位的义素，最后以序列或图表的形式表示出来。我们此处不准备具体探讨如何进行义素分析，仅想以现有的研究成果为例来说明问题。“侵占”、“侵夺”、“侵犯”、“侵吞”4个同义词，构成同义关系的义位进行义素分析后，它们的义位、义素关系可用图表的形式表示如下(其中“+”表示某义位包含有该义素，“－”表示某义位不含有该义素):①曹炜:《现代汉语词义学》，第110页。

个人或集团 凭借势力 非法获取或损害 他人或他集团 领土 财产 权益 暗中侵占++++++－－侵夺++++－+－－侵犯+++++－+－侵吞++++++－+

这里论域U= {侵占，侵夺，侵犯，侵吞 }，聚合形成同义语义场的是这4个词语中构成同义关系的义位。表中任意两个词语之间所具有的同义关系就是U上的一个模糊关系，它是U自身的笛卡尔积U×U的一个模糊子集，笛卡尔积U×U=＜侵占，侵占＞，＜侵占，侵夺＞，＜侵占，侵犯＞，＜侵占，侵吞＞，＜侵夺，侵占＞，＜侵夺，侵夺＞，＜侵夺，侵犯＞，＜侵夺，侵吞＞，＜侵犯，侵占＞，＜侵犯，侵夺＞，＜侵犯，侵犯＞，＜侵犯，侵吞＞，＜侵吞，侵占＞，＜侵吞，侵夺＞，＜侵吞，侵犯＞，＜侵吞，侵吞＞。r用来表示同义词之间的相似系数，根据同义关系的自反性，有r(侵占，侵占)=r(侵夺，侵夺)=r(侵犯，侵犯)=r(侵吞，侵吞)=1;根据同义关系的对称性，有r(侵占，侵夺)=r(侵夺，侵占)，r(侵占，侵犯)=r(侵犯，侵占)，r(侵占，侵吞)=r(侵吞，侵占)，r(侵夺，侵犯)=r(侵犯，侵夺)，r(侵夺，侵吞)=r(侵吞，侵夺)，r(侵犯，侵吞)=r(侵吞，侵犯)。在用来描述所有词语两两之间的同义关系的模糊相似矩阵中，待定元素为后6组具有对称性特点的同义词之间的相似系数。在确定它们的具体数值之前，我们先把上表各词语中构成同义关系的义位表示为它们对应义素的集合:

侵占:{个人或集团，凭借势力，非法获取或损害，他人或他集团，领土，财产}

侵夺:{个人或集团，凭借势力，非法获取或损害，他人或他集团，财产}

侵犯:{个人或集团，凭借势力，非法获取或损害，他人或他集团，领土，权益}

侵吞:{个人或集团，凭借势力，非法获取或损害，他人或他集团，领土，财产，暗中}

这样，我们就可以清楚地看出每个词语的义位所具有的义素个数及与其他词语的义位相同的义素个数。利用相似性科学中提出的计算公式，上述4个同义词语两两之间的相似系数分别为:

将以上得出的所有的相似系数以矩阵的形式来表示，就得到了描述同义词语“侵占”、“侵夺”、“侵犯”、“侵吞”两两之间关系的模糊相似矩阵:

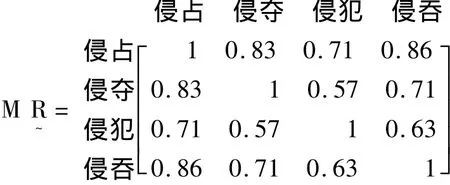
从这个矩阵中我们可以看出，处于同一个同义聚合体中的各个词语，它们相互之间的聚合并不在同一平面上，而是可以分为不同的层次。也就是说，词语相互之间具有同义关系的程度是不同的。其中，词语“侵占”与“侵吞”的相似程度最大，为0.86;词语“侵犯”与“侵夺”的相似程度最小，为0.57。本例中所有词语两两之间相似系数的顺序依次为:r(侵占，侵吞)≈0.86＞r(侵占，侵夺)≈0.83＞r(侵占，侵犯)=r(侵夺，侵吞)≈ 0.71 ＞ r(侵犯，侵吞)≈ 0.63 ＞ r(侵夺，侵犯)≈ 0.57。所有的相似系数都大于0.5，说明这些词语彼此相同的程度要大于彼此相异的程度，这也正说明了同义词是同中有异，而且是大同小异的。

需要指出的是，确定词语相似系数的方法，是建立在对词语进行合理的义素分析基础之上的。虽然义素分析法还存在着这样那样的缺点，而且也不能适用于所有词语，但是我们不应该就此放弃对义素分析法的利用。我们需要做的，是不断深入对义素分析法的研究，修订、完善它在理论上和实践中的一些不足，使它精确描写词义的优势得以充分发挥，从而为我们进一步探讨词义关系提供保障。同时，如何形式化处理模糊语言现象，让计算机能够更好地识别这些信息并为我们的语言研究服务，是一个需要不断探索的问题。