Be掺杂浓度对ZnBeO体系电子结构的影响

张 牛，刘亚明，张文庆，侯振雨

（1．中原工学院，郑州450007；2．河南科技学院，新乡453003）

Be掺杂浓度对ZnBeO体系电子结构的影响

张 牛1，刘亚明2，张文庆2，侯振雨2

（1．中原工学院，郑州450007；2．河南科技学院，新乡453003）

采用基于密度泛函理论的第一原理方法，计算了Zn16－nBenO16掺杂体系所有的652种不同几何构型．结果表明：掺入ZnO的Be原子均匀分散，不出现聚集，与实验中没有观测到ZnO和BeO出现相分离这一现象吻合；掺杂浓度为25%、50%和75%时，掺杂的Be原子均匀对称地分布在32个原子组成的超原胞中，此时体系处于最稳状态；优化Be浓度从0到100%的掺杂体系几何结构，获得的晶格参数与实验值吻合较好，符合Vegard’Law拟合带隙曲线，得到的禁带弯曲系数b为5．76 eV．

Be掺杂；ZnO；第一原理．

ZnO是一种新型的直接宽带隙纤锌矿半导体材料，室温下禁带宽度达3．37 e V，激子结合能60 me V，具有低介电常数和高化学稳定性等特点．这使得Zn O广泛应用于发光二极管、光电探测器以及生物传感器等领域［1－3］．

由于纯净Zn O仅在紫外波段发光，要想实现Zn O在光电子器件中的广泛应用，则需要对其进行带隙调制．这是目前Zn O应用方面遇到的一大困难，也是研究热点．为了实现可见区发光，则要减小其带隙；为了获得紫外短波光谱和制造量子阱、超晶格，则要增大其带隙．虽然带隙仅为2．3 e V［4］的 Cd O 掺入ZnO后能减小其带隙，但是通过调节Cd的掺杂含量，可使ZnO的发光波段从紫外波段红移到蓝光波段甚至绿光波段．由于Cd O是岩盐结构，掺杂Cd后的Zn1－xCdxO在x小于0．62时能保持纤锌矿结构，在x大于0．62时则出现相分离［5］．Mg O和BeO的带隙分别为7．20 e V［6］和10．60 e V［7］，是增宽Zn O带隙的理想材料．Ohtomo A等利用激光分子束衍射方法在Si衬底上制备出了带隙可增宽至3．99 e V的Zn MgO薄膜［8］，但由于 MgO 也是岩盐结构，研 究发现，当Zn1－xMgxO中的 Mg含量x大于0．33时，会引起Zn1－xMgxO中MgO相分离．杜祖亮教授的科研小组从理论上详细研究了Mg掺杂增大带隙的情况，发现掺入的Mg的2p电子态优势明显，导致导带及导带底向高能端移动，且Zn O的4s电子态下降，带隙增宽［9］．和MgO相比，BeO具有和ZnO一样的纤锌矿结构，因此被认为应用潜力巨大，目前也有很多这方面的报道．Khoshman J M 等利用反应溅射在Si（100）衬底上成功生长出了Zn BeO薄膜，而且通过改变Be浓度可以将带隙调宽至7．91 e V，但随后的X－射线衍射谱显示该薄膜是非晶态［10］．Ryu Y R等在采用混合束沉积法（hybrid beam deposition，HBD）制备的ZnBeO薄膜中没有发现Zn O或BeO相分离，而且Be浓度 可 以 从 0 增 加 到 100%［11］．Ding S F 等 和Zheng Y P等借助第一原理详细计算和讨论了ZnBeO的电子结构及光学特性［12－13］，但对掺杂体系的结构信息如掺杂浓度对ZnBeO体系稳定性的影响、Be原子的最稳定占据位置以及在稳定掺杂体系中Be原子易于聚集还是分散等没有加以分析讨论．本文采用基于密度泛函理论的第一原理方法，通过计算0～100%掺杂浓度下Be在不同替位的构型，研究ZnBeO的相关结构信息．

1 计算方法

理想的ZnO属六方纤锌矿结构，其中每个Zn2＋（O2－）位于4个 O2－（Zn2＋）组成的四面体中心，即ZnO晶体由O的六角密堆积和Zn的六角密堆积相互反向套构而成．每个原胞由2个Zn原子和2个O原子共4个原子组成，计算中采用的2×2×2超原胞由16个Zn原子和16个O原子组成，Be掺杂即Be原子替换Zn原子形成ZnBeO合金，如图1所示．

本文采用 Material Studio 4．6中的 CASTEP模块进行计算．CASTEP是一个基于密度泛函理论（DFT）并参考平面波赝势方法的从头量子力学计算程序包，广泛应用于金属、非金属等掺杂半导体电子结构和光学特性的研究［14］，是目前公认的较为精准的计算工具．计算中采用的电子波函数通过平面波基组展开，电子与电子间相互作用的交换关联能由广义梯度近似（GGA）下的PBE泛函来处理，用超软赝势（USPP）方法来描述离子实与价电子间的相互作用势，平面波截断能Ecut取为380 e V，布里渊区的积分使用Monkorst－Park方案中3×3×1的特殊k点网格求和．快速傅立叶变换（FFT）采用Fine（40×40×64），原子间相互作用力收敛标准设为0．3 eV／nm．

2 结果与分析

2．1 Zn O和BeO的电子结构

为研究Be掺入对ZnO的影响，本文首先对ZnO和BeO的晶格结构进行优化．采用前面的参数设置，让晶胞中所有原子在固定截断能和许可基失数目变化的条件下自由弛豫，优化得到的理论值和参考的实验值见表1．从表1可以看出，理论计算的优化结果与实验值吻合较好，误差均在2%以内．计算结果与其他第一原理计算结果也吻合较好，说明我们设置的参数和采用的算法是合理有效的．此后的计算均采用优化后的参数．

图2、图3所示分别是Zn O和BeO的能带结构和态密度．从图2、图3可以看出，导带底和价带定位于布里渊区G点处，即Zn O是直接带隙半导体．计算得出的禁带宽度为0．7 4eV，远低于实验测量值3．37 e V，这是第一原理计算中普遍存在的问题［17］．计算中无论采用LDA还是GGA，对于Zn O而言都高估了Zn 3d能量，造成Zn 3d能量与O 2p能量之间的相互作用变大，使得价带增宽、带隙变窄．

表1 ZnO、BeO优化后的晶格参数a、c及晶胞体积V cell

图3显示BeO的禁带宽度最窄处出现在G点，与ZnO一样．BeO也是一种直接带隙半导体，计算得出的禁带宽度为7．01 e V，低于实验值10．60 e V．由于DFT属于基态理论，低估了禁带宽度，故本计算结果与其他DFT计算结果相一致（文献［18］中禁带宽度为7．56 e V，文献［19］中禁带宽度为7．00 e V）．

2．2 ZnBeO的掺杂结构

本文采用2×2×2共32个原子的超原胞模拟Zn16－nBenO16掺杂体系，其中n值可取1，2，…，16，对应的Be掺杂浓度从0到100%．根据排列组合，该掺杂体系共有216＝65 536种构型．考虑到ZnBeO掺杂体系属于P63mc空间群，该掺杂体系构型可约化为652种．

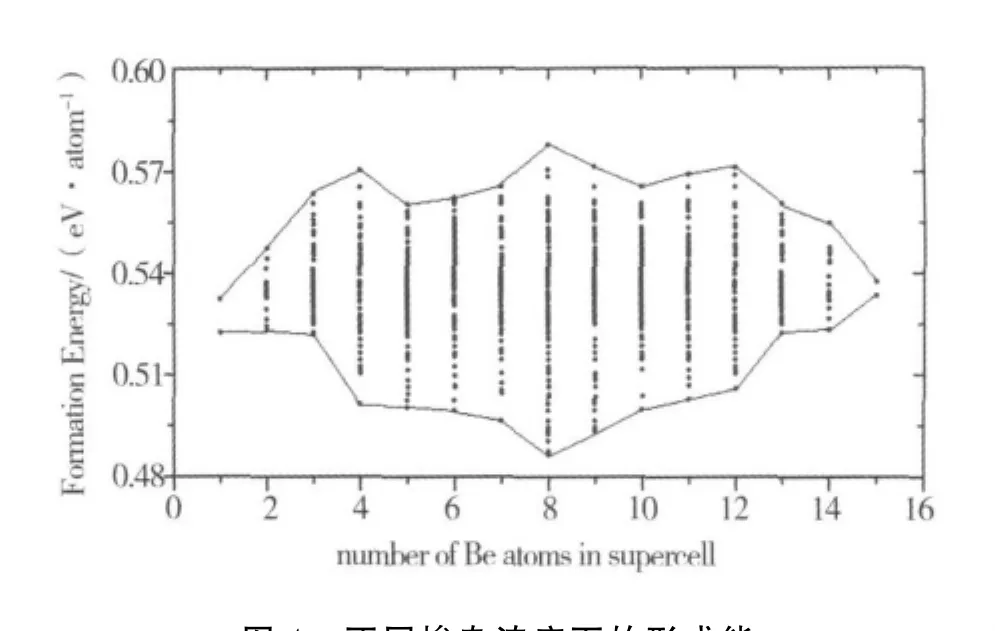
图4 不同掺杂浓度下的形成能

掺杂体系形成能采用Ef＝（16－n）E（ZnO）＋nE（BeO）－E（Zn16－nBenO16）［20］．形成能数值越大，说明成键原子间的相互作用越强，掺杂体系越稳定．1个Be原子替代1个Zn原子后，Be的掺杂浓度为1／16＝6．25%，不同掺杂浓度下的形成能见图4．从图4可清晰地看出：Be掺杂浓度为25%、50%、75%时，即掺杂的Be原子个数为4、8、12时，ZnBeO体系将出现稳定态，形成能分别为0．577 1 eV／atom、0．587 8 e V／atom、0．581 6 e V／atom．与此对应的ZnBeO构型见图1，掺杂的Be原子均匀对称地分散在该超原胞中．对于由4个Zn O双层原子构成的超原胞，高对称掺杂构型为：①每层Zn原子中有1个Be原子替换，Be原子占据四边形锐角顶点位置，侧视呈“之”字型；②每层Zn原子中有2个Be原子替换，Be原子处在四边形的长对角线顶点位置；③每层Zn原子中有3个Be原子替换，Be原子占据四边形锐角顶点位和一个钝角位．与此3种高对称掺杂构型对应的Be原子个数为4、8、12，即掺入ZnO的Be原子不会出现聚集，总是处于“最佳”分散状态．该结论较好地解释了“没有观测到BeO与ZnO出现相分离”这一实验现象．

为了更直观地看出ZnBeO掺杂体系是否易出现相分离，我们又选出相同掺杂浓度的“Be密集掺杂构型”作对比．Be原子个数为4、8、12的掺杂构型分别为：①4个Be原子组成1个四面体；②8个Be原子组成相邻的2层，即2个互相倒置的四面体；③12个Be原子组成相邻的3层原子．相关的吸附能分别为0．497 1 eV／atom、0．484 2 eV／atom、0．497 5 eV／atom，明显偏小于“分散掺杂构型”，即“密集掺杂构型”不易获得，ZnBeO掺杂体系总是以“分散构型”出现．

2．3 ZnBeO掺杂体系的晶格参数和带隙

优化不同Be掺杂浓度下的ZnBeO结构，分散掺杂构型的晶格参数a（n）、c（n）和禁带宽度见图5．由于Be原子半径为0．14 nm，小于Zn原子的半径0．153 nm，导致随着掺杂浓度增加，晶格参数a（n）、c（n）均呈递减趋势．从图5可以看出，计算所得晶格参数呈线性变化，符合Vergard’s Law拟合带隙曲线．

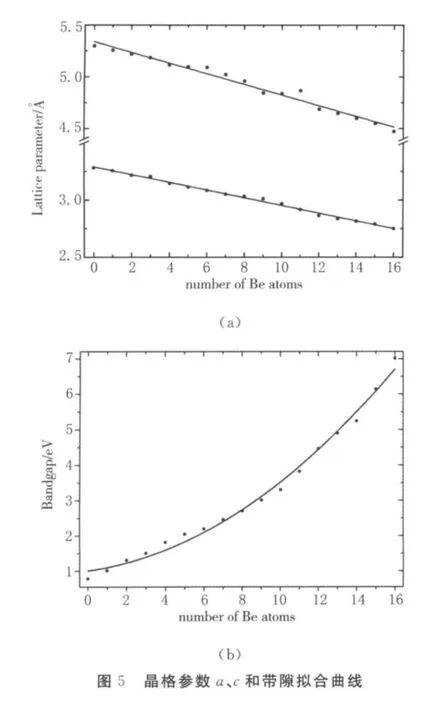
与Zn MgO掺杂体系相比，ZnBeO体系有望在很大程度上增大带隙，实现ZnO基器件在光电领域的突破．因此，禁带宽度Eg是ZnBeO掺杂体系的又一个重要参数．ZnBeO掺杂体系的带隙随Be浓度的变化公式为：Eg（x）＝x Eg，BeO＋（1－x）Eg，ZnO－bx（1－x）［21］．其 中，x＝n／16；Eg，BeO和Eg，ZnO分别是BeO和ZnO的禁带宽度；b是禁带弯曲系数，其大小表明体系的带隙相对于BeO和Zn O的偏离程度．图5（b）所示是带隙随Be浓度变化的拟合曲线，拟合用的带隙值为同一浓度下最稳构型的带隙值．计算得出ZnBeO的最稳定构型带隙值b为5．76 e V，这个结果与已有的理论计算结果相吻合［11，22］．

Be的掺入能极大增宽ZnBeO体系的带隙，主要是由于ZnBeO体系价带主要由O 2p和Zn 3d电子态组成，随着Be掺杂浓度的增加，Zn在体系中占的比重下降，导致价带向低能端移动，使得带隙增宽．

3 结 语

本文采用基于密度泛函理论的第一原理计算，详细计算了Be掺杂浓度为0～100%的Zn O的652种可能构型．通过比较不同构型的总能量，发现同一掺杂浓度下的不同构型中，掺入Zn O的Be原子不会出现聚集，总是处于分散状态，即Be原子掺杂总是以分散掺杂构型出现．这一结论与实验中观测到的ZnBeO体系无相分离一致．Be掺杂浓度为25%、50%、75%时，对应的Be原子数为4、8、12，此时掺入的Be原子均匀对称地分散在32个原子构成的超原胞中，此时的ZnBeO掺杂体系最稳定．通过对其几何结构进行优化，获得的晶格参数与实验值吻合较好，符合Vegard’s Law拟合带隙曲线．通过对掺杂体系的带隙的拟合，获得的禁带弯曲系数与已有结论吻合较好．利用Be掺入调制ZnBeO带隙，有望促进Zn O在光电领域的应用．

［1］ Kruefu V，Peterson E，Khantha C，et al．Flame－made Niobium Doped Zinc Oxide Nanoparticles in Bulk Heterojunction Solar Cells［J］．Applied Physics Letters，2010，97：053302－3．

［2］ Das S N，Moon K J，Kar J P，et al．ZnO Single Nanowire－based UV Detectors［J］．Applied Physics Letters，2010，97：022103－3．

［3］ Ohat H，Hosono H．Transparent Oxide Optoelectronics［J］．Materials Today，2004，7（6）：42－51．

［4］ Subramanyam T K，Mohan R G，Uthanna S．Process Parameter Dependent Property Studies on Cd O Films Prepared by DC Reactive Magnetron Sputtering［J］．Materials Chemistry and Physics，2001，69（1－3）：133－142．

［5］ Zhu Y Z，Chen G D，Ye H，et al．Electronic Structure and Phase Stability of MgO，ZnO，Cd O，and Related Ternary Alloys［J］．Physical Review B，2008，77：245209－7．

［6］ Das S，Chaudhuri S．Mg2＋Substitutions in ZnO－Al2O3Thin Films and Its Effect on the Optical Absorption Spectra of the Nanocomposite［J］．Applied Surface Science，2007，253（21）：8661－8668．

［7］ 唐鑫，吕海峰，马春雨，等．Be掺杂纤锌矿ZnO电子结构的第一原理研究［J］．物理学报，2008，57（12）：7806－7813．

［8］ Ohtomo A，Kawasaki M，Ohkubo I，et al．Structure and Optical Properties of ZnO／Mg0．2Zn0．8O Superlattices［J］．Applied Physics Letters，1999，75（7）：980－982．

［9］ 勒锡联，娄世云，孔德国，等．Mg掺杂ZnO所致的禁带宽度增大现象研究［J］．物理学报，2006，55（9）：4809－4815．

［10］ Khoshman J M，Ingram D C，Kordesch M E．Bandgap Engineering in Amorphous BexZnyO Thin Films［J］．Applied Physics Letters，2008，92：091902－3．

［11］ Ryu Y R，Lee T S，Lubguban J A，et al．Wide－band Gap Oxide Alloy：BeZnO［J］．Applied Physics Letters，2006，88：052103－3．

［12］ Ding S F，Fan G H，Li S T，et al．Theoretical Study of BexZn1－xO Alloys［J］．Physica B，2007，394（1）：127－131．

［13］ Zheng Y P，Chen Z G，Lu Y，et al．Influence of Be－doping on Electronic Structure and Optical Properties of ZnO［J］．Journal of Semiconductors，2008，29（12）：2316－2321．

［14］ 陈志雄，康炯．MgO光学性质的第一原理［J］．兰州大学学报（自然科学版），2011，47（1）：122－126．

［15］ Klingshirn C．ZnO：From Basics Towards Applications［J］．Physica Status Solidi B，2007，244（9）：3027－3073．

［16］ Hazen R M，Finger L W．High－pressure and High－temperature Crystal Chemistry of Beryllium Oxide［J］．Journal of Applied Physics，1986，59（11）：3728－3733．

［17］ Ching W Y，Xu Y N，Wong K W．Ground－state and Optical Properties of Cu2O and CuO Crystals［J］．Physical Review B，1998，40（11）：7684－7695．

［18］ Lu B，Zhou X，Linghu R F，et al．Be－composition Effect on Structure，Electronic and Optical Properties of BexZn1－xO Alloys［J］．Chinese Physics B，2011，20：036104－8．

［19］ Chang K J，Froyen S，Cohen M．The Electronic Band Structures for Zincblende and Wurtzite BeO ［J］．Journal of Physics C：Solid State Physics，1983，16（18）：3475－3480．

［20］ Paiva R De，Alves J L A，Nogueira R A，et al．Theoretical Study of the AlxGa1－xN Alloys［J］．Materials Science and Engineering B，2002，93（1－3）：2－5．

［21］ Cardona M．Optical Properties of the Silver and Cuprous Halides［J］．Physical Review，1963，129（1）：69－78．

［22］ Duan Y F，Shi H L，Qin L X．Elasticity，Band Structure，and Piezoelectricity of BexZn1－xO Alloys［J］．Physics Letters A，2008，372（16）：2930－2933．

The Effect of Be－composition on the ZnBeO Electronic Structure

ZHANG Niu1，LIU Ya－ming2，ZHANG Wen－qing2，HOU Zhen－yu2
（1．Zhongyuan University of Technology，Zhengzhou 450007；2．Henan Institute of Science and Technology，Xinxiang 453003，China）

Using first principle calculation based on density functional theory（DFT），the 652 different structures of the Zn16－nBenO16system are investigated．The results indicate that：the doped Be atoms in Zn O are homo－dispersed，don’t appear together．This coincides well with the experiment that one can’t find the phase separation between the Zn O and BeO．When doping density are 25%，50%and 75%，the doped Be atoms are distributed symmetrically in the 32－atom supercell，and the doping systems are in most steady state．As the Be composition varys from 0 to 100%，the calculated lattice parameters of the optimized doping structures are in good agreement with the experiments，and obey the Vegard’s Law well．Fitting the bandgap，the bowing coefficient b is about 5．76 e V．

Be doping；ZnO；first principle

O474

A

10．3969／j．issn．1671－6906．2012．03．007

1671－6906（2012）03－0034－05

2012－04－03

河南省基础与前沿技术研究计划项目（102300410128）；河南省教育厅科技攻关计划项目（2011B140008）

张 牛（1981－），男，河南郑州人，硕士．