乘法扰动下任意矩阵次酉极因子的扰动界
2012-10-25孔祥强
孔祥强
(菏泽学院 数学系,山东 菏泽274000)
乘法扰动下任意矩阵次酉极因子的扰动界
孔祥强
(菏泽学院 数学系,山东 菏泽274000)
利用矩阵的奇异值分解和广义极分解,在乘法扰动下,研究了任意矩阵次酉极因子的扰动界,得到了全新的扰动上界定理,所得结论将文献[3]中的列满秩矩阵推广到了非列满秩矩阵.
次酉极因子;广义极分解;扰动界
对矩阵次酉极因子扰动的研究是矩阵扰动问题研究的重要方向,国内外学者已对其进行了许多研究,并取得了很多成果.在文献[1]中给出了当A及其扰动矩阵均为列满秩矩阵时矩阵次酉极因子的扰动界;文献[2]研究了对于非满秩且有唯一广义极分解的矩阵,并进一步推广了文献[1]的结果;文献[3]中给出了任意酉不变范数下矩阵次酉极因子的扰动界.本文利用矩阵的奇异值分解和广义极分解,研究任意矩阵在乘法扰动下其次酉极因子的扰动上界,得到新的非满秩矩阵次酉极因子的扰动界,所得结果推广了文献[3]中的结论.
1 几个定义和定理
定义1[4]设A∈Cm×n,AHA的n个特征值的非负平方根为A的奇异值.若把AHA的特征值记作则A的奇异值为
定义2[4]如果1个定义在Cm×n上的非负实值函数‖·‖满足下列条件:为酉阵满足rank(A)=1,其中A,B∈Cm×n,则这个非负实值函数‖·‖称为Cm×n上的酉不变范数.
定义3[5]若Q∈Cm×n满足QHQ=I(n),则称Q为m×n酉矩阵;若Q∈Cm×n满足‖Q x‖2= ‖x‖2,∀x∈R(QH)((R(QH)表示由QH的所有列空间所张成的子空间),则称Q为m×n次酉矩阵.
设Q∈Crm×n,则Q为次酉矩阵的充分必要条件是Q=U1V1H,其中U1为m×r酉矩阵,V1为n×r酉矩阵[6].
定义4[5]若A∈Cm×n有分解A=QH,其中Q∈Cm×n为次酉矩阵,H∈Cn×n为半正定矩阵,则称该分解为A的广义极分解,称Q为次酉极因子.
定理1[4]设分块矩阵则对任一酉不变范数
定理2[4]设存在酉阵U及V,使得其中σr),σ1≥…≥σr>0,称此分解为矩阵A的奇异值分解.
定理3[4]设 ‖·‖ 为Cm×n上的酉不变范数,则有 ‖AB‖ ≤ ‖A‖2‖B‖,∀A∈Cm×m,∀B∈Cm×n和 ‖AB‖ ≤ ‖A‖‖B‖2,∀A∈Cm×n,∀B∈Cn×n.
定理4[6]设A∈Cm×n,则在条件R(QH)=R(H)限制下,A的广义极分解A=QH是唯一的,其中
2 主要结论
引理1[7]设M和N是2个Hermite(即MH=M,NH=N)矩阵,C是复矩阵且具有适当的维数,Δ=[α,β]⊂R,Δ′=R\(α-δ,β+δ),其中δ>0,如果λ(M)⊂Δ,λ(N)⊂Δ′,则矩阵方程MXXN=S存在唯一的解X,且对任意的酉不变范数‖·‖,有‖X‖≤‖S‖/δ.
引理2[3]设A当
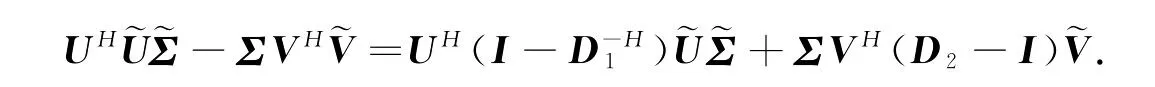
由矩阵的分块可得
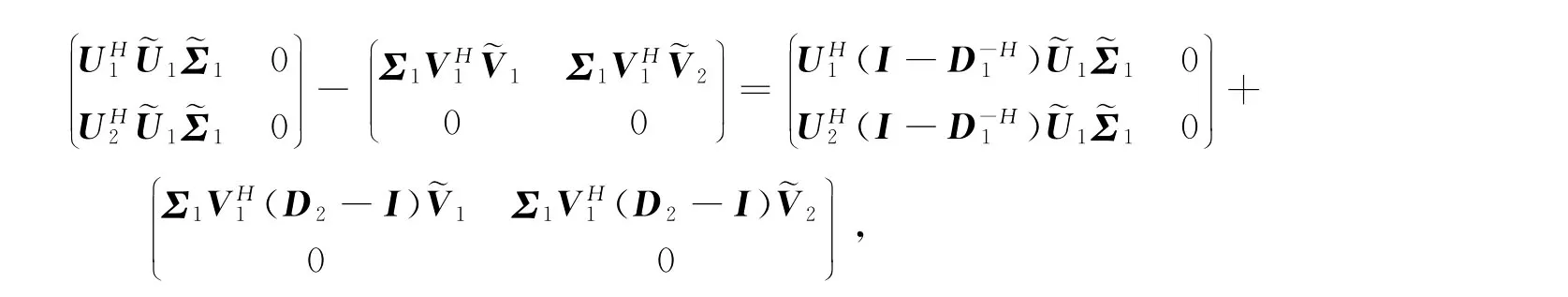
所以有
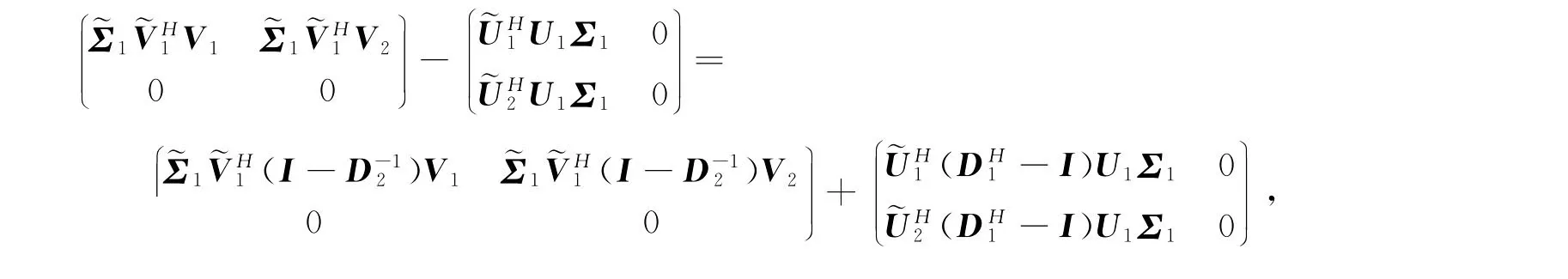
所以有
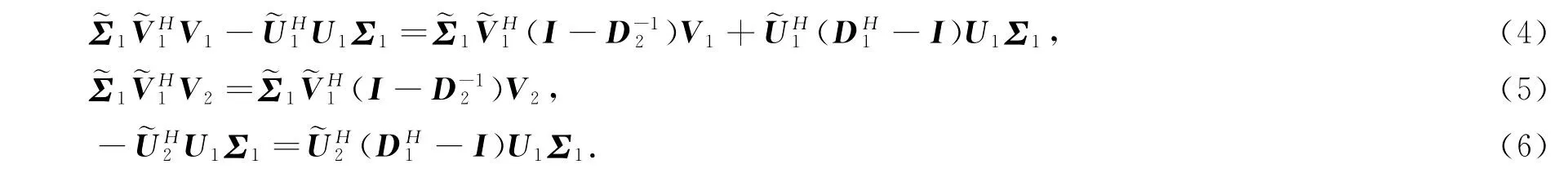
对(1)式进行共轭转置得

由(4)—(7)式得
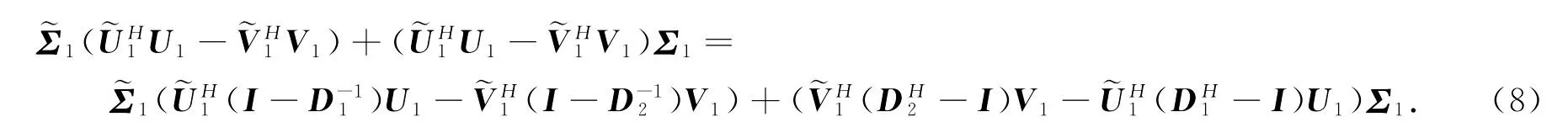
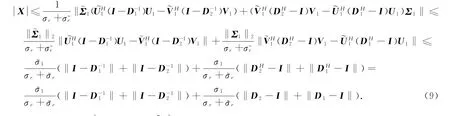

由Σ1和均为非奇异矩阵及(2)和(3)式可得


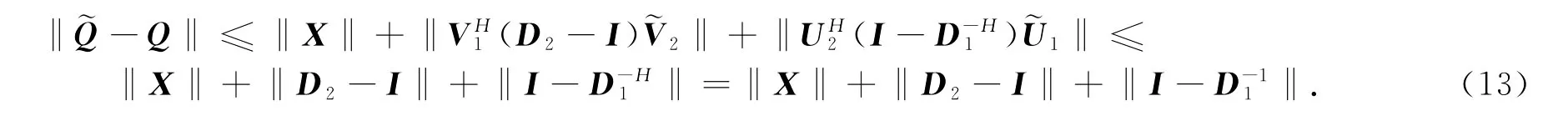

由Σ1和1均为非奇异矩阵及(5)和(6)式可得

由(14)—(16)式可得
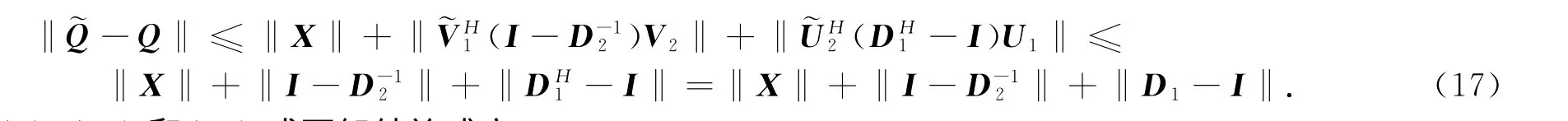
综合(9)、(13)和(17)式可知结论成立.
[1] Li R C.Relative perturbation bounds for the unitary polar factor[J].BIT,1997,37(1):67-75.
[2] Chen X S,Li W,Sun W W.Some new perturbation bounds for the generalized polar decomposition[J].BIT,2004,44(2):237-244.
[3] 陈小山,黎稳.酉不变范数下极分解的扰动界[J].计算数学,2005,27(2):121-128.
[4] 孙继广.矩阵扰动分析[M].2版.北京:科学出版社,2001:12-49.
[5] 孙继广,陈春晖.广义极分解[J].计算数学,1989,11(3):262-273.
[6] Ben-Israel A,Greville T.Generalized inverses:theory and applications[M].New York:Springer-Verlag,2003:218-220.
[7] Bhatia R.Matrix analysis[M].New York:Springer,1997:152-157.
Multiplicative perturbation bounds of the sub-unitary polar factor for arbitrary matrices
KONG Xiang-qiang
(Department of Mathematics,Heze University,Heze 274000,China)
Using the singular value decomposition and generalized polar decomposition,the multiplicative perturbation bounds of the sub-unitary polar factor for arbitrary matrices are studied.Some new perturbation bounds are presented,the results extend the full column rank matrix of original conclusions to the non-full column rank matrix.
sub-unitary polar factor;generalized polar decomposition;perturbation bound
O241.6
A
1004-4353(2012)03-0196-04
20120302 作者简介:孔祥强(1983—),男,助教,研究方向为应用数学.
山东省统计局重点课题项目(KT11048);山东省教育科学“十二五”规划重点课题项目(2011GG049)
