椭圆台型腔加工固定循环功能的实现*

2012-10-24胡翔云

制造技术与机床 2012年11期

胡翔云

（湖北职业技术学院，湖北孝感 432000）

市场上的数控系统没有椭圆型腔和圆台形型腔加工固定循环功能，一般也没有椭圆插补功能。在加工这类型腔时，如采用计算机自动编程，程序很长，修改也不方便［1］。这里通过建立该类特征加工的数学模型，利用数控系统提供的用户宏程序功能编制宏程序，然后设置成椭圆型腔加工固定循环功能，对数控系统的功能进行扩展。

1 加工工艺分析

在实际生产中出现的椭圆型腔（顶部和底部均为椭圆）、圆变椭圆型腔（顶部和底部一个为椭圆形，另一个为圆形）、甚至圆台形型腔和椭圆台型腔，都可归为椭圆型腔一类进行研究。这是因为圆可认为是长轴与短轴尺寸相等的椭圆。为分析方便起见，将椭圆型腔从零件中抽出单独研究（见图1）。椭圆型腔的加工可认为是加工椭圆台的“内壁”。

如图1所示，椭圆台可看成是直线MN上的两点M、N分别沿着顶部椭圆O1、底部椭圆O2的轮廓线以等角速度旋转所形成的面合围而成。可以证明，如果用一张平行于水平面的平面去截椭圆台，所得交线仍为椭圆。对于这类零件的加工，一般采用等高线法［2］。其基本原理是将椭圆台从上到下分成若干与水平面平行的薄片，薄片与椭圆台的交线为一条等高线，一次切削一层等高线，切完一层再切第二层，直到切完整个椭圆台内表面为止［3］。在采用等高线法切削的过程中，刀具的刀位点Z向高度不变，称为刀心等高法。

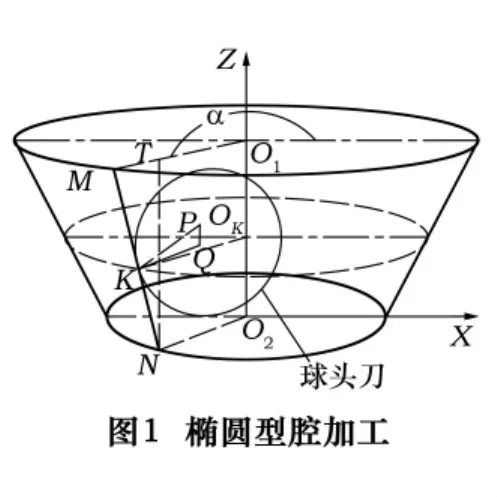
采用刀心等高法时，只能用平底立铣刀切削。立铣刀的刀位点在刀具底部中心，铣削K点所在的椭圆轮廓时，刀具下刀到K点位置，刀心始终偏移虚线椭圆轮廓线一个刀具半径即可完成该高度处椭圆的切削，编程比较简单。但是立铣刀切削曲面时，切成的曲面成阶梯状，表面粗糙度值很大，为减小粗糙度值，只有缩小步距，此时主要依靠立铣刀最底部处的一小段侧刃切削，导致此处切削刃极易磨损，进一步增大加工误差，且程序循环次数大增，切削效率低下。因而切削斜面时，立铣刀只用于开粗，半精加工和精加工均不采用立铣刀。切削斜面最为有效的刀具是球刀、牛鼻刀、鼓形刀，以球刀最为常用［4］。使用球刀切削时，如果仍采用刀心等高法，由于椭圆台四周的斜度是不同的，则一定会在较为平缓的地方产生过切（如图2a所示）。要使球刀面在某一等高线处与凸台面始终保持相切，则球刀的刀心X、Y、Z坐标都应作相应变化（如图2b所示）。即应采用刀心变高切削等高线的方法（简称刀心变高法）。

切削椭圆时，虽然一般的数控系统没有椭圆插补功能，但可用小直线段去逼近椭圆轮廓线，直线逼近椭圆弧的节点坐标可以利用循环语句让数控系统自动计算［5］。

2 数值计算

2．1 计算点K所在椭圆的长半轴和短半轴

设椭圆台底部椭圆长半轴为a，短半轴为b，椭圆台顶部椭圆长半轴为c，短半轴为d，凸台高为h，刀具半径为r。由于椭圆台形状的特殊性，编写宏程序时要引入两个循环变量，一个是K点至底面的高度变量i，一个是椭圆上任意一点K与椭圆对称中心OK的连线与X轴的夹角α，点K所处椭圆的长半轴、短半轴用e、f表示。利用初等几何知识不难得到:

即，凸台上任意高度处的椭圆长半轴e、短半轴f的尺寸可由高度循环变量i表示。

2．2 计算刀心坐标

要保证球刀与椭圆台壁切点的轨迹是一条等高线，球刀刀心坐标必随切削等高线时位置不同而变化。根据椭圆参数方程，利用几何和导数知识可以计算出刀心P的坐标（这里略去计算过程）。

式中:h为椭圆型腔深度;i为为高度变量;e、f为分别为高度i处椭圆的长半轴、短半轴;r为刀头半径;α为椭圆转角。

由此可见，xP、yP、zP可由高度循环变量i及椭圆转角变量α表示。由于模型中有两个变量，所以编程时需要两次循环。

上面的分析中，当顶部或底部中的一个或全部为圆时，各式仍然成立。故该数学模型不仅适用于椭圆型腔，也适用于圆变椭圆型腔和圆台形型腔，也适用于椭圆柱型腔或圆柱型腔。

3 误差预测方法

3．1 预测加工方法误差δ1

在一定的下刀步距k下，球刀在斜面较为平缓处加工误差最大。而较为平缓处要么为长轴处，要么为短轴处（对于实际零件，很容易区分），假设在长轴处最平缓，则由图3可知:

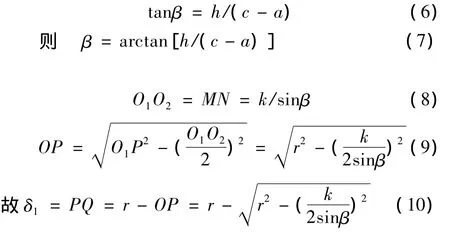
式（7）、（10）即为加工方法误差δ1预测计算公式。

3．2 预测逼近误差δ2

该方法采用小直线段逼近椭圆和圆（刀心以小直线段运动、实际切削点轨迹为近似直线段），存在着逼近误差。显然，在曲率半径最小处误差δ2最大。曲率半径最小处要么为顶部椭圆长轴处，要么为底部椭圆长轴处。因此只需要判断这两个地方的逼近误差。

以凸台任一高度处的椭圆作为研究对象。在图4中，作步距角θ，并作其角平分线O2M，交椭圆于M，交CD于N（后面的编程中，椭圆转角是从0到2π变化的，故C、D是在水平线的同一侧，而不是对称于水平线）。逼近误差δ2应为线段CD与椭圆弧CD之间的最大距离。为简化计算，这里用MN之长近似代替逼近误差δ2。

由椭圆的性质知，在XY平面内，C点坐标为（e，0），D点坐标为（ecosθ，fsinθ），M点坐标为（ecos（θ/2），fsin（θ/2））。由于 θ角很小，点N近似为CD中点，则N点坐标为

根据式（13），用顶部和底部椭圆的长半轴和短半轴尺寸分别替换公式中的e、f，求得δ2（取较大值）。

4 固定循环功能的实现

4．1 编写宏程序

这里基于FANUC Series 0i－MODEL D数控系统编写宏程序，以椭圆台底面中心为工件原点（见图1）。宏程序编制如下:

将该宏开发为一个固定循环的方法是，事先在数控系统的参数中设定一个G代码号（这里设定为G93，宏程序名取为O9018），由于FUNAC系统中宏程序名O9018对应的参数号为6058，故通过设定参数（No．6058）=93，即将上述宏程序命名为G93椭圆型腔加工固定循环功能［6］。这里使用第一类自变量指定法，其格式是:

G93A_B_C_I_J_R_S_T_L_;

式中:A、B、C、I、J、R、S、T、L 分别为底部椭圆长半轴、短半轴、顶部椭圆长半轴、短半轴、型腔深度、球刀半径、下刀步距、角步距、调用循环次数。

将该宏程序存放在数控系统中，当有类似加工特征出现时，只需通过加工程序调用这个宏程序，并给相关变量赋值就能完成工件加工，相当于给数控系统增加了一个固定循环功能。