精纺毛织物最大缝缩率与面料的纱向角度相关性模型的讨论

刘冠彬，王玉岭，张文斌

（1.厦门理工学院 设计艺术系，福建 厦门 361024；2.东华大学 服装和艺术设计学院，上海 200051）

精纺毛织物最大缝缩率与面料的纱向角度相关性模型的讨论

刘冠彬1，2，王玉岭2，张文斌2

（1.厦门理工学院 设计艺术系，福建 厦门 361024；2.东华大学 服装和艺术设计学院，上海 200051）

在精纺毛织物缝合工艺体系中，缝边的不同纱向角度对缝合的最大缝缩率的影响是结构和工艺立体配伍的基础.为构建最大缝缩率的理论方程，从力学平衡角度探讨面料力学性能对缝缩率的影响，分析不同纱向角度的面料之间缝合最大缝缩率的关系.研究表明，在纱向角度为0°～45°时，面料的最大缝缩率随纱向角度的增大而增大；在纱向角度为45°～90°时，面料的最大缝缩率随纱向角度的增大而减小.试验验证结果表明，本文提出的轻薄精纺毛织物不同纱向角度面料最大缝缩率理论模型具有一定的实用操作性.

精纺毛织物；最大缝缩率；纱向角度；面料力学性能

基于服装工艺技术角度，面料缝合成型性的研究在近10年已成为关注的热点，但是基于结构工艺立体配伍角度的研究并不多.关于探讨最大缝缩率和面料物理力学性能关系的研究已有相关报道.MASAKO［1］探讨了新合纤织物缝缩率与力学性能的关系，并得到了不同服装面料缝纫起皱的预测方程.YANADA［2］从实用性出发探讨了缝纫起皱等级与织物力学性能的关系，导出了男西装与女装服用面料的回归方程，用于对面料缝制品质的预测及选择，并建立相关模型.杨建忠等［3］根据弹性体的屈曲变形理论，对轻薄织物屈曲变形作了理论分析，计算了轻薄织物水平方向屈曲最短理论长度，分析了轻薄织物屈曲最短理论长度与实测缝纫厚度应变和AATCC评级相关性.在羊毛面料超喂缝缩率与力学性能的关系中，许同洪等［4］以FAST测试仪测得相关数据来预测毛面料超喂缝制下的缝缩率，建立了面料超喂缝纫时缝缩率与织物弯拉模量比之间的理论方程.但这些研究并没有从面料的几何形状的缝合关系来讨论不同面料、不同纱向角度等关键因素之间的相关性，分析其对缝合工艺的影响，也没有深入到建立工艺配伍模型的缝合规则，来指导服装造型结构工艺的设计.

1 精纺毛织物最大缝缩率的理论模型

图1所示为面料A及B缝合力学平衡分析图，其中，lA为缝合时较长面料的长度；lB为缝合时较短面料的长度.

图1 试样A和B缝合力学平衡分析图Fig.1 The analysis figure on the mechanics balance of sewing between sample Aand B

f1＋f2＝0，得

故M（x）＝－f（x）y，

又f（x）＝kΔx ＝k（x－lB），得到f（l0）＝k（l0－lB），则

其中：EI为面料的弯曲模量；k为面料的拉伸弹性系数；l0为最大缝缩时稳定的长度；n表示缝合单元数；x为面料缝缩横向的改变量.

2 纱向角度对面料缝缩率影响的相关因子分析

由于面料具有各向异性，因此，面料的纱向角度对面料的力学性能有较大的影响，由式（1）可知，值基本上决定了织物的最大缝缩率时平衡量l0，所以讨论面料纱向角度对值的影响具有较高的现实意义.

服装制作过程中，结构线的缝合很少沿经向或纬向缝合，大部分是不同角度纱线间的缝合，因此，不同角度纱线间缝合的缝缩率对服装造型影响的研究相当重要.

2.1 纱向角度与B值的关系

由文献［5］有式（2）和（3）.

其中：BFAST（θ）为用FAST测试得到的弯曲刚度；BKES（θ）为用KES测试得到的弯曲刚度；B（θ）B为面料弯曲后形成圆柱面时平行于圆柱面轴线的弯曲刚度；B（θ）T为垂直于圆柱面的弯曲刚度；θ为纱向角度；B（90°）和B（0°）分别为面料经向和纬向弯曲刚度；J（90°）和J（0°）分别为经向纱线和纬向纱线在斜向弯曲时呈现的抗扭刚度.

通常情况下，B（θ）T随面料斜向变化程度较小，因此，需测量的面料弯曲刚度主要是平行于圆柱面轴线的B （θ）B.

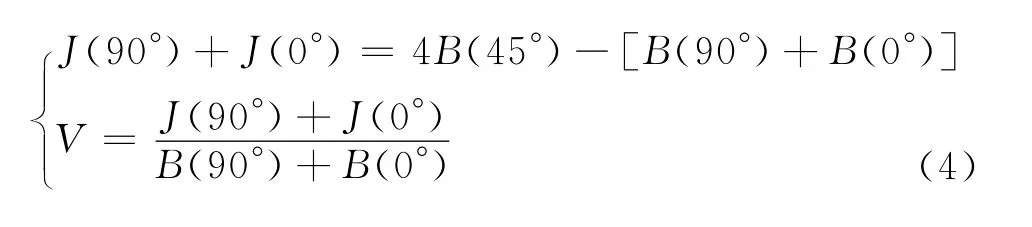
由式（3）和（4）可知，当V ＝0时，J（90°）和J（0°）可忽略，面料在经、纬向之间的斜向弯曲刚度会出现明显最小值，此时

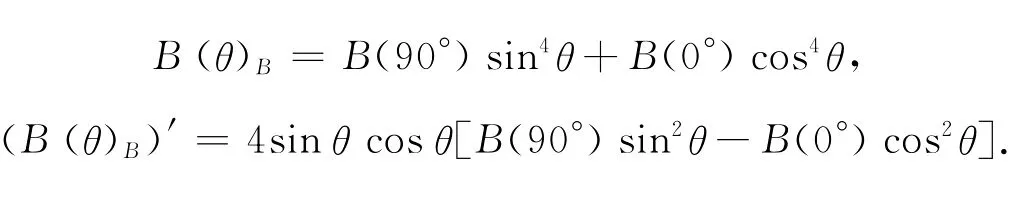
当V ＝ 1 时，J（90°）＝ B（90°），J（0°）＝B（0°），面料的弯曲刚度除在0°和90°时没有最小值，此时

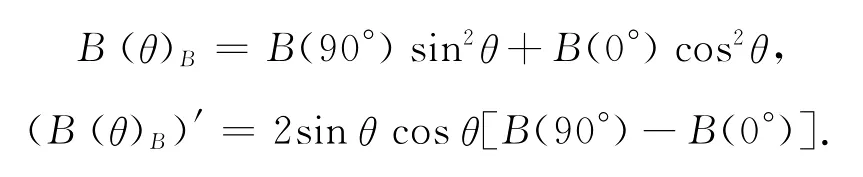
在0°≤θ≤90°范围内，B（θ）值单调递增.

当0＜V ＜1时，令4B（45°）－ ［B（90°）＋B（0°）］＝ M，则

在0°≤θ≤45°时，cosθ＞sinθ；在45°≤θ≤90°时，cosθ＜sinθ.通过对14种面料经纬向和斜45°的B值测量可知：2B（90°）－M＞0；M－2B（0°）＜0且｜2B（90°）－M｜＞｜M－2B（0°）｜.因此，B（θ）在45°≤θ≤90°时单调递增，在0°≤θ≤45°范围内，只有当sin2θ［2B（90°）－M］＋cos2θ［M－2B（0°）］≥0时，θ≥arctan，即B（θ）在0°≤θ≤arctan时单调递减，在

2.2 纱向角度与k值的关系

由于织物的弹性系数k与织物小负荷下的弹性模量E的10倍在数值上近似相等，因此，本文采用面料在定负荷（4.9和19.6cN/cm）下的弹性模量，计算弹性系数k值.由文献［6］有式（5）.其中：E（θ）为定负荷下面料沿与纬向θ角度下的弹性模量；E（90°）和E（0°）分别为定负荷下面料沿经、纬向下的弹性模量；G为面料在平面内的剪切模量；ν12为泊松比.

对于宽5cm、长30cm的试样面料，在定负荷下，其45°斜向的弹性模量可由INSTRON织物强力测试仪测得.

对面料 （FA，［λX·λY－θ1］）和 （FB，［λX·λ1Y－θ2］）之间进行吃势的缝合，其中：λX，λY和θ分别为面料A和B的缝合长度和宽度及面料的纱向角度.最大缝缩率sUA＝×100%.

由式（2）知，EI值与B 值呈正比，在0°≤θ≤90°范围内，EI值与B值同步变化，且EI值随θ值的增大而呈现出先递减再递增的趋势.由于k在小负荷力作用下与10 E值近似相等，因此k值的变化与E值同步，即在0°≤θ≤90°范围内，k值随θ值的增大呈现先递减再递增的趋势.综上所述，由≥0可知：0°≤θ≤45°时，随θ值的增大而递减，最大缩缝率sUA随θ值的增大而递增；45°＜θ≤90°范围附近，（θ）随θ值的增大而递增，sUA随θ值的增大而递减.

2.4 不同纱向角度的面料之间缝合的缝缩率分析

λ1Y≥λY且θ1≠θ2，由缝缩平衡方程l0＝π·可知，得到缝缩后平衡点时，其中 （FB，［λX·－θ2］）决 定 EI 值大 小，（FA，［λX·λY－θ1］）决定k值，即由于面料的各向异性，不同纱向使值产生比较大的变化，被吃势的面料（较长的面料）决定EI值，吃势的面料（较短的面料）决定k值.

在0°≤θ≤45°时，不同纱向角度面料间的缩缝采取缩缝较大角度的试样，因此，对于被吃势的面料，其角度固定后，EI值为定值；随着吃势的面料纱向角度的增加，其k值逐渐增大，被吃势的面料和吃势的面料经缩缝组合后，组合体的随吃势的面料纱向角度的增大而减小，被吃势面料的缩缝率随之增大.在45°＜θ≤90°时，不同纱向角度面料的缩缝采取缩缝较小角度的试样，因此对于被吃势的面料，其纱向角度固定后，EI值为定值；随着吃势的面料纱向角度的增加，其k值逐渐减小，被吃势的面料和吃势的面料经缩缝组合后，组合体的随

吃势的面料纱向角度的增加而增大，被吃势的面料的缩缝率随之减小.

3 试验验证

为检验同种轻薄精纺毛织物的不同纱向角度的面料缝缩率关系，本文从14种试验面料选取4种具有不同结构规格参数的面料，以验证不同纱线角度面料缝缩率的理论值与实测值的关系.

3.1 试验

试样面料在0°，45°和90°（如图2（a）所示）的B（θ）和E（θ）值分别由 KES－FB系统和INSTRON织物强力仪（如图2（b）所示）测得，结果如表1所示.

图2 INSTRON织物强力仪及试样图Fig.2 Fabric tensile strength instrument and sample

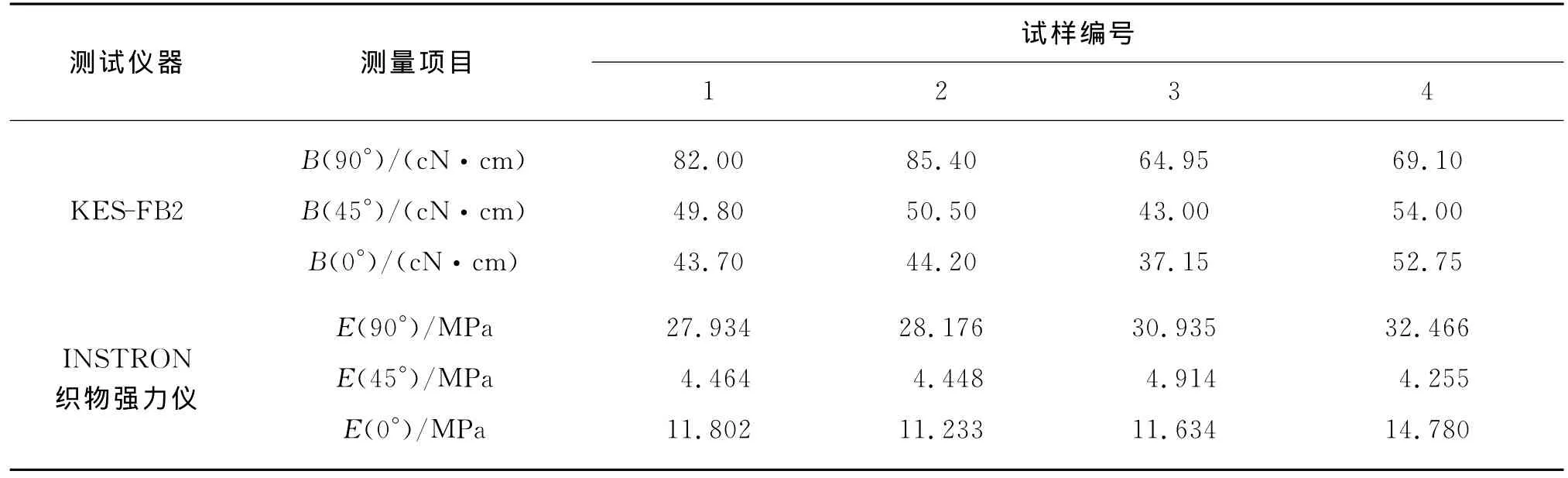
表1 织物理论缝缩率测量值Table 1 Sewing shrinkage values of fabric in theory

3.2 B和k值的计算

由式（3）和（5）可得4种试验面料不同角度下的B和k值如图3和4所示.由图3和4可知，轻薄精纺毛织物的弯曲刚度在0°～90°范围内呈现先减小再增大的趋势，与前面理论分析结果基本一致；其拉伸弹性系数在0°～90°范围内呈现先减小再增大的趋势，试验结果与前面理论分析结果一致.

图3 4种不同精纺毛织物的纱向角度与织物弯曲刚度的变化关系图Fig.3 The relationship between yarn angle and fabric bending ligidity of four different worsted fabrics

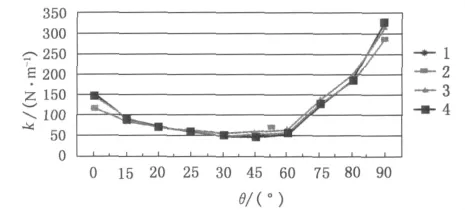
图4 4种不同精纺毛织物的纱向角度与织物拉伸弹性系数的变化关系图Fig.4 The relationship between yarn angle and fabric tensile elastic coefficient of four different worsted fabrics

3.3 理论值与实测值的关系

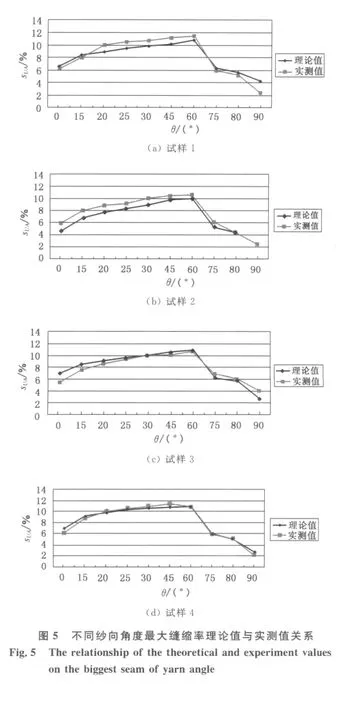
4种试样的不同纱向角度缝合时的最大缝缩率理论值与实测值比较关系如图5所示.由图5可以看出，试样的理论值与实测值趋于一致，说明轻薄精纺毛织物不同纱向角度面料最大缝缩率的理论方程具有一定的实用操作性.由于本文主要研究面料力学性能对缝缩率的影响，没有考虑缝线张力对面料缝合的影响，因此，缝缩率的理论计算值与实测值之间有一定的误差，应用时应考虑缝线的张力给予修正.

4 结 语

根据缝合最大缝缩率的理论方程，对影响缝缩率的面料纱向角度进行分析和试验验证，得到如下结论.

（1）在0°≤θ≤45°时，不同纱向角度面料间的缩缝采取缩缝较大纱向角度的试样，因此，在被吃势的面料纱向角度固定后，其EI值为定值；随着吃势的面料纱向角度的增加，其k值逐渐增大，被吃势的面料和吃势的面料经缩缝组合后，组合体的随吃势的面料纱向角度的增大而减小，被吃势的面料的缩缝率随之增大.

（2）在45°＜θ≤90°时，不同纱向角度面料的缩缝采取缩缝较小纱向角度的试样，因此，在被吃势的面料纱向角度固定后，其EI值为定值；随着吃势的面料纱向角度的增加，其k值逐渐减小，被吃势的面料和吃势的面料经缩缝组合后，组合体的随吃势的面料纱向角度的增加而增大，被吃势的面料的缩缝率随之减小.

［1］MASAKO N.Sewability of new synthetic fabric［J］.Jpn Res Assn Text End－Uses，1994，35（1）：20－－29.

［2］YANADA Y.A study on seam pucking［J］.Jpn Res Assn Text End－Uses，1993，34（3）：37－45.

［3］杨建忠，王善元.轻薄织物屈曲变形与缝纫起皱关系的研究［J］.西北纺织工学院学报，2001，15（1）：5－10.

［4］许同洪，顾平.羊毛面料的超喂缝缩率与力学性能的关系［J］.纺织学报，2009，30（7）：47－50.

［5］COOPER D N E.The effect of twist upon bending properties［J］.Textile Research Journal，1960，30：150－151.doi：10.1177/004051756003000207.

［6］COOPER D N E.The stiffness of woven textile［J］.Journal of the Textile Institute Transactions，1960，51（8）：317－335.

The Discussion of the Relativity Model of Maximum Sew Shrinkage by Sewing Worsted Fabric and the Fabric's Yarn Angle

LIU Guan－bin1，2，WANG Yu－ling2，ZHANG Wen－bin2
（1.Faculty of Design Arts，Xiamen University of Technology，Fujian Xiamen 361024，China；2.Fashion and Art Design Institute，Donghua University，Shanghai 200051，China）

In the worsted fabrics suture technical system，different seam yarn angles lead to different maximum sew shrinkage，which is the foundation of the compatibility between structure and technician.In order to get the theory equation of the maximum sew shrinkage，the effects of the fabric mechanical properties to the maximum sew shrinkage are discussed based on the mechanical balance.The effects of the yarn angles to the maximum sew shrinkage are also analyzed.The research result indicates that while the yarn angle is 0°－4 5°，the maximum sew shrinkage of fabric is increased with the increase of yarn angle，but decreased while the yarn angle is 4 5°－9 0°.The experiment verifies that the proposed worsted fabric with different yarn angle of maximum sew shrinkage theoretical model has certain practical operation.

worsted fabrics；maximum sew shrinkage；yarn angle；fabric mechanical properties

TS 941.63

A

2011－04－14

刘冠彬（1971—），男，湖南邵东人，副教授，博士，研究方向为数字化服装技术和高级服装设计.E－mail：liuguanbingfd＠163.com

1671－0444（2012）03－0303－05