碳纤维长丝屈曲排布对电磁波屏蔽性能的影响

吴 瑜，周 胜，徐增波，于伟东

（1.东华大学 纺织学院，上海 201620；2.扬州职业大学 纺织服装系，江苏 扬州 225012；3.上海工程技术大学 服装学院，上海 201620）

碳纤维长丝屈曲排布对电磁波屏蔽性能的影响

吴 瑜1，周 胜2，徐增波3，于伟东1

（1.东华大学 纺织学院，上海 201620；2.扬州职业大学 纺织服装系，江苏 扬州 225012；3.上海工程技术大学 服装学院，上海 201620）

基于所提出的屈曲排布模型制作了碳纤维屏蔽材料，探讨了辐射源频率、屈曲波幅和行间距对其在微波段电磁波（EMW）屏蔽性能的影响.结果表明，辐射源频率因素影响显著，且屈曲排布碳纤维屏蔽材料在1.4～2.0GHz频段内具有良好的屏蔽效果；屈曲波幅和行间距对屏蔽性能影响显著，屈曲波幅为2 H（H为厚度）和行间距为5mm的试样，在测试范围内屏蔽效果相对最优；碳纤维含量的增加对屏蔽性能的影响并不显著.

碳纤维长丝；屈曲排布；电磁波；屏蔽性能；有效屏蔽能

电器、通讯等电子产品及侦测装备是电磁辐射源，易对环境造成电磁污染［1－2］.电磁污染不仅干扰电气电子设备的正常运行，而且严重危害人体健康，人体和电子设备都需要防护［3－4］.对人体的防护，尤其是以织物为对象所进行的屏蔽性能的改进已有众多报道，但大多为材料组成方式及其配比的选择［5－6］.碳 纤 维［7－8］和 碳 纳 米 材 料［9－10］作 为 组 分 掺 入的复合材料的屏蔽性能已有讨论，但有关碳纤维屈曲排布状态对电磁波的屏蔽性能的研究鲜见报道.本文采用未经任何处理的碳纤维长丝的屈曲排布，讨论屈曲排布对屏蔽性能的影响，并通过试验验证屈曲排布效果，以求得到碳纤维长丝束屈曲排布应用的基本数据.

1 试样制备及性能测试

1.1 试验材料

试验所用的碳纤维是由南通森友碳纤维有限公司生产的聚丙烯腈（PAN）基碳纤维长丝束，其线密度为200tex/3 000f，密度为1.44g/cm3，线电阻为1.57 Ω/cm，电阻率为4.4×10－2Ω·m，单丝直径为7～8μm.

试验所用结构支撑材料是对电磁波无任何影响的发泡聚苯乙烯材料［11］，即PS发泡片，尺寸为30cm×30cm，厚度H 为1.66mm.碳纤维长丝束以屈曲波的形式沿PS发泡片平面方向逐束等间距地穿入其中.通过调节碳纤维丝束间的距离即行间距d来调节单位体积内碳纤维的含量，并同步改变上下起伏的长度即针距λ来改变屈曲波的形态，通过调节PS发泡片的层数n来调节试样的厚度t和碳纤维长丝束的屈曲波波幅h.图1所示为n＝2时试样的三维效果图，层与层之间自然贴近无间隙.显然：

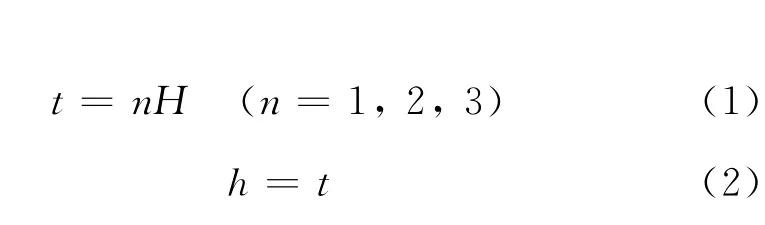
采取行间距d与针距λ一半相等的变化方式，即

由此双向同时增加碳纤维的含量.各试样编号及结构参数如表1所示.

图1 试样结构三维效果图Fig.1 3D drawing of sample structure

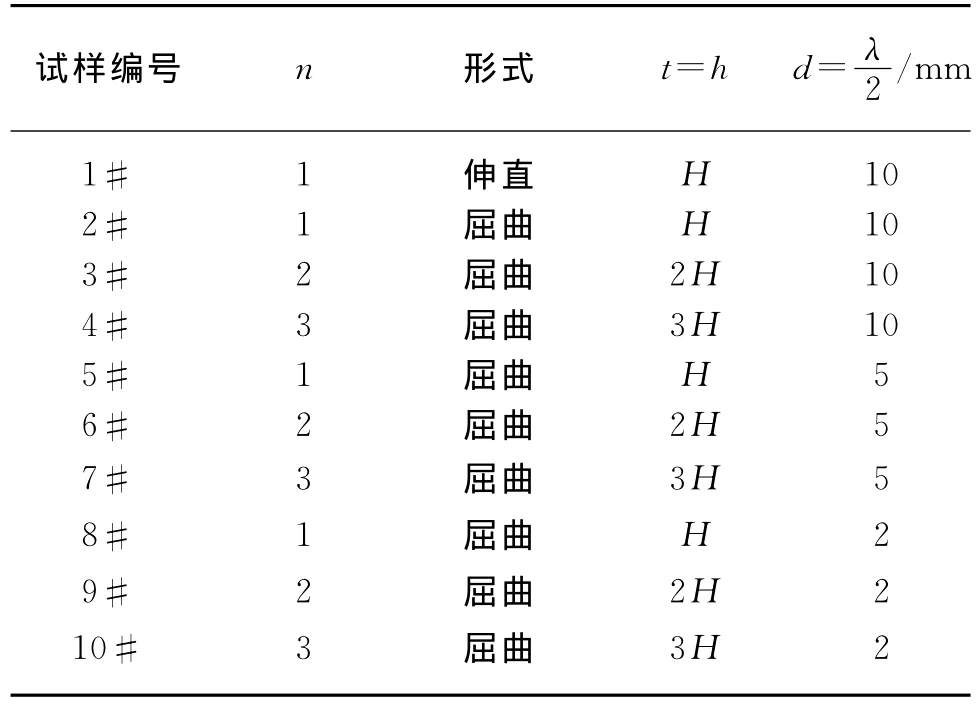
表1 试样编号及结构参数Table 1 Samples specifications

1.2 测试仪器及方法

（1）测试仪器.仪器设备主要由电磁波信号发生器、测量台和频谱分析仪组成，其连接配置如图2所示.电磁波信号发生器为安立MG 3642A型，其频率范围为125kHz～2.08GHz；特性阻抗为50 Ω；分辨率为0.01Hz和0.01dB；测量的动态范围＞100dB，作为电磁波信号源.

（2）测试方法.采用图2所示的装置进行测试，采取扫频方式，测量范围为0.05～2.00GHz，扫描间隔带宽为0.01GHz，计算的指标为屏蔽效能［12］（shielding efficiency，SE）.计算方法如式（4）所示.

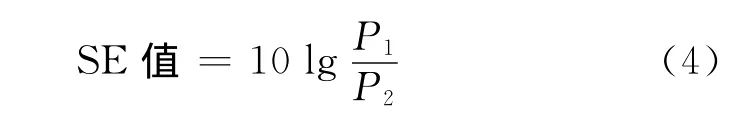
式中：P1为测试台中空程时的接收功率；P2为测试台中负载试样时的接收功率.

2 试验结果与分析

2.1 排布方式对屏蔽性能的影响

碳纤维长丝束分别以伸直和屈曲两种形式以10mm为行间距排布在厚度为H的PS发泡片上，即屈曲排布的屈曲波幅为H，见表1中的1＃和2＃试样.其对电磁波屏蔽效能（electromagnetic shielding efficiency，EMSE）测量结果如图3所示.

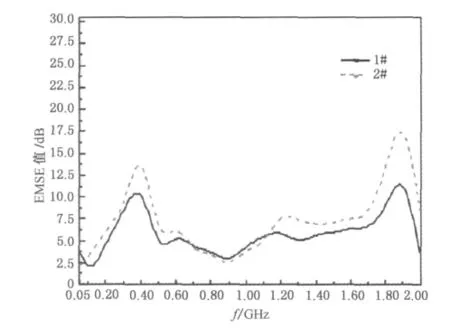
图3 不同排列方式对电磁波屏蔽效能的影响Fig.3 Effect of different arrangement on EMSE

由图3可知，2＃试样即碳纤维长丝束屈曲排布时，电磁波屏蔽效能明显高于伸直排布的1＃试样，且两者的屏蔽曲线形状大致相同.这说明二者对电磁波的衰减原理有一致之处，只是伸直碳纤维束在PS发泡片中的含量相对较少；伸直排布时碳纤维与电磁波传递方向正交，故相对路径较短，而屈曲排布中由于碳纤维的倾斜使电磁波穿过纤维的路径（即厚度）增加；屈曲排布增加了纤维的含量，即入射切面的椭圆化.

另外，在高频电磁场中，电磁波在导线表面产生涡流，电流分布将呈现向导体表面集中的现象，即所谓的趋肤效应［13］.由于碳纤维长丝束很细，较大的表面积会产生涡流损耗，从而导致电磁波能量的衰减.屈曲的纤维因长度的增加而使表面积增加，故使趋肤效应增加，材料的屏蔽性能提高.

此外，碳纤维还会产生特定的散射，发生类似相位对消现象［14］引起的电磁波损耗，这是因为碳纤维长丝束屈曲排布时，入射电磁波亦会在屈曲的碳纤维片段上产生较多的漫散射，从而减少了在特定方向上电磁波的强度.

因此，碳纤维质量增加、穿过路径增加、趋肤效应增强和对消散射增强，使2＃试样因屈曲排布呈现出的电磁波屏蔽性能明显优于1＃试样.

2.2 屈曲波幅对屏蔽性能的影响

当碳纤维长丝束排布的行间距d和其屈曲半波长λ/2相等且取定值，测量不同屈曲波幅试样的屏蔽谱，结果如图4所示.由图4可知，行间距一定时，在相同辐射频率的情况下，不同屈曲波幅试样的屏蔽效能不同.在d＝λ/2为某定值时，屈曲波幅h的增大意味着碳纤维质量或填充比例在增加，试样屏蔽效能曲线应该呈现如图3中低频段（0.2～0.8GHz）和高频段（1.4 ～2.0GHz）的趋势，因而h值越大，屏蔽曲线应该是整体上移.但在3种定行间距的条件下，未呈现这一规律，只是在本文测量的低频段和高频段有变化，但增减规律不明显.

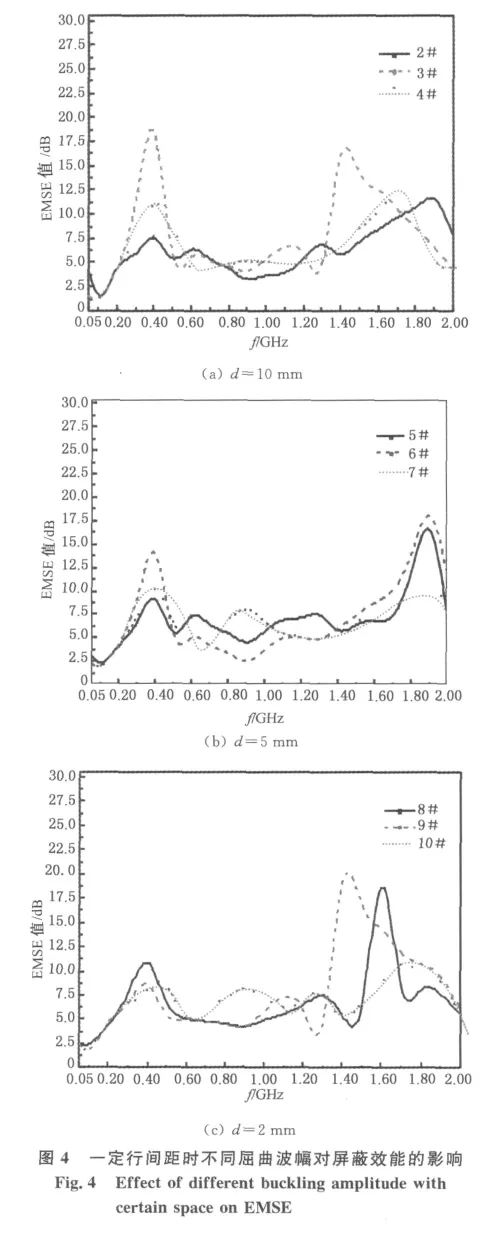
由图4可知，（1）各曲线均有特征峰，只是峰值不同，相对而言，除d＝2mm外，h值大的试样，其特征峰值亦大，且h＝2 H 时最大；（2）在中频段（0.8～1.4GHz）都显示出较低的屏蔽性能；（3）在高频段，当d＝5mm时，对应的3种屈曲波幅有相同位置的峰外，其他都有特征峰偏移的现象；（4）相对而言，屈曲波幅为2 H时的屏蔽性能在整体上最大，即屏蔽效果最好；（5）整体而言，屈曲波幅h增大，碳纤维质量和吸收厚度增加，电磁波入射角和屈曲纤维表面的夹角增大，散射加强，在双重反向作用下屏蔽性能有2 H＞H＞3 H的趋势，即有极值.

2.3 纤维束行间距对屏蔽性能的影响

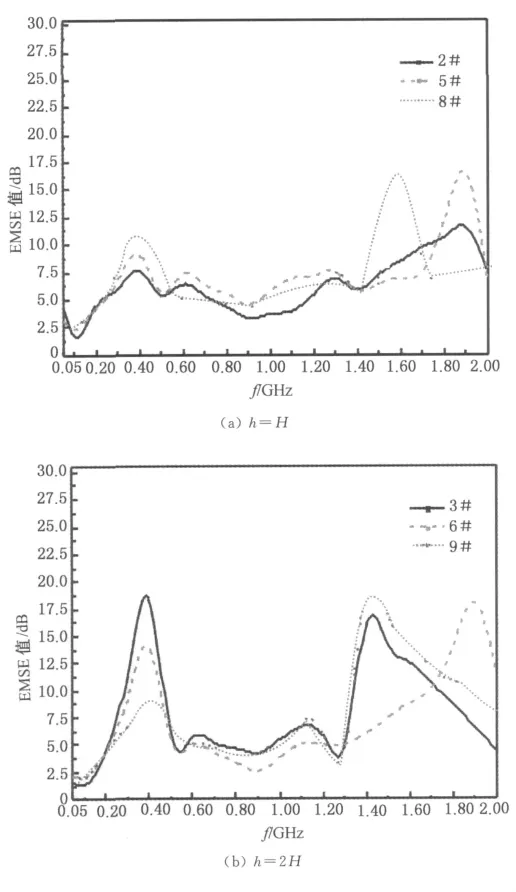
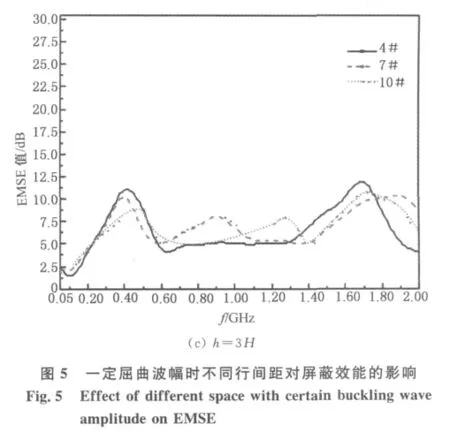
当试样的屈曲波幅h一定时，不同的行间距d对试样屏蔽效能的影响也不同.图5所示为不同屈曲波幅下纤维束的行间距d对屏蔽效能的影响.由图5（a）可知，屈曲波幅为H 时，2＃，5＃和8＃试样在低频段表现出极高的一致性，并随着行间距d的减小，即碳纤维含量的增多，特征峰依次增高；在高频段也有此特征，只是峰位置的移动，移动的机理有待表征，但至少与排布的密度有关，可能是声子晶体作用，其在某一频率范围内存在振动带隙［15－16］；中频段虽不太明显，但也有频率增大、屏蔽曲线上抬的趋势.

由图5（b）可知，屈曲波幅为2 H 时，试样的屏蔽效能曲线在低频段的趋势与图5（a）完全相反，3＃，6＃ 和9＃试样在低频段随着行间距d的减小，特征峰依次降低；在高频段的特征屏蔽峰的变化趋势与图5（a）该频段的趋势一致，并符合质量增多、屏蔽性能增大的规律，只是波幅为H的3＃试样的特征峰向右偏移；中频段的3条曲线因碳纤维质量增加而使得屏蔽性能增大的作用不明显.

图5（b）的结果说明，屏蔽特征峰的高低受频率的影响，而与碳纤维的质量变化无关.屏蔽特征峰值的移动，说明共振耗能的频率在变化，即对应的振动元的尺度、结合能和化学环境在发生变化.这显然与材料的组成即碳纤维含量多少无关，只与间隔尺寸或碳纤维长丝束间的相互作用距离有关.这是因为频率对应于波长，是共振尺度，也是吸收能量大小的表达［16］，因此屏蔽特征峰取决于材料的结构特征，而且更多的是声子晶体尺度与结构所表达的内容.

图5（c）所示为屈曲波幅最高为3 H 时，不同的行间距d对试样的屏蔽效能的影响.在低频段，特征屏蔽峰高，继续保持屈曲波幅为2 H时的特征，与碳纤维质量呈反比，但差异较小；在高频段也出现与质量呈反比的倾向，但差异亦较小，且峰的位置又开始趋于一致；在中频段，反而出现符合碳纤维质量增加、曲线上抬的趋势，且符合行间距d减小，碳纤维质量增多，屏蔽性能增大的原则.不过中频段曲线的上抬，也是由于出现特征峰所致，这说明有新的尺度振动元发生共振屏蔽.

2.4 综合评价指标

应用Origin软件以辐射源频率f、屈曲波幅h和行间距d对试样的屏蔽效能作显著性影响分析.

在试样行间距为10mm时，以辐射源频率f和屈曲波幅h为因素，进行方差分析.在显著性水平α＝0.05时，得Ff＝4.73＞3.49＝F1－α（2，20），Fh＝2.39＜3.49＝F1－α（2，20），所以辐射源频率对试样屏蔽效能的影响显著，而屈曲波波幅h对试样的屏蔽效能无显著影响.在试样屈曲波幅为H时，以辐射源频率f和间距d为因素，进行方差分析.在显著性水平α＝0.05时，得Ff＝18.99＞3.49＝F1－α（2，20），Fd＝2.14＜3.49＝F1－α（2，20），所以行间距d对试样屏蔽效能无显著影响，而辐射源频率f的影响显著.

由于辐射源频率作用影响显著，但不同频段的影响不尽相同，故采用低、中、高3段分散对比的方法来综合评价不同参数试样的屏蔽效能.先引入有效屏蔽能面积S指标如式（5）所示.

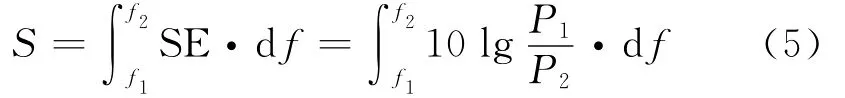
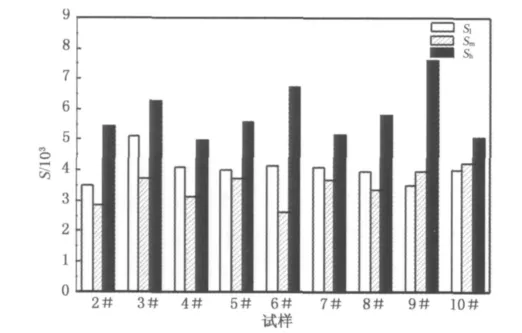
图6 试样在不同波段有效屏蔽面积对比Fig.6 The area of effective shielding energy of different samples in different frequency range

以0.6GHz为带宽，将测试频率范围按0.2～0.8GHz，0.8～1.4GHz，1.4～2.0GHz分为低、中、高3个频段来积分SE的面积S（Sl，Sm，Sh），并以此对各个试样的屏蔽效能进行综合评价，结果如图6所示.由图6可知，试样整体在高频段的屏蔽效能最好，在中频段最差.在低频段中，3＃试样表现出优良的屏蔽效能；在中频段中，各试样屏蔽效能相对都较低；在高频段中，9＃试样表现出优于其他试样的屏蔽效能.

3 结 语

本文通过测试间距为10mm，屈曲波波幅为H的碳纤维长丝束屈曲和平行排布的试样的电磁波屏蔽效能，结果表明屈曲排布和伸直排布的试样屏蔽效能不同，屈曲排布屏蔽效能大于伸直排布，这符合碳纤维填充质量的增加，屏蔽效能增加的规律.

碳纤维长丝束的不同屈曲波幅和排布行间距的影响分析表明，碳纤维质量的增加对屏蔽效能无显著影响，甚至在某些频段出现反比的结果；同时部分特征峰发生偏移，说明这类复合结构体的屏蔽性能在很大程度上取决于碳纤维的排布构形和堆砌密度，即屈曲波幅h和行间距d.

分频段的综合评价结果表明，辐射源频率、屈曲波幅和行间距对碳纤维屈曲排布屏蔽材料屏蔽性能有影响，频率的影响较为显著.引入有效屏蔽能面积S，以0.6GHz为带宽来分段评价试样在0.2～2.0GHz范围内的屏蔽效能，发现碳纤维/聚苯乙烯复合体在1.4～2.0GHz频段下屏蔽性能优异.屈曲波幅为2 H和间距为5mm的试样，在测试频率范围内的屏蔽性能较好.这对屏蔽材料的结构设计和对选择针对特定频段电磁波的防电磁波辐射具有指导价值.

［1］CHUNG D L.Electromagnetic interference shielding effectiveness of carbon materials［J］.Carbon，2001，39（1）：279－285.

［2］石风俊，郑德均.影响金属纤维混纺织物屏蔽效能因素初探［J］.毛纺科技，2006（11）：43－44.

［3］CHENG K B，LEE M L，RAMAKRISHNA S，et al.Electromagnetic shielding effectiveness of stainless steel/polyester woven sabrics［J］.Textile Research Journal，2001，71（1）：42－49.

［4］LEE S E，PARK K Y，OH K S，et al.The use of carbon/dielectric fiber woven fabrics as filters for electromagnetic radiation［J］.Carbon，2009，47（8）：1896－1904.

［5］SOYALSAN D，CÖMLEKCI S，GÖKTEPEÖ.Determination of electromagnetic shielding performance of plain knitting and 1×1rib structures with coaxial test fixture relating to ASTM D4935［J］.Journal of the Textile Institute，2010，101（10）：890－897.

［6］PENG Z H，CAO M S，YUAN J，et al.Strong fluctuation theory for effective electromagnetic parameters of fiber fabric radar absorbing materials［J］.Materials and Design，2004，25（2）：379－384.

［7］FOLGUERAS L D C，NOHARA E L，et al.Dielectric microwave absorbing material processed by impregnation of carbon fiber fabric with polyaniline［J］.Materials Research，2007，10（1）：95－99.

［8］TELLAKULA R A，VARADAN V K，SHAMI T C，et al.Carbon fiber and nanotube based composites with polypyrrole fabric as electromagnetic absorbers［J］.Smart Materials and Structures，2004，13（5）：1040－1044.

［9］邹田春，赵乃勤，师春生，等.微量碳纤维/树脂复合吸波材料的研究［J］.功能材料，2005，36（11）：1689－1692.

［10］ZHENG T L， WANG Y H，ZHENG K Y，et al.Electromagnetism and absorptivity of the modified micro－coiled chiral carbon fibers［J］.Chinese Journal of Aeronautics，2007，20（6）：560－563.

［11］HORVATH J S.Expanded polystyrene（EPS）geofoam：An introduction to material behavior ［J］. Geotextiles and Geomembranes，1994，13（4）：263－280.

［12］ASTM D4935—1999，Standard test method for measuring the electromagnetic shielding effectiveness of planar materials［S］.

［13］VARNAITE S.The use of conductive yarns in woven fabric for protection against electrostatic field［J］.Materials Science，2010，16（2）：133－137.

［14］CHEN H C，LEE K C，LIN J H，et al.Comparison of electromagnetic shielding effectiveness properties of diverse conductive textiles via various measurement techniques［J］.Journal of Materials Processing Technology，2007，192：549－554.

［15］WEI R J，WU B，HE C F，et al.Phononic band structure in a two－dimensional hybrid triangular graphite lattice［J］.Physica B：Condensed Matter，2009，404（20）：3795－3798.

［16］ARMENISE M，CAMPANELLA C E，CIMINELLI C，et al.Phononic and photonic band gap structures：Modeling and applications［J］.Physics Procedia，2010，3（1）：357－364.

Effect of Carbon Filaments Buckling Waved Arrangement on the Shielding Property of Electromagnetic Wave

WU Yu1，ZHOU Sheng2，XU Zeng－bo3，YU Wei－dong1
（1.College of Textiles，Donghua University，Shanghai 201620，China；2.Department of Textile and Clothing，Yangzhou Polytechnic College，Yangzhou Jiangsu 225012，China；3.Fashion College of Technology，Shanghai University of Engineering Science，Shanghai 201620，China）

Based on a carbon filaments buckling waved arrangement model for electromagnetic wave（EMW）shielding materials，the effects of the frequency of radiation source，buckling wave amplitude of carbon filaments and space between the carbon filaments on the shielding property of this model in the microwave range were discussed.The results showed that the effect of frequency factor of radiation source was significant and there existed a better EMW shielding property of the shielding material in which the waved carbon filaments were arranged on the frequency of 1.4～2.0GHz.The effects of the structural parameters，including the amplitude of buckling wave and the space between carbon filaments were significant on EMW shielding，especially for 2 Hbuckling wave amplitude and 5mm space.While there was no obvious change of EMW shielding property with the carbon filaments content.

carbon filaments；buckling waved arrangement；electromagnetic wave；shielding property；effective shielding energy

TS 101.3

A

2011－06－03

扬州市科技计划资助项目（YZ2007100）

吴 瑜（1988—），女，湖北荆州人，硕士，研究方向为碳纤维集合体电磁屏蔽材料.E－mail：yuwu1988＠mail.dhu.edu.cn于伟东（联系人），男，教授，E－mail：wdyu＠dhu.edu.cn

1671－0444（2012）03－0256－05