基于马尔可夫链的易变性职业转移模型研究

符谢红

（东华大学 旭日工商管理学院，上海 200051）

基于马尔可夫链的易变性职业转移模型研究

符谢红

（东华大学 旭日工商管理学院，上海 200051）

当传统职业生涯逐渐向易变性职业生涯转变，职业的转移为多方向性、动态性和不可预测性.基于职业发展的混沌理论，尝试探索易变性职业路径规律的定量描述，将易变性职业看成一随机过程，运用马尔可夫链模型，选取营销资深人员的职业路径作为研究样本，建立易变性职业转移模型，并进行算例分析，从而得到职业转移“整体模式稳定性”的规律.结果显示易变性职业转移模型具有良好的适用性，该职业转移模型在理论上是对易变性职业生涯定量研究的有益补充，并在人力资源领域，特别是揭示人才成长规律方面具有实践意义.

马尔可夫链；易变性职业转移模型；营销资深人员

工作的每次转移形成了职业路径的特点，不同职业的路径特点各不相同.对某一特定职业的路径特点进行规律研究有助于人力资源管理和开发.从宏观层面上，职业路径规律为国家人才培养政策的实施提供帮助；在企业微观层面上，职业路径规律为企业人力资源规划和开发提供依据；对“渺观”的个体而言，职业路径规律是个体自我职业指导的重要基础.随着我国经济的发展，职业也在不断地变化，个体的职业观更加自主，路径规律也在变化，持续关注职业路径的规律就显得更加重要.

HALL［1］最早提出了易变性职业生涯的概念并致力于该领域的研究.易变性职业生涯与传统职业生涯相比，在职业成功的标准、心理契约、职业流动模式、职业生涯管理责任方面都有着完全不同的改变.当易变性职业生涯不断盛行，传统以组织为主导的职业生涯逐渐消失.BARUCH［2］提出易变性职业路径的多方向性模型包含了职业的多种选择、多种可能的发展方向、多种职业成功的定义，职业的转移为多方向性和动态性.

职业路径的研究起源于职业生涯规划.职业路径是一个人一系列工作经历所形成的路径，是关于时间的函数，即对每一个时间段上的一系列工作的连续性考察，可以反映出有关职业经历的过程或结果.营销人员的职业路径各不相同，职业发展呈现出多方向性的特点，运用营销职业分析易变性职业路径具有代表性.营销资深人员个体的职业路径，不仅可以反映出他的工作经历，还可以透过职业路径上的某一点来察看某一时间点上他所处的行业环境、组织环境和个人环境，所以具体的职业路径可以反映规律.BLOCH［3］明确将混沌理论的概念引入职业领域，指出职业发展是一个复杂的适应性实体.职业发展的混沌理论强调非线性系统分析的研究范式.混沌理论研究的关键就是要发现隐藏在不可预测的无序现象里的内部有序结构，使学者们有可能进一步探索用现有范式所不能描述、解释或预测的现象.职业发展的混沌理论中的分形特点就提供了探询规律的可行性［4］.

YOUNG等［5］较早运用转移概率矩阵分析和预测企业内部人员的分布.近几十年来转移概率模型已被企业运用于分析内部人力资源的流动趋势和概率，如升迁、转职、调配或离职等方面的情况，以便为内部的人力资源的规划提供依据.相关研究如GEORGIOU等［6］运用马尔可夫链建立人力资源规划的招聘培训模型.以往的研究采用定量分析的方法，在预测人员供给方面有成熟的运用，但研究范围局限在企业内部.本文建立职业转移发展概率模型，将运用延伸到特定的职业、跨边界的工作、宏观的劳动力市场中，同时建立职业转移来源概率模型对某一特定职业的来源特点进行规律研究，有利于揭示人才成长规律.

1 职业转移的马尔可夫链模型

FORD等［7］提出了发展系统理论（DST），认为个人的职业发展方向是开放的、不可预测的，而且发展的道路在一生中会有显著的变化.职业发展的混沌理论将职业的转移在理论上看作是一随机过程，即个体职业转移的概率只依赖于最近时期职业的状态，而与前期的职业状态无关，这样，职业转移可视为马尔可夫过程分布，即当系统在时刻T＝｛0，1，2，3，…｝所处的状态为已知的条件下，过程在时刻t＞t0所处的状态与其在t0时刻之前所处的状态无关.职业转移的理论假设与离散参数马尔可夫链模型的假设一致，因此，建立马尔可夫链模型对特定职业的转移概率进行算例分析是可行的.本文专注于职业转移规律的定量描述，研究的问题是营销人员职业历程的规律.不仅要分析营销职业的发展概率，同时分析其来源概率，因此建立两个模型分别讨论.

1.1 职业转移发展概率模型

离散参数马尔可夫链是指状态空间E和参数集T都是离散的马尔可夫过程，记作｛Xn｝，n＝0，1，2，….用E＝ ｛in1，in2，in3，…｝表示马尔可夫链的状态空间，T＝｛0，1，2，3，…｝表示参数集，则马尔可夫链模型的性质：

对于任意非负整数k及n1＜n2＜…＜ni＜m，

式（1）表示工作从m时刻的状态im转移到m＋k时刻的状态im＋k的概率，并简记为pij（m，m＋k）.如果pij（m，m＋k）只与i，j，k有关，则称其具有齐次性，记为pij（k），称pij（k）为k步转移概率.用一个矩阵把所有转移概率表示出来，即p（k）＝（pij（k）），即p（k）为k步转移概率矩阵［8］.

关于职业的分类本文借鉴了国家职业分类标准，职业编码参考了第五次全国人口普查所使用的职业分类与代码表.通过对营销资深人员经历的每个职业进行编码，根据结果汇总归纳出7种职业大类——营销、综合管理、技术、生产运作、教育、行政后勤及其他.各职业分类分别依次用数字i＝1，2，3，…，7表示.在这些营销资深人员的职业历程中，pij表示从初始状态i转移到新状态j的概率，如p11，p21，p31，p41，p51，p61，p71分别表示营销、综合管理、技术、生产运作、教育、行政后勤及其他职业转移到营销的概率；p12，p22，p32，p42，p52，p62，p72分别表示营销、综合管理、技术、生产运作、教育、行政后勤及其他职业转移到综合管理的概率，依此类推.职业转移发展概率P是一个7×7矩阵，它概括了营销资深人员的职业经历，反映了其职业转移发展规律，如式（2）所示.

此外，Πn表示在第n次转移从事的职业类型j的概率矩阵，πj表示第n次转移从事的职业类型j的概率，其中，j＝1，2，3，…，7，分别表示7种不同的职业类型.即

根据马尔可夫链的性质，不可约非周期有限马尔可夫链必存在平稳分布，且平稳分布就是极限分布.理论上易变性职业转移的马尔可夫链具有不可约和非周期性的特点，因此存在平稳分布.即

1.1.3 子宫肌瘤 子宫肌瘤是女性生殖系统常见的良性肿瘤，可引起经量异常增多、继发贫血、盆腔疼痛等，还可以改变子宫的解剖结构，进而影响子宫的收缩、蠕动以及内膜的容受性。据统计，以子宫肌瘤作为不孕唯一因素的占不孕女性的1%～3%[19-21]。肌瘤类型不同影响妊娠的机制也不同。有研究认为，黏膜下肌瘤是导致不孕的首要因素[22]。黏膜下肌瘤可影响宫腔面积和血供，使妊娠率和分娩率降低；肌壁间肌瘤对于妊娠和分娩的影响并不明显；而浆膜下肌瘤对于妊娠和流产无明显影响[23]。肌瘤的生长部位对于妊娠也有影响，前壁及后壁的肌瘤较其他部位的肌瘤对妊娠的影响小[24]。

且

如果对所有的im，im＋k∈I，

所以

无论现时刻从什么状态出发，经过足够多步运算以后到达im＋k的发展概率都为πj，与现时刻状态im无关，则称该马尔可夫链具有平稳性.

营销人员职业转移在最终均衡状态时从事7类职业的概率如式（8）所示.

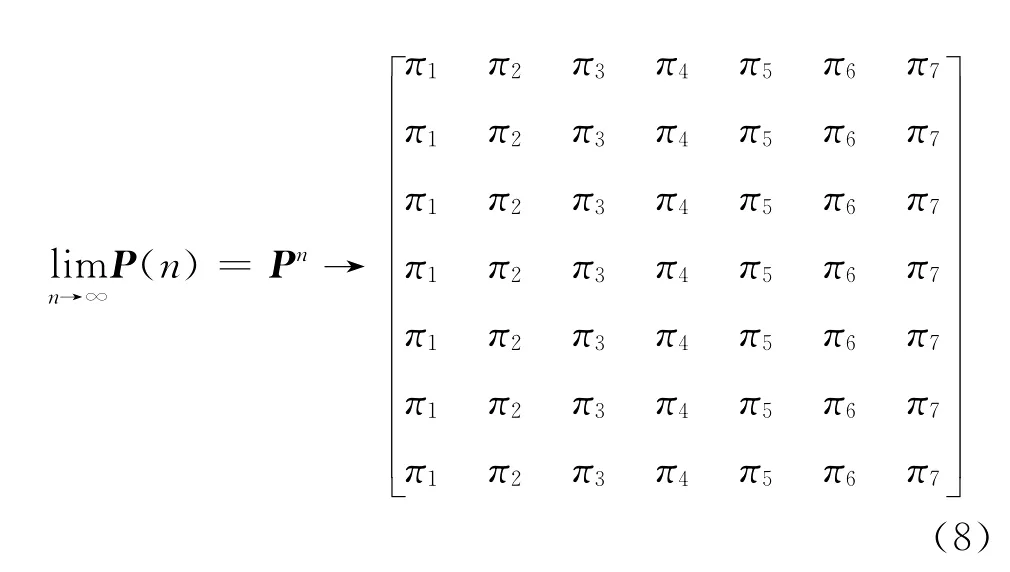
1.2 职业转移来源概率模型

本文的样本为营销资深人员，研究的问题是他们的职业历程和职业来源规律，因此，本模型借鉴马尔可夫链模型的逆过程来探究职业转移的来源概率.

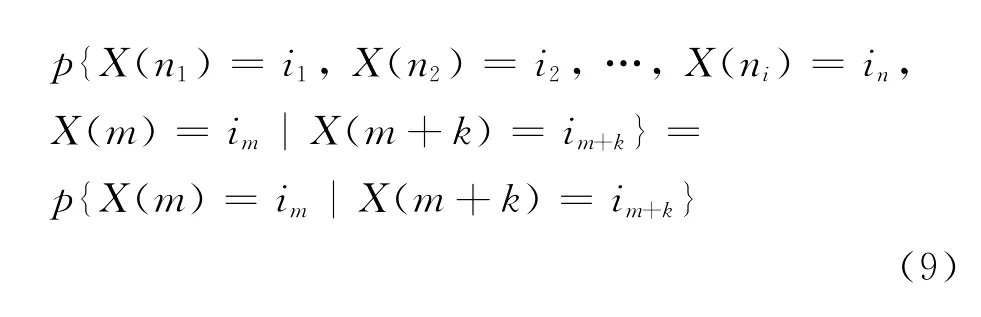
式（9）表示工作从m＋k时刻的状态im＋k逆转移到m 时刻的状态im的来源概率，并简单记为pij（m＋k，m）.

此外，Πn表示在第n次逆转移从事职业类型i的概率矩阵，πi表示在第n次逆转移从事职业类型i的概率，其中，i＝1，2，3，…，7分别表示7种不同的职业类型.即

职业来源概率矩阵与职业发展概率矩阵同样属于不可约非周期有限马尔可夫链，必存在平稳分布，且平稳分布就是极限分布，但它们平稳分布形式上的不同表现在来源矩阵横数列相同而发展矩阵纵数列相同.

如果对所有的im，im＋k∈I，

所以

无论现时刻从什么状态出发，经过足够多步逆运算以后到达im的来源概率都为πi，与现时刻状态im＋k无关，则称该马尔可夫链具有平稳性.营销职业转移来源矩阵最终均衡状态如式（16）所示.

2 实证分析和理论解释

2.1 研究设计与样本分析

本文于2010年7月及2011年7月对118名正在从事或者曾经从事营销工作的资深专业人员进行深度访谈.访谈依据半结构化的职业探索访谈提纲进行，内容针对职业经历和职业变动，并形成文本记录，最终获得有效样本99个.在被访问者中综合管理者占34%，营销管理者占64%，其他管理人员占2%；男性占78%，女性占22%；工作年限在4～9年的被访者占37.4%，工作年限在10～19年的被访者均占41.4%，工作年限在20～46年以上的占21.2%.由此可见，被访对象的工作年限较长.因本访谈样本为营销资深人员，适合运用于来源概率模型，从而研究其成长规律.

研究运用质性方法对访谈记录进行分析.通过对样本的每一个职业进行编码，用Xi，j（i，j＝1，2，3，4，5，6，7）表示职业i转移到职业j的频率，数据整理得出有效样本共发生职业转移263次.以矩阵形式表示转移类型的频率，如式（17）所示.

将式（17）中的每个数除以矩阵内所有数之和，对应得到职业转移类型概率矩阵，如式（18）所示.

由式（18）可以看出，p11最大，明显高于次大值p12，其次为p31，p22，p61，p41，p21，p66.其余概率的值显著减小且均小于0.020.观察矩阵特点，对

根据以上数据可知，样本中营销资深人员的职业转移历程中，概率p11最大，为0.483，即48.3%的职业转移类型为营销转到营销；概率p12次之，为0.107，即10.7%的职业转移类型为营销转到综合管理，即7种职业转入营销的转移频率之和占总转移频率的比例为67.7%.所得结果与本文被访对象的职业特征是非常吻合的，即营销资深人员的工作变换中，营销内部的转移占了近一半.样本的工作转移中67.7%为转入营销，因此分析来源概率矩阵时以分析pi1为主.

2.2 营销职业转移来源概率模型实证

将式（17）中的每个数除以每列数之和，对应得到营销职业转移的来源概率.则一步来源概率矩阵P如式（19）所示.

由式（19）可知，对于市场营销资深人员，职业转移来源概率pi1中最大的是p11，为0.713 5，其次是p31为0.101 1，再次是p61，p41和p21，分别为0.056 2，0.050 6和0.044 9，最小的概率是p51和p71，均为0.016 9.由此可以得出营销职业来源概率的大小关系：营销来源于营销＞营销来源于技术＞营销来源于行政后勤＞营销来源于生产运作＞营销来源于综合管理＞营销来源于教育＝营销来源于其他，其中营销来源于营销的概率远远大于来源于其他职业的概率.这是因为资深营销人员多经历了从初级营销工作到中高级营销工作的转移.

在此基础上，可以通过一步转移概率矩阵，预测前一个工作所属职业的概率.例如，某个体的第3个工作属于营销，那么其第2个工作有71.35%的概率从事营销；有10.11%的概率从事技术；有5.62%的概率从事行政后勤；有5.06%的概率从事生产运作；有4.49% 的概率从事综合管理；分别有1.69%的概率从事教育和其他类职业.

当转移次数趋于无穷时，根据n步转移概率矩阵的平稳性质，得到最终的均衡概率πi（i＝1，2，3，4，5，6，7），如式（20）所示.

将式（19）代入式（20）得到：

以方程式形式表达如式（21）所示.

联立方程（21）和（22），在 Matlab中可以采用高斯消去法［9］进行求解，计算结果为π1＝0.550 8，π2＝0.086 1，π3＝0.123 1，π4＝0.118 8，π5＝0.021 0，π6＝0.077 1，π7＝0.023 0.即

可以看出，无论初始状态如何，经过若干次转移以后，达到最终均衡状态的概率是稳定的.即营销职业有55.08%的概率来源于营销职业；12.31%的概率来源于技术；11.88%的概率来源于生产运作；8.61% 的概率来源于综合管理；7.71%的概率来源于行政后勤；2.10%来源于教育；2.30%来源于其他.综上所述，通过来源概率矩阵分析营销资深人员的职业历程，有两个特点：（1）营销职业来源于营销职业的概率最大，占到了半数以上，说明资深营销人员需要营销经验的积累，大多经历了从初级营销工作到中高级营销工作的转移；（2）营销职业的转移来源较广，包括技术、生产运作和行政后勤等职业，一方面营销初级工作的入门对通用能力的要求较高，但专业门槛不高，另一方面在其他职业上积累的有关产品、技术和组织的知识对营销工作的绩效有较大帮助.

3 结 语

本文运用马尔可夫链反映易变性职业转移中的随机性，通过建立职业转移发展概率模型和职业转移来源概率模型揭示其中的规律，从而反映职业转移规律整体的稳定性.选取了营销资深人员的职业路径作为样本，建立职业转移来源概率模型，并进行算例分析其职业转移的规律，所得结果显示模型具有良好的适用性.

本研究的不足之处在于算例样本数量较少，样本范围仅为营销资深人员.进一步的研究可以增加样本职业类型进行的分析；细分不同时间段或不同年龄段的职业转移，得出的规律可更加精确反映现状；以薪酬或以心理满足感作为职业阶段的分类依据，可反映其他维度的职业发展.

［1］HALL D T.Protean careers of the 21st century［J］.Academy of Management Executive，1996，10（4）：8－16.

［2］BARUCH Y.Trans forming careers：From linear to multi directional career paths［J］.Career Development International，2004，9（1）：58－73.

［3］BLOCH D P.Complexity，chaos，and nonlinear dynamics：A new perspective on career development theory［J］.The Career Development Quarterly，2005，53（3）：194－207.

［4］周满玲，张进辅，曾维希.职业发展的混沌理论［J］.心理科学进展，2006，14（5）：739－741.

［5］YOUNG A，ALMOND G.Predicting distribution of staff［J］.Computer Journal，1961，3（4）：246－250.

［6］GEORGIOU A C，TSANTAS N.Modelling recruitment training in mathematical human resource planning［J］.Applied Stochastic Models in Business and Industry，2002，18（1）：53－74.

［7］FORD D H，LERNER R M.Developmental systems theory：An integrative approach［M］.Thousand Oaks，CA：Sage Publications，Inc，1992：259.

［8］陈良均，朱庆堂.随机过程及运用［M］.北京：高等教育出版社，2003：10.

［9］高会生，刘童娜，李聪聪.MATLAB实用教程［M］.2版.北京：电子工业出版社，2010：263.

Research on Protean Career Mobility Model Based on Markov Chain Approach

FU Xie－hong
（Glorious Sun School of Business and Management，Donghua University，Shanghai 200051，China）

With the traditional career change to the protean one，the transforming careers become multi directional，dynamic and unpredictable.Based on stochastic theory，the mathematical patterns were set up to revealing protean career transformation law.Tracking randomness of the protean career by using the Markov chain，the protean career mobility model was set up to reflect its overall stability by giving marketing seniority as the application of the model.The conclusion showed that the protean career mobility model had good applicability.The model contributes to the quantitative study of a protean career.The exploratory findings have important application in human recourse management，specifically in revealing the law of talents growth.

Markov chain；protean career mobility model；marketing seniority

F 224；F 240

A

2012－03－30

中央高校基本科研业务费专项资金资助项目

符谢红（1973—），女，海南海口人，讲师，博士研究生，研究方向为人力资源管理.E－mail：fxh＠dhu.edu.cn

1671－0444（2012）03－0338－06