改进型耗散粒子群优化算法

姜长元，赵曙光，郭力争，冀 川

（1.东华大学 信息科学与技术学院，上海 201620；2.湖州师范学院 理学院，浙江 湖州 313000）

改进型耗散粒子群优化算法

姜长元1，2，赵曙光1，郭力争1，冀 川1

（1.东华大学 信息科学与技术学院，上海 201620；2.湖州师范学院 理学院，浙江 湖州 313000）

通过对标准粒子群优化算法中惯性权重的分析和对耗散理论的研究，提出了一种惯性权重正弦调整的耗散粒子群优化算法（S－DPSO），并对该算法进行了深入的分析和研究.通过对4个典型函数的仿真测试，试验结果表明S－DPSO在收敛速度和全局收敛性方面都比标准粒子群优化算法、随机惯性权重粒子群优化算法、惯性权重正弦调整粒子群优化算法、耗散粒子群优化算法和随机惯性权重耗散粒子群优化算法有明显改进.理论分析和仿真试验验证了S－DPSO的正确性和有效性.

粒子群优化算法；惯性权重；正弦调整；耗散；跳变因子

粒子群优化（particle swarm optimization，PSO）算法是1995年由美国社会心理学家KENNEDY和电气工程师EBERHART基于鸟群觅食行为而提出的群体智能进化算法［1－2］.该算法由于具有概念简明、参数简单、收敛速度快、实现方便等特点，受到了很大的关注.加入惯性权重的PSO算法现已成为常用的标准PSO算法.目前，PSO算法已成为一个研究热点，通常用于多目标优化、神经网络参数训练、智能系统控制等方面［3－5］.

由于标准PSO算法更像粒子的聚类，粒子向当前最好位置的方向飞行，导致多样性缺失，适应值停滞，尤其在进化后期缺乏改进解的能力［3］.国内外学者提出了多种改进算法［2－8］.标准PSO算法在前期具有较好的全局搜索能力，后期收敛性也较好，但收敛速度比较慢；随机惯性权重粒子群优化（R－PSO）算法［4］虽然前期收敛速度很快，但后期的局部搜索能力较差.本文研究惯性权重ω对算法性能的影响以及耗散理论对解的多样性贡献，提出一种惯性权重正弦调整的耗散粒子群优化（S－DPSO）算法.通过仿真测试，S－DPSO算法在收敛速度和全局收敛性方面均优于标准PSO算法、R－PSO算法、惯性权重正弦调整粒子群优化（S－PSO）算法、耗散粒子群优化（DPSO）算法和随机惯性权重耗散粒子群优化（R－DPSO）算法.

1 标准PSO算法

PSO算法采用进化算法中群体和进化的概念.随机初始化一群没有体积、没有质量的粒子，将每个粒子视为优化问题的一个可行解，粒子的好坏由一个事先设定的适应度函数来确定.每个粒子在可行解空间中运动，由一个速度变量决定其方向和距离.粒子根据自身的最优位置和整个粒子群全体的最优位置，调节自身的飞行方向和速度，一直朝目前的最优粒子飞行［2－4］.

粒子群进化过程可用下面两个方程描述.

其中：r1，r2为均匀分布在（0，1）区间的随机数；c1，c2称为学习因子，通常取c1＝c2＝2，在式（1）中，为简化，常常记φ1＝c1r1，φ2＝c2r2；ω称为惯性权重.根据式（1）和（2）对粒子的速度、位置不断更新进化，直到满足最大迭代次数或者满足所要求的精度才停止迭代.

式（1）右侧第一项为粒子先前速度的继承，依据自身的速度进行惯性运动；第二项为“认知”部分，结合自身以往的经历实现下一步行为决策；第三项为“社会”部分，表示粒子间的信息共享与合作.

2 改进型耗散粒子群优化算法

2.1 S－PSO算法

通过对各种改进的粒子群优化算法的分析研究、仿真［2－8］可知，惯性权重ω对算法性能有以下影响：较大的ω值有利于跳出局部最优，进行全局寻优；较小的ω值有利于局部寻优，加速算法收敛.

本文提出一种惯性权重正弦调整的粒子群优化算法：

取φ1＝ （ω（t）＋1）r1，φ2＝ （ω（t）＋1）（2－r1）r2，文献［9－11］中提到的所有条件均能得到满足，从理论上说明了S－PSO算法在收敛性能上有一定的保障.

由ω值的变化可知，在算法开始时，让粒子在其自身附近作局部寻优，在一段时间后加大互相协作程度，进行全局寻优，最后让最优粒子进行局部搜索.

2.2 耗散粒子群结构

耗散结构是指处在远离平衡态的开放系统，通过与外界交换物质和能量，在一定的条件下通过自组织形成一种新的稳定的有序结构.文献［12］首先实现了将耗散结构引入粒子群算法中，提出了耗散粒子群算法.在耗散粒子群算法中，通过对粒子速度、位置的跳变来完成对系统的耗散过程［13－14］.具体实现如式（3）和（4）所示.

其中：cv和cl为跳变因子，其值在［0，1］内；random（Ld，Ud）为Ld与Ud之间的随机数.在随机数小于这两个跳变因子的情况下，速度和位置进行跳变，这样可以防止系统达到暂时平衡态，也就是算法陷入局部最优的情况.

式（3）和（4）的两步跳变在速度与位置更新之后.

2.3 算法分析

本文提出的惯性权重正弦调整的耗散粒子群优化算法，在速度迭代过程中，当粒子逐渐接近最好位置的过程中，式（1）的后两项逐渐趋近于0，如果，速度的变化将完全依靠式（1）的即如果粒子到达全局最佳位置之后，还要继续移动，必须保持原速度和权值ω都不为0.如果先前的速度已非常接近于0，那么粒子一旦达到全局最佳位置，它们的运动将趋向停滞状态，粒子将一直在一个位置周围运动，称这样的算法是不完全收敛的［13－14］.

标准PSO算法之所以搜索精度不高，是因为粒子速度下降至0时，所搜索到的解尚未达到全局最优.耗散粒子群优化算法为了解决这个问题，用随机数与一个适当的跳变因子进行比较，在满足比较条件的情况下，加入负熵对速度进行耗散，保持系统处于远离平衡的状态.耗散粒子群优化算法并没有改变标准PSO算法的基本结构，主要更新机制与标准PSO算法相似，只是通过对粒子的不断耗散来增加种群的多样性，从而提高算法的搜索性能.因此，耗散粒子群优化算法会收敛于个体历史最优和群体最优中的某个权平衡点.

耗散粒子群优化算法每一次迭代更新产生的结果值是否需要进行耗散与随机数和跳变因子比较结果有关，目前跳变因子的选择主要依据经验值.

3 仿真实例

3.1 仿真设置

为了能进一步比较，选取一种随机变化惯性权重粒子群优化算法［4］，即ω＝0.4＋rand（）/2，在整个迭代过程中，ω值的变化范围均为［0.4，0.9］.

待测试算法有PSO，R－PSO，S－PSO，将其分别加入耗散结构后又得3种：DPSO，R－DPSO，SDPSO，共计6种算法.

为验证新算法的性能，采用文献［2］中所提及的Benchmark的4个常用测试函数，如式（5）～（8）所示，用6种算法进行测试，统计收敛率、收敛代数与平均最优适应度.

f1是Sphere函数：

f2是Rosenbrock函数：

f3是Rastrigrin函数：

f4是Griewank函数：

其中：f1是单峰函数，全局最小值为0，收敛于（0，0，…，0）；其余3个函数均是经典的多峰函数，全局最小值为0，f2收敛于 （1，1，…，1），f3和f4收敛于 （0，0，…，0）.

在对4个测试函数仿真试验的各PSO算法中，取c1＝c2＝2；最大进化代数取为1 500；群体规模为40；跳变因子cv＝cl＝0.1；各个函数的vmax取为变量范围的上限.对每个算法，各运行20次，取平均适应度、平均最优结果，收敛率、收敛代数为评价数据.其他测试参数如表1所示.测试机器为Pentium Dual 1.8G，2G内存，采用 Matlab 7.0编程.

表1 4个函数的测试参数Table 1 Test parameters for four functions

3.2 结果分析

4个测试函数20次试验平均最优解随迭代次数的变化历程如图1～4所示.从图1～4可以看出，若不加入耗散结构，S－PSO算法收敛性优于PSO算法和R－PSO算法.本文提出的S－DPSO算法在迭代前期有很强的收敛性，在1/5迭代时期即已获得理想值，尤其是图2（b），3（b），4（b），其强收敛性更具说服力，且在后续迭代过程中始终能保持优势.在图3（a）中，PSO 算法、R－PSO 算法、S－PSO 算法不能很好收敛到最优解附近，而加入耗散结构后，算法收敛性立即得到较大改善，且以S－DPSO算法收敛性最好，见图3（b）.若针对某一函数，将6种算法的仿真测试结果放在一起，也有很好的表现效果.当然，若增加迭代次数，算法还将进一步收敛.表2是仿真结果，从平均最优迭代结果和收敛代数来看，S－DPSO算法均比其他5种算法要好.在仿真试验中，通过改变维数、迭代次数、群体规模、跳变因子等，S－DPSO算法在相同条件下多次测试均取得较理想结果，这说明在针对4个测试函数方面，本文提出的S－DPSO算法能够加快收敛速度，使收敛精度变高.

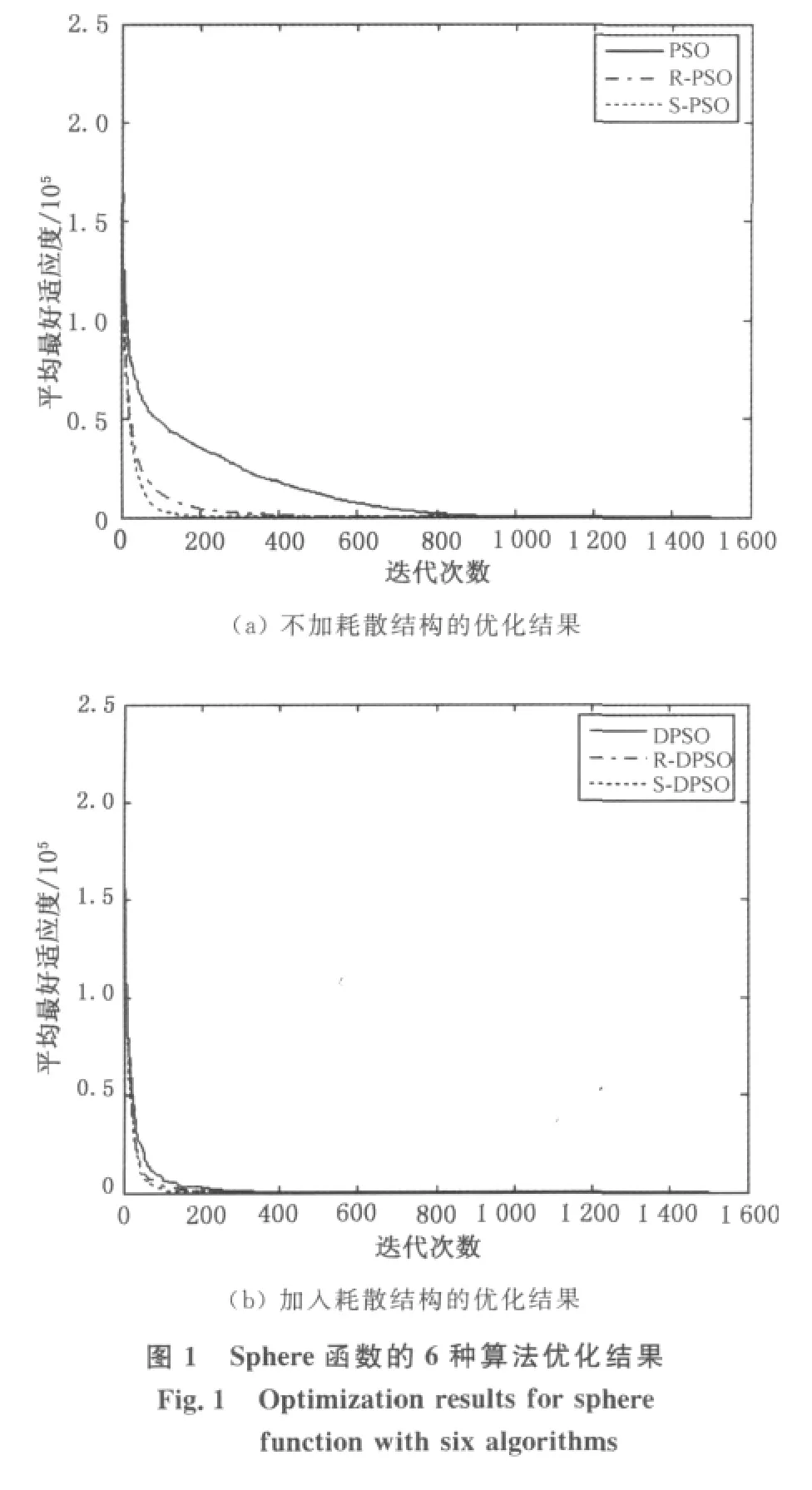
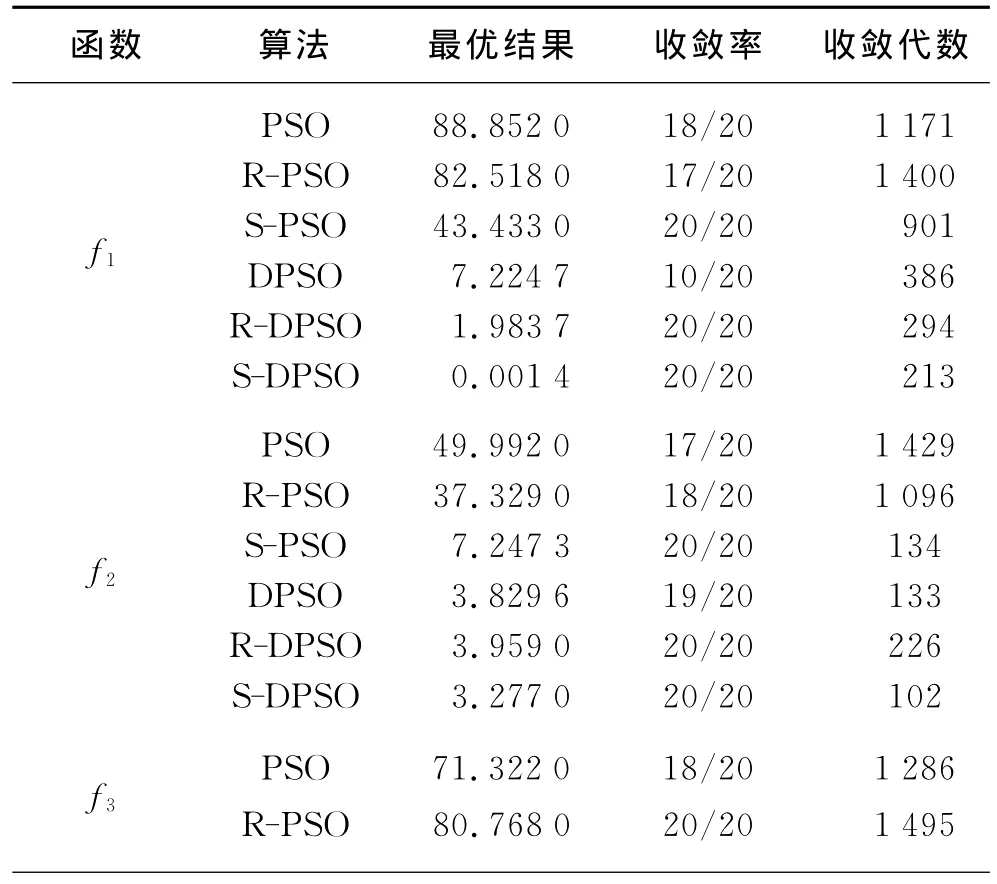
表2 4个函数6种算法的平均测试结果Table 2 Testing average results for four functions with six algorithms

续 表

4 结 语

粒子群优化算法是一种新型的进化算法，在算法收敛速度以及惯性权重调整方面还有很多值得研究的问题.本文通过分析惯性权重调整方法对收敛速度的影响以及耗散理论对解的影响，提出了一种惯性权重正弦调整的耗散粒子群优化（S－DPSO）算法，并且利用 PSO，R－PSO，S－PSO，DPSO，R－DPSO，S－DPSO算法对4种典型测试函数进行仿真试验，试验结果表明，S－DPSO算法比其他5种PSO算法收敛速度更快、收敛精度更高.

［1］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings IEEE International Conference on Neural Networks.Piscataway NJ：IEEE Service Center，1995：1942－1948.

［2］SHI Y，EBERHART R C.Empirical study of particle swarm optimization［C］//Proceedings of Congress on Evolutionary Computation.Washing DC，1999：1945－1950.

［3］EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory ［C ］//Proceedings of the 6th International Symposium on Micro Machine and Human Science.Piscataway NJ：IEEE Service Center，1995：39－43.

［4］李丽，牛奔.粒子群优化算法［M］.北京：冶金工业出版社，2009.

［5］韩江洪，李正荣，魏振春.一种自适应粒子群优化算法及其仿真研究［J］.系统仿真学报，2006，18（10）：2969－2971.

［6］胡建秀，曾建潮.微粒群算法中惯性权重的调整策略［J］.计算机工程，2007，33（11）：193－195.

［7］TRELEA I C.The particle swarm optimization algorithm：Convergence analysis and parameter selection［J］.Information Processing Letters，2003，85（6）：317－325.

［8］SHI Y，EBERHART R C.Parameter selection in particle swarm optimization ［C］//Proceeding of Seventh Annual Conference on Evolutionary Computation.Washing DC，1998：591－600.

［9］李宁，孙德宝，邹彤，等.基于差分方程的PSO算法粒子运动轨迹分析［J］.计算机学报，2006，29（11）：2052－2061.

［10］CLERC M，KENNEDY J.The particle swarm－explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Transactions on Evolutionary Computation，2002，6（1）：58－73.

［11］XIE X F，ZHANG W J，YANG Z L.A issipative article warm optimization ［C］//The IEEE Congress on Evolutionary Computation，Hawaii，2002：1456－1461.

［12］任小波，杨忠秀.耗散粒子群算法的性能分析［J］.计算机仿真，2010，27（2）：204－207.

［13］孟凡辉，王秀坤，赫然，等.一种改进的耗散粒子群算法［J］.计算机工程与应用，2005（12）：34－36，69.

［14］SHEN X F，WEI K P，WU D M，et al.A dynamic adaptive dissipative particle swarm optimization with mutation operation［C］//2007IEEE International Conference on Control and Automation.Guangzhou，2007：586－589.

An Improved Dissipative Particle Swarm Optimization Algorithm

JIANG Chang－yuan1，2，ZHAO Shu－guang1，GUO Li－zheng1，JI Chuan1
（1.College of Information Science and Technology，Donghua University，Shanghai 201620，China；2.School of Science，Huzhou Teachers College，Huzhou Zhejiang 313000，China）

Based on the analyzing inertia weight of the standard particle swarm optimization（PSO）algorithm and studying the dissipative structure theory，a new dissipative PSO（DPSO）algorithm with sinusoidal changing inertia weight（S－DPSO）is presented.S－DPSO algorithm is conducted in－depth analysis and research.By the experiments of four benchmark function，the results show the performance of S－DPSO improve more clearly than the standard PSO，random inertia weight PSO（R－PSO），S－PSO，DPSO and R－DPSO.Theoretical analysis and simulation experiments show that the S－DPSO is efficient and feasible.

particle swarm optimization algorithm；inertia weight；sinusoidal changing；dissipative；chaotic factors

TP 301.6

A

2011－05－27

浙江省教育厅基金资助项目（Y201016350）；湖州市自然科学基金资助项目（2010YZ05）；浙江省自然科学基金资助项目（Y6110043）

姜长元（1975—），男，安徽安庆人，讲师，博士研究生，研究方向为控制理论与控制工程.E－mail：jcy＠hutc.zj.cn

赵曙光（联系人），男，教授，E－mail：sgzhao＠dhu.edu.cn

1671－0444（2012）03－0312－06