精切齿轮铣刀刀片切削刃廓形求解与误差浅析

张国福 王晓峰

（①哈尔滨第一工具制造有限公司，黑龙江哈尔滨150078;②哈尔滨工业大学，黑龙江哈尔滨150001;③郑州职业技术学院，河南郑州 450121）

目前，风力发电多采用升力型水平轴风力机［1］。该类风力发电机组中的增速箱机构、偏航机构、变桨机构均需大规格齿轮。此类齿轮齿形根据其精度要求及齿轮形式，采用不同的加工工艺，一般来讲，对于5～6级的内齿齿轮或外齿齿轮采用铣齿后磨齿;对于8～9级的外齿齿轮采用铣齿后滚齿;对于8～9级的内齿直齿轮采用铣齿后插齿。铣齿现在主要是采用高速铣齿机利用硬质合金可转位盘形铣刀进行齿轮的成形铣削加工，使齿轮的粗加工、半精加工的效率极大的提高。但目前采用的可转位盘形铣刀多为刀片搭接形式，如图1所示，以多片直线刀片为一组，逼近渐开线齿形。此种方式，刀片数量多，刀片之间的搭接凹痕无法消除。精切齿轮铣刀是采用一个刀片形成渐开线齿形，如图2所示。刀片数量减少，形线准确，无刀片搭接痕迹，一次加工渐开线齿形成形，可达到IT9级精度［2］。鉴于精切齿轮铣刀的优点，其应用已逐渐成为一种趋势，特别是用于内齿轮的加工，可部分替代插齿加工。精切齿轮铣刀设计关键在于刀片切削刃廓形的设计，既要使刀片便于加工，又要保证其加工出的渐开线齿形的精度满足要求。

1 刀片切削刃廓形求解方法

图3是一种立装结构的内齿轮精铣刀的刀片廓形，切削刃由曲线AB、BC组成，曲线AB段切削刃加工齿根过渡圆弧和齿根直线部分;曲线BC段切削刃加工有效渐开线部分。由于曲线AB段切削刃加工部位不影响内齿圈精度，其廓形只要能满足加工出圆角及直线部分即可，所以不做讨论，主要讨论曲线BC段切削刃的廓形的形成。

从图3中可以看出刀片为矩形。该刀片要安装在铣刀上时，需转一个角度才能形成切削后角，与此同时形成负的切削前角，此时的切削刃已与铣刀的轴截面廓形不同，因此需对其进行修正计算，为了便于分析计算，将刃形简化处理，如图4所示。

铣刀轴向截面廓形上一点a在G点位置旋转θ角后落在刀片上E点，即是铣刀前刀面切削刃的实际廓形上的一点。则有:

从图4中的△OAE存在的三角函数关系，可以推导出:

所以铣刀的前刀面切削刃的廓形坐标方程为:

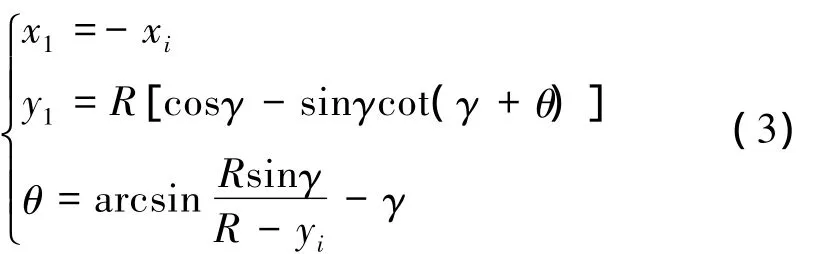
式中:R为铣刀外圆半径;γ为齿铣刀切削前角;xi、yi为铣刀轴截面廓形上的已知坐标点。

通过式（3）计算出的铣刀前刀面切削刃的廓形坐标即是设计刀片切削刃廓形的坐标（刀片还要转一个法向后角，但为了简化设计，不再进一步求解转后角的切削刃廓形坐标，由此产生的切削刃廓形误差在后面进行分析）。

2 刀片切削刃的拟合

前面计算出的刀片切削刃的廓形坐标为数值点，磨制时需逐点给出坐标值，程序编制难度大，测量和检验也较困难。为了方便刀片的制造、测量和检验，则用一段圆弧代替计算出的理论廓形，这里采用最小二乘法进行计算［3］。设所求出的刀片切削刃的廓形上一系列点的坐标值为Mi（xi，yi），i=0、1、2、3、…、n。设要用来代替的圆弧半径为R，圆心坐标为 （xa，ya），则它的方程式为

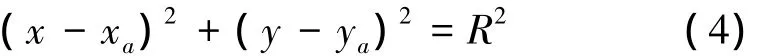
式（4）中的xa、ya、R均是待定参数。将该公式展开整理得:

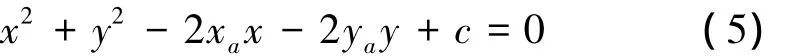
其中

当用理论上一些点的坐标值（xi，yi）代入式（5）时会存在一个偏差值。而最小二乘法是采用偏差平方和为最小的方法，同样可以确定系数xa、ya、c，以使各点的偏差值都最小，将此时求得的xa、ya、c，作为代用圆弧的圆心坐标和半径。即有如下方程成立:

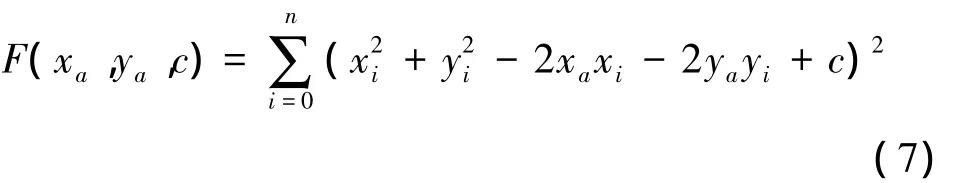
运用求极值的方法，由∂F/∂xa=0、∂F/∂ya=0、∂F/∂c=0，得到如下方程:

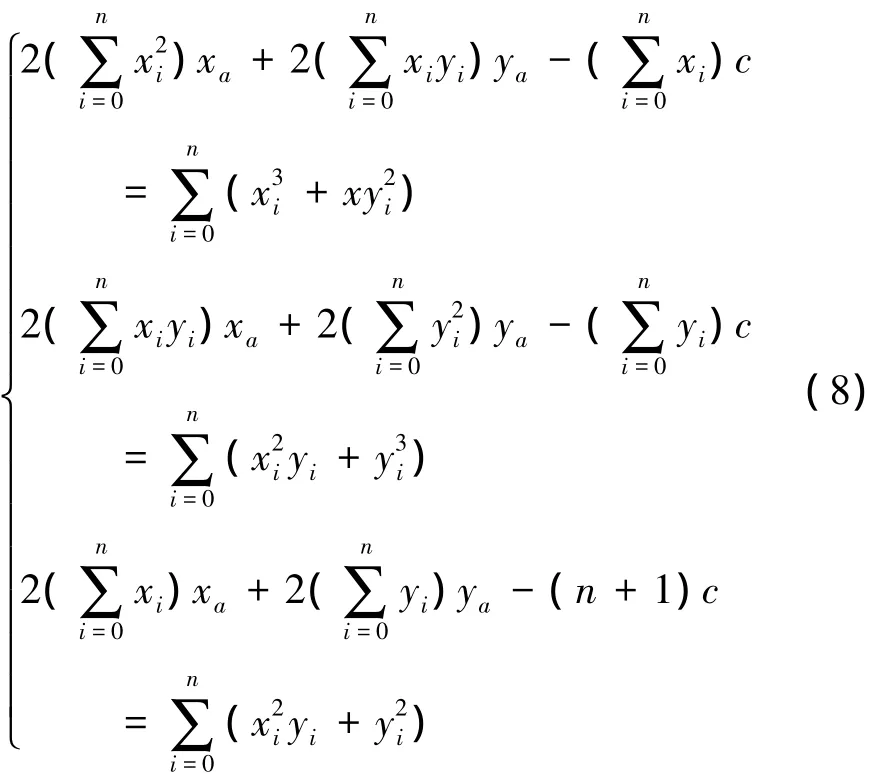
式（8）是一个三元线性方程组，可根据已知的xi，yi，计算出xa、ya、c，则代用圆弧半径R可由下式求出:

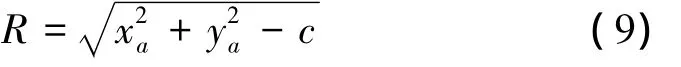
3 刀片刃形误差对齿轮加工精度的影响分析

刀片切削刃型在设计时采取的一些简便方法、铣刀加工齿轮过程中刀片后刀面磨损等方面都会对齿轮的加工精度造成一定影响，这里对产生误差的原因及对齿轮精度的影响程度进行简要分析。假设工件模数为m12 mm、分度圆为1 300 mm左右的9级精度齿轮，因此误差应小于该齿轮规定的齿廓总偏差规定的0.08 mm 的要求范围［4］。

3.1 刀片切削刃拟合误差产生的影响

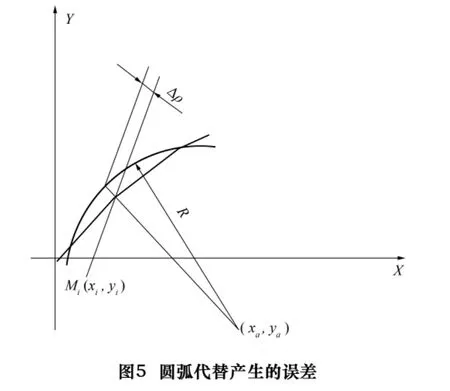
在前面对切削刃的拟合采用最小二乘法用圆弧代替理论刃形，如图5所示。采用该方法时，沿圆弧半径R方向会存在一个误差Δρ，即理论齿形坐标Mi（xi，yi）的齿形误差为

利用式（10），将已求出的刀片刃形坐标及拟合的圆弧参数逐一代入，计算的结果远远小于齿轮9级精度规定的齿形误差要求，因此该误差可忽略不计。

3.2 刀片切削刃后角误差产生的影响

前面提到铣刀在设计时，刀刃需转一个法向后角，通常转4°～6°，转后角后铣刀的切削刃由圆形变成的投影实际应是椭圆［5］，如图6所示（为了表示清楚，该图为夸大画法），刀片刃口绕xx'轴旋转，变化量最大的为B点，即该点变为C点，验证该点变化量是否超差即可。该点由于刀片刃形为该圆的一段弧，其弧经过转角后，变化的距离BC为

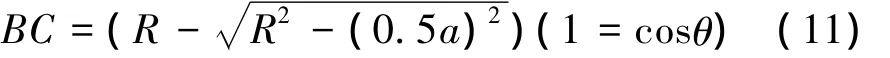
式中:R为圆弧半径;a为刀片长度;θ为刀片旋转的法向后角。经过计算，其变化量在0.001 mm左右，也远远小于齿轮9级精度规定的齿形误差要求，因此该误差也可忽略不计。

3.3 刀片切削刃磨损误差产生的影响

如图7，铣刀加工齿轮工件时主要是后刀面磨损，其磨损程度用B区比较均匀的平均宽度VB衡量［6］。

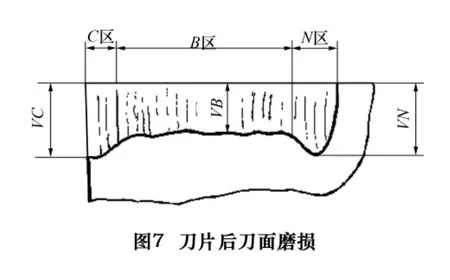
通过检测VB值即可间接计算出由于磨损导致刀片刃口线形发生变化，变化值Δ可按式（12）计算，其中θ为刀刃的法向后角:

当Δ按最大值取0.08 mm、θ取4°计算时，VB为1.14 mm。另外，硬质合金盘铣刀加工钢件时的VB值通常为0.3～0.5 mm［8］，即当刀片磨损达到极限最大值时的Δ值不大于0.035 mm，因此，当刀片到达磨损极限时，将刀片转位就不会对齿形误差造成影响。

从以上三个方面分析可以看出，上述三种因素引起的精度问题累计起来对齿形误差的影响远远小于规定的要求。

4 结语

笔者通过一些简便算法设计精切刀片的切削刃廓形，简化了刀片的磨制程序，也方便了检测，为今后类似刀片的设计提供了一种新思路，通过分析，此方法设计出的刃形能够满足要求，并在实践中得以验证。但文中只是对刀片刃形误差对齿轮精度的影响进行了简要分析，实际生产时影响齿轮精度的原因有很多，比如刀具制造精度、刀具切削时的受力变形和切削热引起的变形等等，在此未作分析。

［1］熊礼俭.风力发电新技术与发电工程设计、运行、维护及标准规范实用手册［M］.中国科技文化出版社，2005.

［2］Kennametal.Gear cutting tools［Z］.Kennametal，2009.

［3］刘杰华.刀具精确设计理论与实践［M］.北京:国防工业出版社，2005.

［4］齿轮手册编委会.齿轮手册［M］.北京:机械工业出版社，2001.

［5］王可，呼咏，陈欣，等.无瞬心包络法加工螺杆的精度分析［J］.组合机床与自动化加工技术，1999（1）.

［6］陈日耀.金属切削原理［M］.北京:机械工业出版社，2005.

［7］艾兴，肖诗刚.切削用量手册［M］.北京:机械工业出版社，1985.