伺服电动机的振动抑制*

黄 宾 马 跃 田军锋

（中国科学院沈阳计算技术研究所，辽宁沈阳 110168）

随着伺服驱动技术的发展，伺服系统广泛应用于工业机器人、数控机床等，工业机器人以及数控机床的先进性取决于加工精度，而伺服电动机在驱动机械时，机械的刚性与结构、间隙、轴中心的偏移等都会引起电动机振动，电动机振动导致设备精度降低，如果工业机器人和数控机床精度受电动机振动的影响，将影响被加工装备的质量，就这一角度而言，电动机振动抑制的研究十分必要。电动机的振动抑制是电动机控制领域的一个重要分支，电动机振动抑制的研究对促进电动机控制也有着重要意义。以振动抑制为目的的控制技术研究飞速发展，对因机械系统刚性低而引起的扭转振动的研究尤其广泛，提出了诸多解决方案。采用传统PID控制是过去50年常用的方法，随后出现了利用观测器、陷波器、滤波器结合PID控制的控制方法对传统的PID控制进行改进，发展至今又提出了与自适应算法、模糊控制理论、滑模变结构、H∞控制理论、神经网络以及遗传算法等结合的控制方法，还有加入快速傅里叶变换（FFT）的补偿方法。另外，19世纪60年代早期提出的一种分析系统动态性的方法——状态空间方法论，最近几年才开始在工业上应用，近几年又提出了一种具有很高的抑制响应非线性的控制方法。

电动机振动分为机械振动和电磁振动，扭转振动和转矩脉动是机械振动和电磁振动的两种典型振动，许多学者对其进行了研究。本文总结了大量近5年内的文献以及少量5年前的文献，重点分析了抑制扭转振动和转矩脉动的方法，对文献中提出的同类或类似方法进行纵向对比，找出方法之间的区别和适用对象，对同类型振动的抑制方法在系统复杂度、动态性、鲁棒性以及其他特性方面进行横向比较，以此来了解各种振动抑制方法的优劣性，并对振动抑制方法的发展进行展望。

1 扭转振动抑制方法

扭转振动普遍存在于双质量系统（Double Mass System）或双惯性系统（Double Inertia System），扭转振动的存在影响着系统的精度，针对扭转振动的抑制，许多学者对其进行了研究，得出很多抑制扭转振动的控制方法，如基于PID的控制、基于观测器的控制、基于滤波器和陷波器的控制、H∞控制、共振比率控制和智能控制等。振动抑制方法发展至今，形成了多种方法结合的复合控制方法。

1.1 典型的扭转振动抑制复合方法分析

由于单独采用某种控制策略来抑制扭转振动有着各自的缺陷，如单独采用PID控制，当输入改变时，PID参数需重新整定，自适应差;又如单独采用陷波器智能对高频振动的抑制有效果。为了完善振动抑制方法，使其具有自适应性、鲁棒性等特点，多种振动抑制方法之间复合形成的控制方法能有效地达到这一目的，但与此同时也产生了新的问题，下面将对几种比较典型的复合控制方法进行分析。

1.1.1 基于观测器的复合振动抑制方法

双惯性系统中反共振频率与共振频率的比值与惯性比有关，该比值对振动抑制控制的性能将产生很大的影响。Liangsong Huang等人在此基础上提出了一种基于扰动观测器设计的可调节惯性比控制策略［1］，通过把惯性比调节到一个优化的比率达到抑制扭转振动的目的。该方法简单易行，系统复杂程度不高，能使伺服系统平滑稳定地工作。但是该方法在对公式进行变形的过程中做了大量假设，假设是否合理尚有待商榷，在假设成立的前提下，系统的可扩展性较低。

Wen Li提出了一种用分数阶扰动观测器和基于神经元的PI模糊控制器来实现双惯性系统中的振动抑制的方法［2］，分数阶扰动观测器用于获得扰动估计和产生补偿信号，基于神经元的PI模糊控制器则用来实现外环控制。用分数阶扰动观测器的好处是，由于引进分数计算使Q滤波器从整数域扩展到实数域，使得系统在适当的鲁棒性和振动抑制两者中有更宽的折衷范围，增强了系统的鲁棒性。

1.1.2 基于陷波器的复合振动抑制方法

滤波器、陷波器在双惯性系统的振动抑制方面充当着重要角色。吕金等人提出了一种在PI控制器中加入陷波滤波器的方法［3］，通过陷波滤波器将速度中的谐波分量过滤，达到抑制扭转振动的效果。

Stone Cheng等采用自适应陷波器提出了一种改善了的速度控制环的带宽的方法［4］，该结构基于自适应IIR陷波器技术的控制结构，解决了采用自适应IIR陷波器方法只能消除高频振动和计算量大的缺点，使其能应用于低频振动的抑制。

自适应陷波器能够自动识别振动频率，自动调节陷波器的参数，从而达到自动抑制的目的，具有很强的自适应性。

1.1.3 基于H∞控制理论的复合控制方法分析

基于H∞控制理论设计的控制器能在摄动时保持系统的特性，H∞控制器的这一优点使其在振动抑制领域广泛应用。如Shigeo Morimoto等提出了一种基于H∞控制器的双自由度控制器的设计［5］用来改善速度命令的轨迹特性。高阶的H∞控制器能够应用于实际系统，该方法跟传统的PI速度控制相比在鲁棒性和动态响应上有显著提高，且能够有效地抑制扭矩转动和扰动。

Jian FU设计了一种观测器和H∞滤波器结合的系统［6］，提出了一种 CCHFLO（Compensative Control Based On H∞ Filter and Load Observer）的控制方法。该方法振动能够得到很好的抑制且具有鲁棒性，缺点是系统比较复杂。

Teresa Orlowska－Kowalska和 Krzysztof Szabat提出了另一种H∞控制理论与神经模糊结合的控制方法［7］，该方法采用自适应神经模糊滑动速度控制，能够很好地抑制扭转振动，系统参数的范围很广，鲁棒性强且系统的动态响应好。

另外，Jianhui Wang等提出了一种根据最优控制理论提出了一种新的预测控制模型［8］。该模型能够使系统的动态响应接近参考输入，且系统动态曲线平滑，但是作者采用的参考输入很小，适用范围很小，有待提高。同样利用预测模型的方法有牛志刚等提出的利用Turbo PMAC运动控制器的超前观测功能来实现振动抑制［9］。超前预测的实质是一种变插补周期的控制方式，不依赖于具体机构的运动学模型。

1.2 扭转振动抑制方法比较

综上所述，传统的PI控制系统相对简单，但对减小振动效果不明显，在利用PID控制的过程中，一旦参数整定，就不能改变，鲁棒性较差;滤波器和陷波器能抑制高频振动，自动识别振动频率，自动调节参数，具有极强的自适应性和鲁棒性，但是对系统的动态性影响较大;共振比率控制（RRC）在共振频率/反共振频率值很大时拥有良好的抑制能力。智能控制方法系统复杂但是具有很好的自适应性和鲁棒性;H∞控制能有效地控制系统的鲁棒性，但是该方法以牺牲系统的动态性为代价。几种主要扭转振动抑制方法在系统复杂度、动态性、自适应性和鲁棒性上比较结果如表1所示。

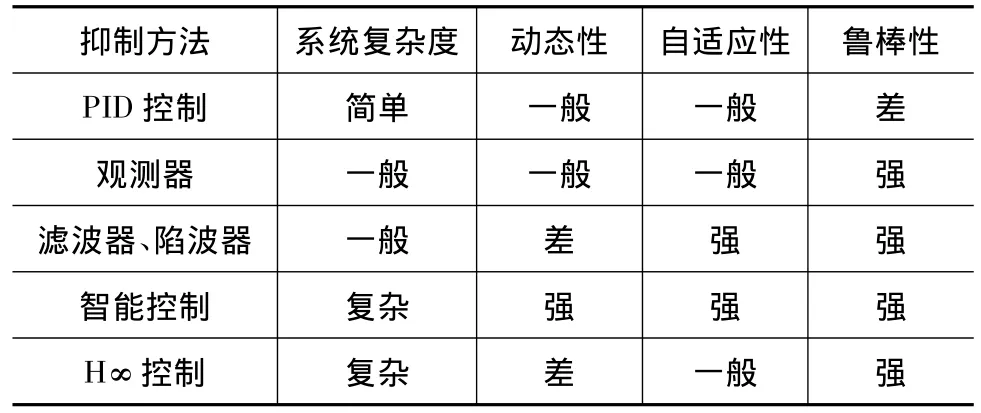
表1 扭转振动抑制方法比较

2 转矩脉动抑制方法

转矩脉动（Torque Ripple）也叫转矩波动、转矩振动（Tourque Vibration），是由转矩时大时小引起的振动。根据转矩脉动产生的机理不同，采用的转矩脉动抑制的方法主要有如下两种:一种是电动机本体的优化设计，通过气隙磁场，定转子结构，绕组形式等的合理设计来消除齿槽转矩，使反电动势波形接近理想波形;另一种是从控制策略入手，通过调整加在定子绕组上的电压或电流波形来抑制转矩脉动［10］。比较典型的抑制转矩脉动的方法有:谐波消除法、直接转矩控制和智能方法等。

2.1 典型转矩脉动抑制方法分析

2.1.1 谐波消除法

电流中谐波使电流波形变形，谐波的存在会引起谐振，对电动机振动影响很大。谐波消除法主要是对电流中的主要谐波进行补偿，达到消除谐波从而减小振动的目的。针对非正弦反电动势和锯齿波导致的永磁同步电动机扭转振动Damien J.Hill等人提出了一种在扭矩和传感器输入之间利用任何传感器的线性传递函数的控制方法［11］。该方法属于转矩波动补偿的迭代方法，使用该方法转矩在幅度上的变化低于2%，关键的转矩谐波至少减少了1/3，但是该方法只对20和24次谐波进行了补偿。从文中的分析中可以看出，10次和50次谐波对转矩振动的影响也较大，因此，该方法还可以进一步改进，对10次和50次谐波进行谐波补偿。

廖勇等人提出了一种谐波注入的方法在PMW三相调制参考电压波形中加入相应的谐波分量来抵消电动机电流中的谐波［12］。该方法和上述方法不同之处在于选择的谐波次数不同，该方法选择5、7次谐波进行消除。作者通过分析发现5、7、11、13等次谐波对永磁电动机的影响较大，因此选择了前两次谐波加以补偿。该方法与文献［11］中提出的谐波补偿次数有区别，原因可能与电动机型号有关。该方法具有与Damien J.Hill提出的方法相同的缺陷，仍可继续对11和13次谐波进行补偿，从仿真结果来看，Damien J.Hill的仿真结果比廖勇的要好，且与传感器类型无关。

Jin－Wook Reu 等提出类似的方法［13］，该方法通过IPM电动机空隙磁通密度散布情况来消除负三次谐波以实现振动最小化的方法。该方法利用有限元方法来计算振动的变化，分析扭转振动源，结合加速度传感器来实现振动的抑制。

2.1.2 直接转矩控制（DTC）

直接转矩控制（DTC）采取定子磁链定向，利用两点式进行调节直接对电动机的磁链和转矩进行控制，使电动机转矩迅速响应。直接转矩控制方法最早是针对感应电动机提出的。直接转矩控制是采用磁链定向和空间矢量概念，通过检测定子电压、电流，直接在定子坐标系下观测电动机的磁链、转矩并将此观测值与给定磁链、转矩相比，差值经两个滞环控制器得到响应的控制信号再综合当前磁链状态从开关表中选择合适的电压空间向量来控制逆变器的电子开关的状态，直接对电动机转矩实施控制［14］。

周永勤提出了一种基于转矩分配的模糊PI控制器的方法［15］来实现参数在线优化调整的方法。该方法采用一种综合控制策略，用双闭环控制，外环为速度控制，用模糊PI控制器;内环为转矩跟踪控制。方法能够提高系统动态响应，具有良好的动静态性能，并抑制转矩脉动，且应用到了实际工程，可供别的系统借鉴。

滑模结构在自控领域的应用越来越广，在转矩脉动控制中也得以应用。杨俊华提出了一种引进滑模变结构的控制策略［16］，用转矩和磁链两个滑模控制器代替了传统直接转矩控制中的两个滞环控制器。该方法能减小转矩脉动，改善定子磁链和电流波形，在保持直接转矩控制固有的转矩快速响应优点的同时提高了系统的稳定性，且具有鲁棒性，但是该方法对系统的控制状态要求频繁、快速的切换。同样具有滑模变结构的方法有马宪民根据变结构控制理论提出的采用滑模－PI变结构的控制策略［17］，该策略有助于克服非线性因数对系统的影响，减小了转矩脉动，降低了噪声并且提高了系统的鲁棒性。

2.1.3 智能控制及其他方法

一些智能方法也应用于转矩控制，比如模糊算法［18－19］、神经网络［20］和迭代算法［21］、遗传算法［22］等。采用模糊算法的系统能够减少电动机的转矩和磁通脉动［18］，抑制转矩脉动系数［19］;单神经元构成的控制器［20］相对于神经网络来说结构简单，计算量少，易于计算机实现，具有在线自学习能力，具有自适应能力，对扰动的鲁棒性好;迭代学习控制算法简单，在控制过程中不需要预知被控系统模型和参数的特点，具有记忆和修正机制，对系统参数依赖性低，抗干扰性好。由此可见，智能算法普遍具有抗干扰性，自适应和鲁棒性。

另外还有PTC（Perfect Tracking Control，完善的跟踪控制）法［23］，无涟波转矩控制方法［24］，利用傅里叶变换［25－28］的迭代控制。PTC方法把转矩脉动用关于转子角度的函数表示，最终把转矩脉动的抑制问题转化成了速度控制的问题，方法实用且能在速度变化的同时不必调节参数，具有很好的自适应能力和鲁棒性。无涟波转矩控制方法对包括了3相不平衡情况的相电流进行了优化，能获得优化的电动机激励电流，该方法也可以认为是另一种谐波电流注入法，相对简单明了，不用考虑相位变化，对反电动势的形状、量级和半波对称等没有特殊要求。采用傅里叶变换的迭代方法补偿信号能在线获得，可适用于不同电动机，具有自适应性，鲁棒性强，但是该方法的缺点是计算量大，且相电压和d/q轴电流较其他控制方法波动大。

2.2 转矩脉动抑制方法比较

综上所述，谐波注入法跟其他方法相比，针对性较强，能很好地消除特定型号电动机的转矩脉动，系统结构较简单，计算量较大，鲁棒性最差;直接转矩控制法，响应迅速，是基本的消除转矩脉动的方法，可以和其他方法复合控制;智能算法自适应性好，抗干扰能力强，因此鲁棒性强，计算量最大。几种主要转矩脉动抑制方法在系统复杂度、计算量、自适应性和鲁棒性上比较结果如表2所示。

表2 转矩脉动抑制方法比较

3 总结与展望

本文大量总结了近几年关于振动抑制方法的文献，具有较强的时效性。将针对不同类型振动所提出的振动抑制方法进行了分析和总结，从横向和纵向对不同方法的不同特性加以对比，且以图表的形式呈现，方法的优劣性对比直观，一目了然。

振动抑制经过多年的发展，从传统的PID控制方法到结合了人工智能方法的控制方法的出现，完善了各种抑制方法中的鲁棒性、自适应性等问题，使整个控制系统具有良好的自适应性和强鲁棒性等优点，已经日趋完善，但仍有一些问题亟待解决:（1）结合了人工智能算法的控制方法计算量大，复杂的计算势必影响系统的响应。结合以上对扭转振动和转矩脉动等抑制方法的分析，把振动抑制的方法加以改进使其具有快速响应的特点，使振动抑制方法能应用于更广泛的领域，让电动机传动系统朝着高速高精的目标发展。（2）产生振动的原因很多，导致振动类型多样化，系统中可能包含一种以上类型的振动，如果只针对某种振动进行抑制，对其余类型的振动抑制效果可能并不明显，因此，找出一种抑制由多原因引起的振动的方法有其必要性。

［1］Huang Liangsong，Qu DaoKui，Xu Fang.Adjustable inertia ratio control for low－frequency torsional resonance suppression in industrial servo system［C］.2010 International Conference on Measuring Technology and Mechatronics Automation，2010:432－435.

［2］Wen Li，Yoichi Hori.Vibration suppression using single neuron－based pi fuzzy controller and fractional– order disturbance observer［J］.IEEE Transactions On Industrial Electronics，2007，54（1）:432－435.

［3］吕金，朱传磊，周本川.陷波滤波抑制轧机扭振［J］.电气传动，2008，38（6）.

［4］Shiang Chih Fu，Seung– Ki Sul.Analysis and suppression of torsional vibrations for the permanent magnet synchronous motor－load system［C］.Proceedings of the 2009 IEEE International Conference on Systems，Man ，and Cybernetics San Antonio，TX，USA，2009:3359－3364.

［5］Shigeo Morimoto，Masakazu Ohashi，Yoji Takeda，et al.High performance speed control for torsional system based on H∞ control theory［C］.Power Electronics and Drive Systems，Proceedings of 1995 International Conference，1995:828－833.

［6］Fu Jian，Yang Weidong，LI Boqun，et al.H∞ filter and load observer based compensative control for vibration suppression of rolling mill［C］.Proceedings of the 6th World Congress on Intelligent Control and Automation，Dalian，China，2006:2209－2213.

［7］Teresa Orlowska－Kowalska，Krzysztof Szabat.Damping of torsional vibrations in two－mass system using adaptive sliding neuro－fuzzy approach［J］.IEEE Transactions On Industrial Informatics，2008，4（1）.

［8］Wang Jianhui，Zhang Yuxian，Xu Lin，et al.Torsional vibration suppression of rolling mill with constrained model predictive control［C］.Proceedings of the 6th World Congress on Intelligent Control and Automation，Dalian，China，2006:6401－6405.

［9］牛志刚，张建民.并联机构实轴伺服电机的振动抑制［J］.机械工程，2005，16（23）.

［10］任军军.永磁无刷直流电机的转矩脉动抑制的控制策略研究［D］.杭州:浙江大学，2004.

［11］Hill Damien J，Greg Heins，Friso de Boer.Tourque ripple estimation and minimisation independent of sensor type［C］.2011 IEEE International Electric Machines＆ Drives Conference，2011:463－468.

［12］廖勇，甄帅，刘刃，等.用谐波注入抑制永磁同步电机转矩脉动［J］.中国电机工程学报，2011，31（21）.

［13］Jin－Wook Reu，Jin－Hur，Byeong－Woo Kim，et al.The novel method for vibration reduction of ipm type bldc motor［C］.Electromagnetic Field Computation（CEFC），14th Biennial IEEE Conference，2010.

［14］苏陈云，杨向宇.永磁同步电机直接转矩控制转矩脉动的产生及其抑制方法综述［J］.微电机，2010（3）.

［15］周永勤，姜云峰，徐海伟.基于转矩分配的开关词组电机模糊PI控制系统［J］.自动化技术与应用，2010，29（6）.

［16］杨俊华，刘远涛，谢景凤，等.无刷双馈电机滑模变结构直接转矩控制［J］.微电机，2010（3）.

［17］马宪民.滑模－PI变结构控制开关词组电动机调速系统的研究［J］.电气自动化，2002（1）.

［18］高圣伟，汪友华，蔡燕，等.基于模糊逻辑的DTC减小转矩脉动方法研究［J］.河北工业大学学报，2011，40（3）.

［19］张海军，张京军，高瑞贞，等.基于有限元模型的SRM相电流模糊补偿控制［J］.电气自动化，2002（1）.

［20］李莺，蒋泽甫，罗毅，等.基于神经元和直接转矩控制技术的高性能交流调速系统研究［J］.重庆邮电大学学报:自然科学版，2010，22（1）.

［21］潘再平，罗星宝.基于迭代学习控制的开关磁阻电机转矩脉动抑制［J］.电工技术学报，2010，25（7）.

［22］Takeshi Miura，Toshiyuki Taniguchi.A new approach for minimumtorque－ripple maximum－efficiency control of bldc motor［J］.IEEE Transactions On Industrial Electronics，1999，46（6）:1192－1194.

［23］Kento Nakamura，Hiroshi Fujimoto，Masami Fujitsuna.Torque ripple suppression control for pm motor with current control based on PTC［C］.International Power Electronics Conference，2010:1077－1082.

［24］Sung Jun Park，Han Woong Park，Man Hyung Lee，et al.A new approach for minimum－torque－ripple maximum－efficiency control of BLDC motor［J］.IEEE Trasactions On Industrial Electronics，2000，47（1）.

［25］Satomi Hattori，Muneaki Ishia，Takamasa Hori.Vibration Suppression Control Method for PMSM Utilizing Repetitive Control with Auto－tuning Function and Fourier Transform［C］.IECON’01:The 27th Annual Conference of the IEEE Industrial Electronics Society，2001:1673－1679.

［26］Kenji Kawai，Tadanao Zanma，Uneaki Ishida.Simultaneous vibration suppression control of PMSM using repetitive control with Fourier series［C］.Industrial Technology，ICIT 2006.IEEE International Conference ，2006:854－859.

［27］Tinghsu Su，Muneaki Ishia，Takamasa Hori.Suppression control method for torque vibration of 3－phase HB－type stepping motor utilizing feedforward control［C］.Industrial Electronics Society，IECON 2000:The 26th Annual Confjerence of the IEEE，2000:1093－1098.

［28］Tinghsu Su，Satomi Hattori，Muneaki Ishia，et al.Suppression control method for torque vibration of AC motor utilizing feedforward control［J］.IEEE Transactions On Industry Applications，2002，38（5）:1093－1098.