投标者为风险规避型引入佣金的分析（一）

肖海燕

（湖北第二师范学院数学与数量经济学院，湖北 武汉 430205）

拍卖这种交易方式有着悠久的历史。古往今来，被拍卖的物品也形形色色，从古玩字画到日常用品，从农产品到海鲜、政府债券、营业执照和电波频率等各种有形无形的商品无所不包。最近几年，拍卖被用来出售政府资产、电信执照以及电力市场的产品，引起了人们的关注。因特网和电子商务的发展，使得网络拍卖也日渐兴盛，不但出现了专业的拍卖网站，许多交易也采用拍卖的方式。从广义上理解，拍卖是市场经济价格均衡机制及资源配置的内在过程和本质机理；从狭义上理解，拍卖是有一定适用范围及特殊规定的一种重要的国际贸易形式。

拍卖理论的研究在国外已经发展到成熟的阶段。1961年VICKREY［1］提出了独立私有价值下的基本拍卖模型，发现密封一价拍卖和密封二价拍卖下的期望收益相同。1981年RILEY和SAMUELSON［2］对对称独立私有价值模型做了详细分析，得出了收益等价性定理，并说明VICKREY的结论具有一般性。这两篇文章成为随后其他学者研究拍卖理论的奠基石。1976年VICKREY提出了对4种基本拍卖模型的划分，在基本模型框架内对竞买者行为进行了详细的探讨。随后，研究者逐渐放松基本模型内各种假设，包括风险规避、竞买者不对称、全支付拍卖［3］、竞买者信息相互影响和竞买者进入成本等，如MILGROM和WEBER［4］在竞买者信息相互影响下得出一定的序关系，并对保留价和入场费的引入进行了讨论。VIJAY［5］讨论了一价全支付拍卖和二价全支付拍卖，并对一价拍卖、二价拍卖、一价全支付拍卖和二价全支付拍卖4种形式进行了收益比较，得出一定的序关系。后来许多学者在有效性［6］、非对称［7］、共谋环［8］、多物品拍卖［9－10］、多属性拍卖［11－12］和序贯拍卖［13］领域做了许多工作。

在实际拍卖操作中卖方往往需要委托第三方（拍卖行）对物品进行拍卖，拍卖行对成交的拍卖品收取佣金，一般由中标者支付。李寿德等［14］建立了基于预算与佣金约束的排污权关联价值拍卖模型；王彦等［15］考虑了在风险中性下，佣金收取对拍卖结果的影响。实际上风险中性是当风险规避型效用函数u（x）=x时的一种特殊情况，因此笔者在此基础上考虑在投标者为风险规避型的对称独立私有价值（SIPV）模型下，佣金收取对拍卖结果的影响。

1 密封二价拍卖

设拍卖方拍卖一个不可分割的物品，有N个买方对该物品感兴趣，并假设每个投标者都为风险规避型，具有相同的效用函数u（x），满足u（0）=0，u'＞0，u″＜0，且对该物品的估值为 Xi，i=1，2，…，N。对于买方来说，只有他自己知道Xi的大小，卖方及其他买方都不知道，但他们会认为Xi是［0，ω］上的概率分布函数 Fi（xi），密度函数fi（xi）为随机变量。现假设所有投标者是对称的，即∀x∈［0，ω］，Fi（x）=Fj（x）=F（x），i=1，2，…，N，j=1，2，…，N，拍卖行按成交价的某个比例k收取佣金。以上所有假设对于买方、卖方及拍卖行来说是共识。

在私人估价为Xi的情况下，投标者策略出价bi使其期望效用最大，由于各投标者私人信息各不相同，从而估价各不相同，每个投标者会把对方的出价策略视为一个函数 βj（xj），xj∈［0，ω］，由对称性可知，∀x∈［0，ω］，βi（x）=βj（x）=β（x）。该博弈问题的均衡解为策略{β*（x1），β*（x2），…，β*（xN）}，使得每个投标者i在其他人的出价为β*（xj）时出价β*（xi）为最优。一般情况下，均假设β（x）是单调递增的。

由对称性，考虑投标者1，Y1=Xj为除第1个投标者以外的其余N－1个投标者估值中的最大者，则随机变量Y1的分布函数为G（x）=F（x）N－1，密度函数为 g（x）=G'（x）。投标者 1的私人估价为x，报价为β（z）的期望效用为:

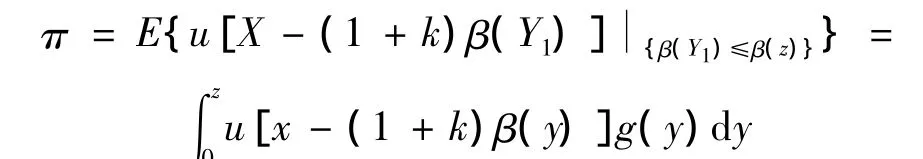
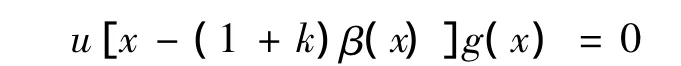
即 u［x－（1+k）β（x）］=0，由 u（0）=0，且u'＞0，可推出:

（1）卖方的期望收益为:

式中:e（X）为SPIV模型二价拍卖机制下的期望支付；Y（N）2为私人估值X1，X2，…，XN的第二高值。

（2）拍卖行的期望收益为:

（3）投标者的期望效用为:

由式（1）～式（4）可得两个结果。

（1）SIPV模型下，投标者的均衡出价随着佣金比例k的提高而减少，但是其期望效用与k无关；卖方的期望收益随着佣金比例k的增加而降低；拍卖行的期望收益随着k的增加而增加。

（2）SIPV模型下，由于需支付一定比例的佣金，投标者出价会更谨慎；从期望收益的角度来看，投标者并没有因为佣金支付减少期望效用，而是卖方的期望收益减少了，减少的部分正好是拍卖行获得的期望收益。

2 密封一价拍卖

同样地，考虑投标者1，私人估价为x，报价为α［z］，其期望效用为:

π =G（z）u［x － （1+k）α（z）］由于在对称均衡处必有z=x，从而有必要条件=0，即:

令 B（x）=（1+k）α（x），则式（6）变为:

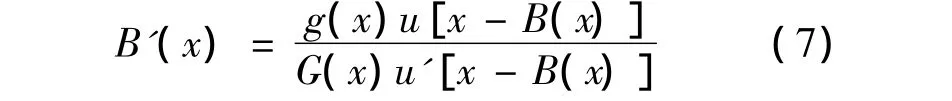
可以看出式（7）的解B（x）与k无关，且容易证明B（x）正好是SPIV模型下无佣金提成时的均衡出价。

（1）卖方的期望收益为:

（2）拍卖行的期望收益为:

（3）投标者的期望效用为:

3 结论

在投标者为风险规避型的情况下，将佣金提成引入拍卖理论中，在对称独立私有价值情况下进行讨论，可以得出以下结论:佣金比例k越高，则投标者报价越低，卖方的期望收益越少，拍卖行的期望收益越大，投标者的期望效用与k无关。

因此在实际拍卖中，投标者不用为佣金比例的高低担心，佣金比例越高，投标人对物品的评价会降低，最后付给卖方的价格也会降低。投标者为风险规避型情况下，有待进一步研究的问题是:①在独立私有价值佣金收取模型下，一价、二价拍卖期望收益比较；②在关联价值模型下佣金收取对拍卖的影响。

［1］VICKREY W.Counterspeculation，auctions and competitive sealed tenders［J］.Journal of Finance，1961（16）:8－37.

［2］RILEY J G，SAMUELSON W F.Optimal auctions［J］.American Economic Review，1981（71）:381 －392.

［3］王先甲，陈文磊.全支付拍卖模型的信息结构及其对均衡的影响分析［J］.数学物理学报，2010，30A（5）:1276－1282.

［4］MILGROM P R，WEBER R J.A theory of auctions and competitive bidding［J］.Econometrica，1982，50（5）:1089－1122.

［5］VIJAY K，JOHN M.An analysis of the war of attrition and the all－ pay auction［J］.Journal of Economic，1997（72）:343－362.

［6］DASGUPTA P，MASKIN E.Efficient auctions［J］.Quarterly Journal of Economics，2000（115）:341 － 388.

［7］MASKIN E，RILEY J.Asymmetric auctions［J］.Review of Economic Studies，2000（67）:413 －438.

［8］MCAFEE P，MCMILLAN J.Bidding rings［J］.American Economic Review，1992（82）:579 －599.

［9］ARMSTRONG M.Optimal multi－ object auctions［J］.Review of Economic Studies，2000（67）:455 －481.

［10］MANELLI A M，SEFTON M，WILNER B S.Multiunit auctions:a comparison of static and dynamic mechanisms［J］.Journal of Economic Behavior and Organization，2006（61）:304 －323.

［11］BIEHLER M.An experimental analysis of multi－ attribute auction［J］.Decision Support Systems，2000（29）:249－268.

［12］孙亚辉，冯玉强.多属性密封拍卖模型及最优投标策略［J］.系统工程理论与实践，2010，30（7）:1185－ 1189.

［13］SALMON T C，WILSON B J.Second chance offers versus sequential auctions:theory and behavior［J］.Economic Theory，2008（34）:47 －67.

［14］李寿德，黄采金，顾孟迪，等.基于预算与佣金约束的排污权关联价值拍卖机制［J］.系统管理学报，2008，17（1）:56 －59.

［15］王彦，毕志伟，李楚霖.佣金收取对拍卖结果的影响［J］.管理科学学报，2004，7（4）:45－49.