一维离散系统的混沌及其控制

高智中

一维离散系统的混沌及其控制

高智中

（安徽科技学院理学院，安徽，凤阳 233100）

详细研究一类一维离散系统的动力学行为，重点分析了该系统由周期运动到混沌运动的转迁过程，并根据其转迁特点设计了一种混沌控制方案，数值仿真结果表明我们的控制方案能够有效控制该系统的混沌状态。

分岔图；Lyapunov指数图；混沌；混沌控制

由于混沌信号对初值极端敏感、互不相关、有界等特点，所以在混沌保密通讯中有广泛的应用。自1963年Lorenz[1]在分析气候数据时发现了第一个混沌吸引子以来，从此拉开了混沌研究的帷幕。混沌控制也是近年来非线性动力学中引人注目的研究热点之一。1990年，Ott等开创性地提出了一种比较系统和严密的参数微扰方法，即OGY方法[2]，但该方法有一定的局限性。近几年来，国内外学者又相继提出了很多不同的控制方法[3-14]，这些方法各有优缺点，具体可以看文献。本文先对一个离散系统的动力学行为做了分析，然后提出一种控制方法对其有效的控制，数值仿真结果表明所提方法的正确性和有效性。

1 系统的动力学行为

非线性动力学系统往往含有一个或多个控制参数，如果当参数达到某个临界值时，系统运动轨道的拓扑结构将发生变化，这种现象称为分岔。分岔是一类常见的非线性现象，并且与其他非线性现象如混沌、分形等密切相关。Lyapunov指数是定量描述轨线收缩或扩张的量，可以表征系统的运动特征。

由分岔图可知系统是由倍周期分岔通向混沌的，混沌区域有几处长度不等的周期窗口。周期窗口对系统的动力学行为演变过程中起着十分重要的作用，会引发系统运行轨道状态突变或混沌危机等非线性物理现象。该系统具有和Logistic 映射相似的性质，都具有很强的自相似性。由Lyapunov指数图可知当系统的Lyapunov指数小于零时，对应系统处于周期运动。当Lyapunov指数大于零时，必将导致分岔图中的混沌区域。当系统Lyapunov指数从负值趋于零再到负值，系统在此点发生倍周期分叉；当系统Lyapunov指数从正值过零再到负值，系统在此点发生切分叉；当系统Lyapunov指数从负值过零再到正值，此点为系统从周期运动向混沌运动的过渡点[15]。图3给出了当系统参数= 0.6，= 1.2，= 1.4，= 4时的时间序列图，分别处于周期一不动点(a)，周期二不动点(b)，周期四不动点(c)和混沌态(d)。

图1 系统的分岔图

图2 系统的Lyapunov指数图

图3 系统的时间序列图

2 混沌控制

由于混沌控制在工程技术上的重大研究价值和十分诱人的应用前景，混沌控制引起了国际上非线性动力系统和工程控制专家的极大关注，成为非线性科学的研究热点之一。一般而言，混沌控制有以下几方面的含义，其一是引导问题，基于混沌吸引子内嵌有无穷多不稳定周期轨道，根据人们的意愿选择其中的一些（不动点或周期轨道）作为控制目标，选取适当的方法，在相空间中将混沌轨道引入事先指定的不动点或周期轨道的确定的小邻域内，这种控制不改变系统原有的周期轨道；其二是抑制问题，即不要求必须稳定控制原系统中的周期轨道，而是通过可能的策略，方法和途径，达到有效控制，得到所需的周期轨道，这条轨道不一定是系统原有的轨道，这种控制将改变系统动力学行为。

图4 受控系统的时间序列图

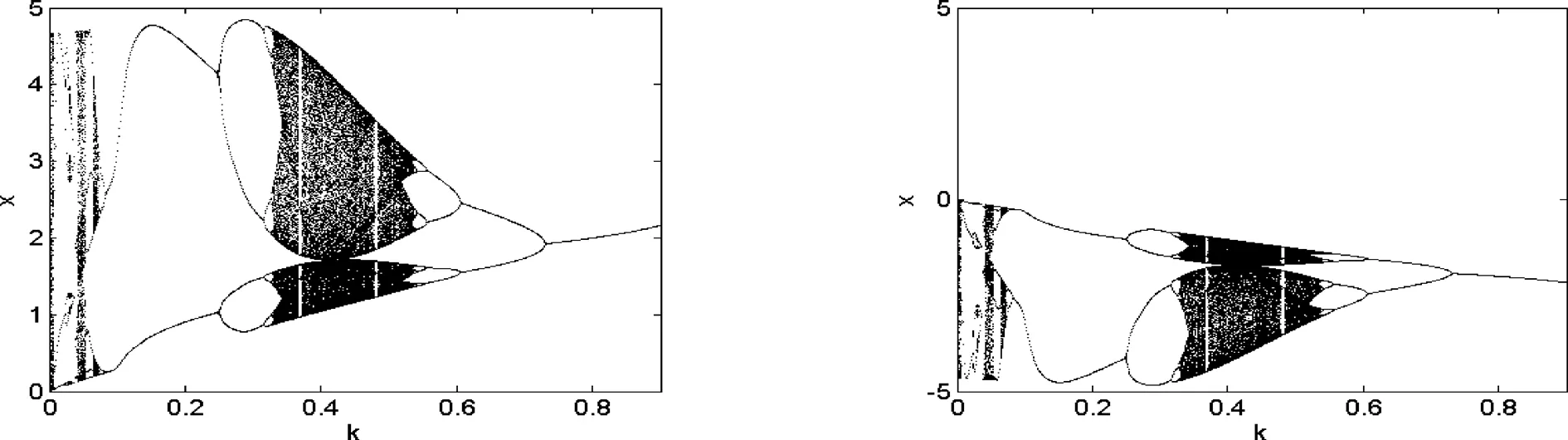
图5 受控系统的分岔图

3 结论

本文用数值计算的方法研究了一个离散系统的动力学行为和混沌控制。利用系统的分岔图和对应的Lyapunov指数图分析了系统由周期运动到混沌运动的转迁过程。然后提出了一种新的混沌控制方法，数值仿真结果说明了该方法的正确性和有效性。该方法可行，有效，代价小，而且控制速度快，编程方便，取得了令人满意的结果，可以推广到高维系统，因而在工程应用领域中具有广泛的应用前景。

[1] Lorenz E N.Deterministic nonpefiodic flow[J].At mos Sci,1963,20(2):130-141.

[2] Ott E,Grehogi C,Yorke J A. Controlling Chaos[J].Phys Rev Len,1990,64(11):1196-1199.

[3] 高继华,刘颖,彭建华.线性反馈法控制超混沌系统的高周期态[J].深圳大学学报,2003,20(3): 14-18.

[4] 李瑞红,徐伟,李爽．一类新混沌系统的线性状态反馈控制[J].物理学报,2006,55(2):598-604.

[6] 邹艳丽,罗晓曙,方锦清,等.用比例微分控制器实现混沌控制[J].广西师范大学学报,2002, 20(3):9-13.

[7] 李春来.永磁同步电动机中基于冲洗滤波技术的混沌控制研究[J].物理学报,2009,58(12): 8134-8138．

[8] 唐国宁,罗晓曙.混沌系统的预测反馈控制[J].物理学报,2004,53(1):15-20.

[9] 高智中.类Henon系统的混沌及其混沌控制[J].北京联合大学学报,2010,24(4):83-85.

[10] 高智中.一个新的混沌系统及其混沌控制研究[J].南京邮电大学学报,2011,31(1):106-110.

[11] 高智中.一类改进的Sprott-J系统的混沌及其不稳定平衡点的控制[J].盐城工学院学报,2011, 24(1):17-19,24.

[12] 高智中,叶苗,张程.一类新的混沌系统及其混沌控制[J].常熟理工学院学报,2011,25(4): 35-38,44.

[13] 高智中.一个新二维离散系统的分析及其混沌控制[J].荆楚理工学院学报,2011,26(7):48-51．

[14] 李 银,孙宇锋.非自治统一混沌系统的级联控制[J].井冈山大学学报:自然科学版,2011,32(2):33-36.

[15] 刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2005.

Chaos and chaos control of one-dimensinal discrete system

GAO Zhi-zhong

( College of Science, Anhui Science and Technology University, Fengyang, Anhui 233100, China)

Dynamic behavior of a class of one-dimensional discrete system is studied. We mainly analyze the transition from periodic motion to chaotic motion. We also design the chaos control scheme based on its movement characteristic. Numerical simulation results show the chaos control scheme can effectively control the chaotic state of the system.

bifurcation diagram; Lyapunov exponents diagram; chaos; chaotic control

N941.7

A

10.3969/j.issn.1674-8085.2012.02.008

1674-8085(2012)02-0031-04

2011-11-15；

2012-02-26

安徽省高校省级优秀青年人才基金项目(2012SQRL146)

高智中(1979-)，男，山西神池人，讲师，硕士，主要从事非线性动力系统分岔和混沌理论及其应用研究(E-mail: gaozhizhong2005@126.com)