气体分子扩散的蒙特卡罗模拟

晋宏营

气体分子扩散的蒙特卡罗模拟

晋宏营

（榆林学院能源工程学院，陕西，榆林 719000）

使用蒙特卡罗方法，对气体分子在背景气体中扩散的过程进行了计算机模拟，背景气体均匀分布于三维无界空间中。模拟结果显示，气体分子的扩散是各向同性的，扩散经历的时间越长，分子分布的范围越大，分子扩散的方均位移与时间成正比关系。使用本文的模拟方法还可估算气体扩散系数的数量级，对1标准大气压下、15°C时氧气的自扩散系数，以及氧气在氮气中的互扩散系数进行了估算，得到的扩散系数数量级与实验测量结果符合得很好。

蒙特卡罗方法；计算机模拟；扩散系数；方均位移

0 引言

当物质中粒子数密度不均匀时，由于分子无规则热运动，粒子将从数密度高的地方迁移到数密度低的地方，这类现象叫做扩散[1]。扩散现象在自然界中广泛存在，气体、液体和固体中都可以进行。对扩散现象的研究不仅在物理学中，而且在化学和生物学等学科中都具有重要意义，例如，生物体肺泡中的氧转移到毛细血管中，毛细血管中的CO2进入肺泡，就是通过扩散来进行的[1]。本文主要研究气体的扩散，使用蒙特卡罗方法模拟了气体分子的扩散过程，研究了扩散中分子的方均位移与时间的关系，并用模拟结果估算了气体扩散系数的数量级。

蒙特卡罗方法又称为随机取样法，是利用随机数的统计规律来进行计算和模拟的方法[2]。近年来，随着计算机的高速发展和普及，蒙特卡罗方法在很多领域得到广泛应用[3-5]。在物理学中使用计算机进行数值计算和模拟，不仅能够弥补简单的解析理论模型难以完全描述复杂物理现象的不足，而且可以克服物理实验中遇到的许多困难，具有传统理论物理和实验物理所不具备的优势[2]。例如我们可以使用蒙特卡罗模拟等计算物理方法，在计算机上直接模拟实验上不能实现或技术条件要求很高、实验代价昂贵的物理系统等，这方面的研究具有广阔的应用和发展前景。

1 蒙特卡罗方法模拟气体分子的扩散

取1000个分子为研究对象，使用Matlab语言，对它们在三维无界空间中的扩散进行了计算机模拟。设空间中均匀分布着某种背景气体，以空间中任一点为坐标原点建立球坐标系，假设初始时刻这1000个分子都聚集在坐标原点处，随着时间的推移分子向周围空间不断扩散。定义一个1000行×3列的矩阵，用来存放这1000个分子的位置；矩阵中的每一行表示一个分子，矩阵的第一列代表分子位置的坐标，第二列代表分子位置的坐标，第三列代表分子位置的坐标。再定义一个50000行×2列的矩阵，用来存放模拟中每一步对应的时间和此时的方均位移；该矩阵中每行的行序号代表模拟的步数，矩阵中各行的第一列用来存放时间，第二列存放方均位移<2>。

气体分子的扩散快慢取决于分子间相互碰撞的频繁程度[6]。每个分子在任意两次连续碰撞之间所通过的自由路程的长短和所需时间的多少，具有偶然性，对于研究气体的性质和规律，重要的是它们的平均值，即分子在连续两次碰撞之间所通过的平均自由程，以及连续两次碰撞之间所需的平均时间。设分子的平均碰撞频率为，则连续两次碰撞之间所需的平均时间Δ=1/[6]。我们让各分子每经过Δ时间移动一个步长，步长大小取为平均自由程，移动的方向是随机的。我们在模拟中用“A=rand(1,2)”命令生成了两个在0—1之间均匀分布的随机数A(1)和A(2)，来决定分子在空间中运动的方向，A(1)决定分子球坐标中的角，A(2)决定球坐标中角的余弦值cos。分子在空间中的运动方向是各向同性的，即按立体角均匀分布，这就要求分子的球坐标中，角在0—2π之间均匀分布，这通过命令“=A(1)*2π”实现；而角的余弦值cos在-1—+1之间均匀分布，这通过命令“cos=2*A(2)-1”实现。

设分子上一步的直角坐标为(0,0,0)，下一步的直角坐标为(,,)，则由球坐标与直角坐标的关系，可得：

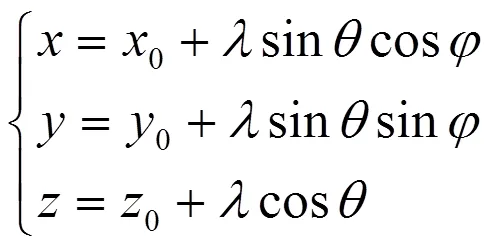
式中为分子运动的平均自由程，设经过时间任一分子扩散到与原点距离为r的位置，则

在同一时刻，对1000个分子分别到原点的距离的平方求和，再除以1000即得此时刻的方均位移，即

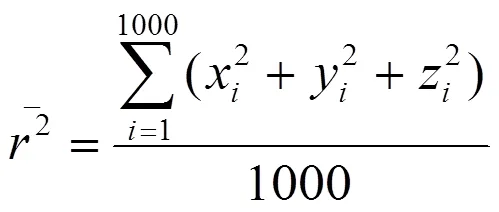
不同气体或同种气体在不同温度和压强下的平均自由程和平均碰撞频率是不同的，在模拟过程中，取步长为1，两步之间的时间间隔也取为1，这相当于以分子的平均自由程为长度单位，以分子在连续两次碰撞之间运动的平均时间为时间单位，这样无量纲化处理后，更便于计算机模拟。

2 模拟结果与分析

2.1 模拟中使用的随机数质量的检验

上面设计了一个使用蒙特卡罗方法对1000个分子在三维无界空间中扩散进行模拟的模型。模拟结果的好坏与模型中使用的随机数的质量直接相关[2]，我们对随机数的随机性好坏进行了检验：

模型中的随机数决定了分子运动的方向，让所有分子都从原点位置移动一个步长，如果使用的随机数随机性很好，则由于空间各向同性，这1000个分子在各个方向上应该均匀分布，没有哪个方向占优势，故它们应该均匀分布在一个以原点为球心，步长为半径的球面上。检验结果见图1，从图中可看出，1000个分子确实是均匀分布在以步长为半径的球面上的，这说明所使用的随机数随机性较好。

2.2 分子扩散过程的观察

根据理论分析以及实验结果[7-8]，对于大量分子从同一位置处开始向周围空间扩散的过程，中心处的分子数密度应大于四周的分子数密度，离中心越远，分子数密度越小；分子扩散的时间越长，则分子分布的范围越大。我们分别作出了经过5000步和50000步模拟之后分子分布的散点图，见图2和图3。

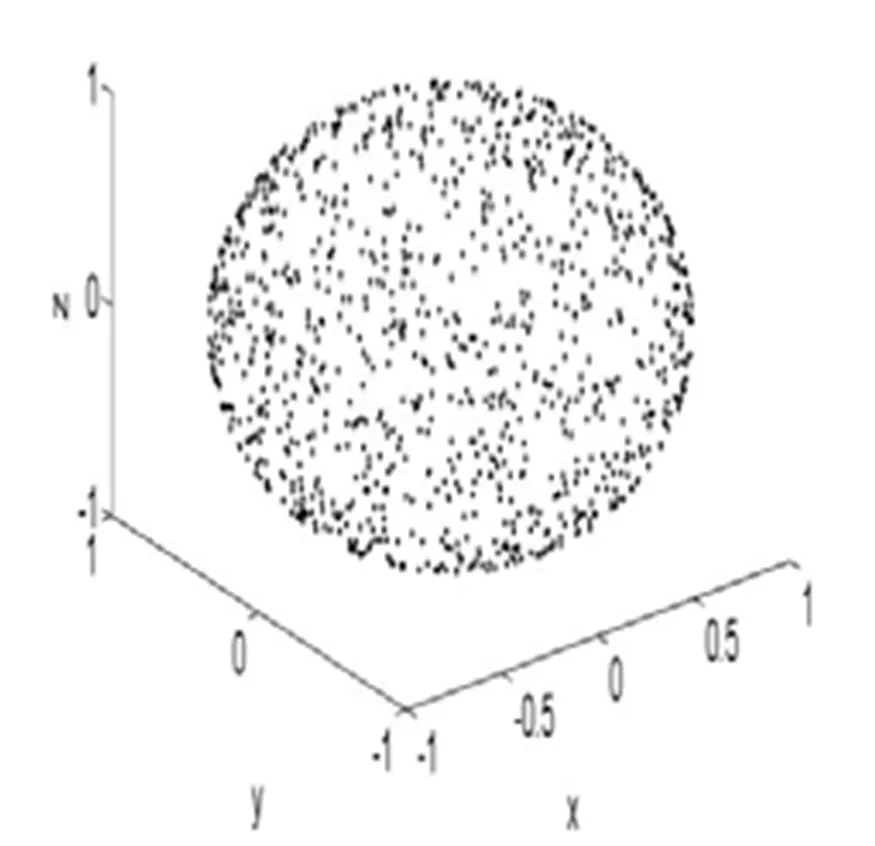
图1 各分子均走一步后分子分布的散点图

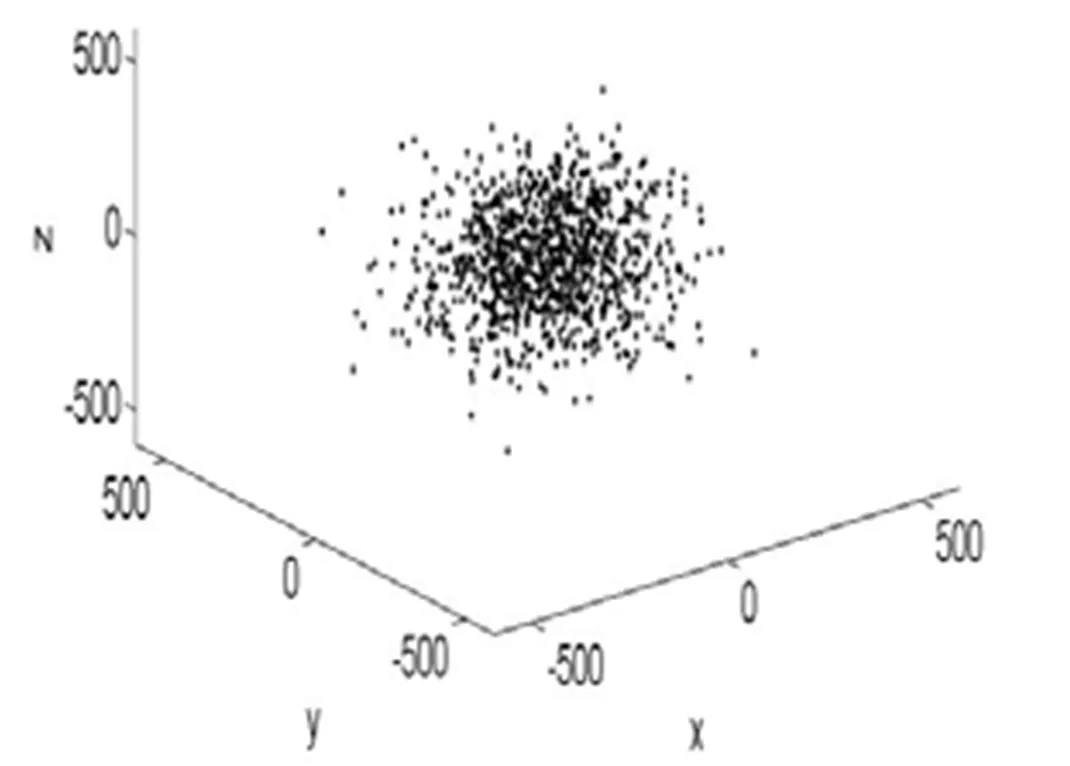
图2 5000步模拟后分子分布的散点图

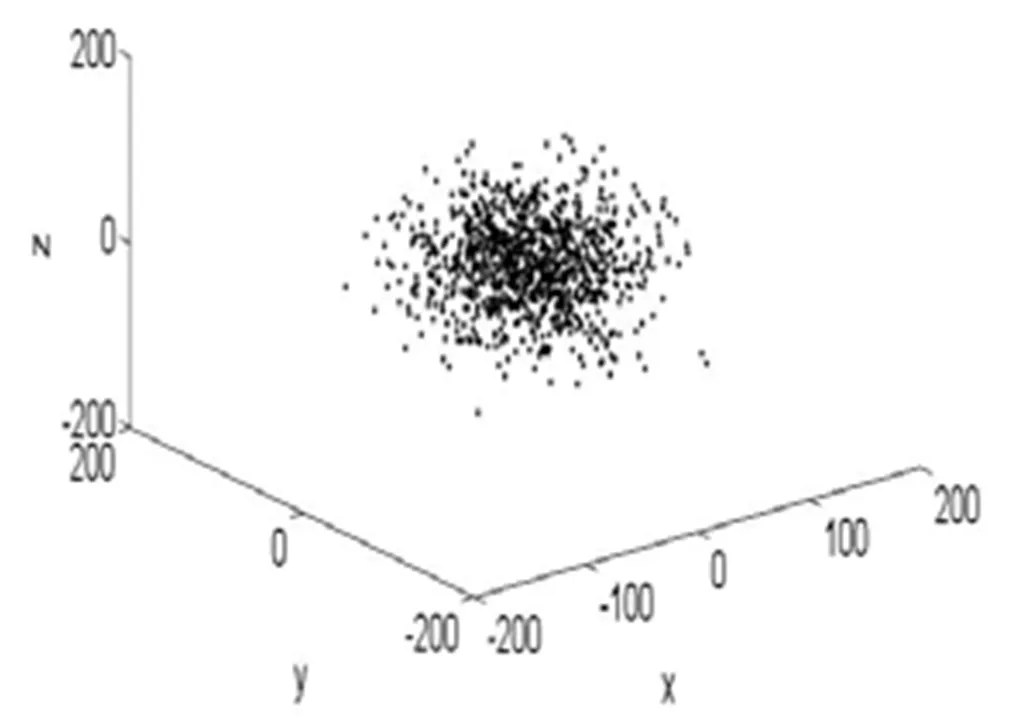
图3 50000步模拟后分子分布的散点图

从图2和图3中可以看出，两幅图中分子的分布均以坐标原点为中心，呈各向同性的球对称分布，没有哪个方向的分子数占优势。越靠近坐标原点，分子数密度越大，越往外则分子数密度越小。对比图2和图3可见，经50000步扩散之后，分子的分布范围明显大于经5000步扩散之后的，这说明扩散经历的时间越长，分子分布的范围越大。由此可见，模拟结果与理论分析及实验结果符合得很好。

2.3 方均位移与时间关系的模拟结果

根据布朗运动和扩散的理论及实验结果，扩散过程中分子的方均位移与扩散时间成正比[7-8]。我们利用程序运行模拟了方均位移与时间的关系曲线，并用最小二乘法拟合了该曲线的斜率，模拟结果见图4，最小二乘法拟合的曲线斜率为=1.01。

从图4可以看到，模拟得到的方均位移与时间之间是呈正比关系的，这与理论和实验结果符合的很好。

2.4 估算气体扩散系数的数量级

利用模拟得到的方均位移与时间的关系曲线可以估算气体扩散系数的数量级，下面我们对氧气在温度为15℃（288 K），压强为1标准大气压（1.013×105Pa）时的自扩散系数，以及在相同的温度和压强条件下，氧气在氮气中扩散的互扩散系数进行数量级估计。

2.4.1 氧气自扩散系数的估计

在温度= 288 K，压强=1.013×105Pa时，氧气分子的有效直径为=3.6×10-10m[6]，据此可求得该条件下，氧气分子的平均自由程为：

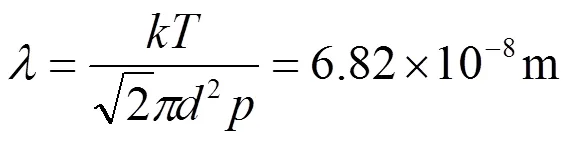
式中的为玻耳兹曼常量。还可求得氧气分子的平均碰撞频率为：

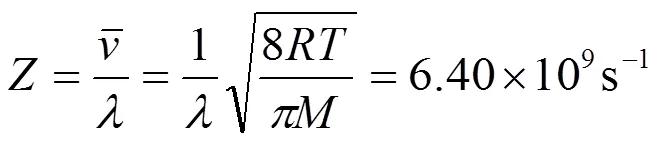
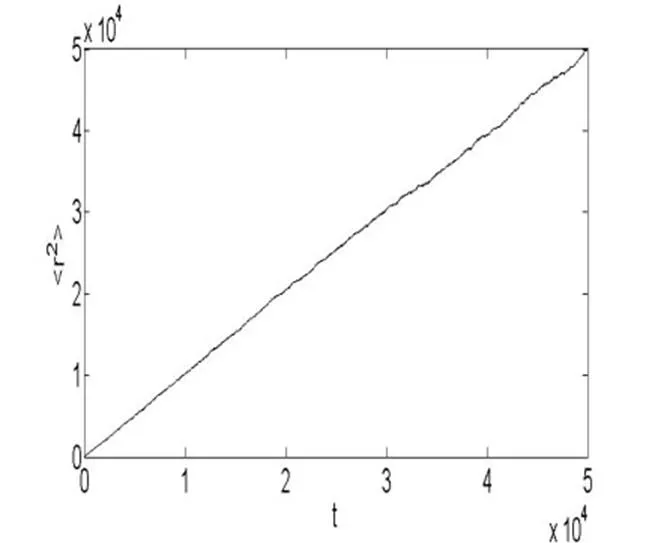
图4 方均位移与时间的关系曲线

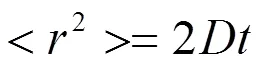
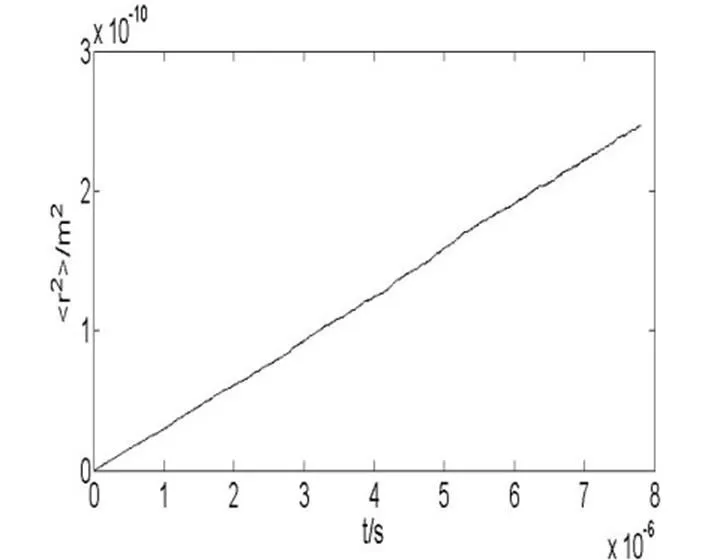
图5 氧气分子自扩散时方均位移与时间的关系

文献[1]指出，对于常温常压下的大多数气体，扩散系数的值约在10-5~10-4m2/s之间。该文献还给出了1标准大气压和常温下一些气体扩散系数的实验结果，其中氧气的自扩散系数为1.89×10-5m2/s。我们模拟得到的氧气自扩散系数的数量级与此符合的很好，这说明，使用我们的模拟方法，可以很好地估计气体自扩散系数的数量级。

2.4.2 氧气在氮气中互扩散系数的估计

在温度=288 K，压强=1.013×105Pa时，氧气分子的有效直径1=3.6×10-10m，氮气分子的有效直径2=3.7×10-10m[6]。据此可求出氧气分子在氮气中扩散时的平均自由程为[1]：

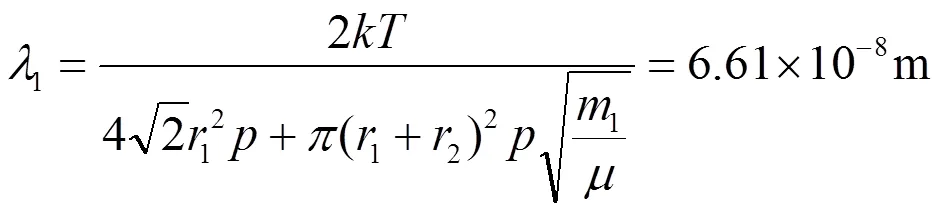
此时的平均碰撞频率为：

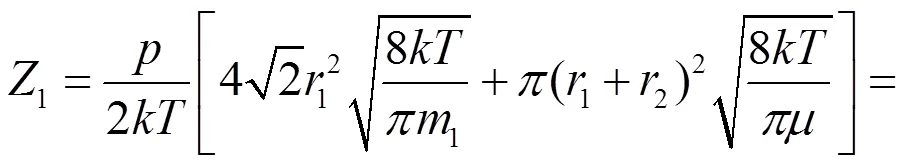
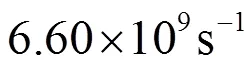
因此Δ=1/1=1.52×10-10s。

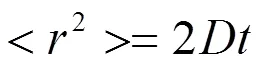
图6 氧气在氮气中互扩散时方均位移与时间的关系

文献[1]给出的在1标准大气压和常温下，氧气在氮气中的互扩散系数的实验值为1.74×10-5m2/s。我们的模拟结果与此实验值从数量级来说符合的很好。由此可见，无论是气体的自扩散还是互扩散系数，我们的模拟方法都可以给出很好的数量级估计。

[1] 秦允豪.热学[M] .北京:高等教育出版社,1999.

[2] 彭芳麟.计算物理基础[M] .北京:高等教育出版社,2010.

[3] Rasmussen C J,Vishnyakov A,Neimark A V. Monte Carlo simulation of polymer adsorption [J].Adsorption, 2011, 17: 265-271.

[4] Preis T, Virnau P, Paul W, et al.GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model[J]. Journal of Computational Physics, 2009, 228: 4468-4477.

[5] Fang Q Q, Boas D A. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units [J].Optics Express, 2009, 17(22): 20178-20190.

[6] 李椿.热学[M].2版.北京:高等教育出版社,2008.

[7] 汪志诚.热力学统计物理[M].4版.北京:高等教育出版社,2008.

[8] Kampen V. Stochastic Processes in Physics and Chemistry [M]. Amsterdam: North Holland Publishing Company, 2004.

MONTE CARLO SIMULATION OF DIFFUSION OF GAS MOLECULES

JIN Hong-ying

(College of Energy Engineering, Yulin University, Yulin, Shanxi 719000, China)

Based on Monte Carlo method, a computer simulation is performed to study diffusion process of gas molecules in background gas, which is uniformly distributed in three-dimensional unbounded space. The simulation results show that diffusion of molecules is isotropic which the longer diffusion time, the larger distribution range of molecules and the mean square displacement are proportional to time. The simulation method can be used to calculate the order of magnitude of diffusion coefficients of gases. The self-diffusion coefficient of oxygen and the mutual diffusion coefficient of oxygen and nitrogen are estimated at 1 atmosphere and 15 °C. The calculated order of magnitude of diffusion coefficients is in good agreement with experimental results.

monte carlo method; computer simulation; diffusion coefficient; mean square displacement

O552.2

A

10.3969/j.issn.1674-8085.2012.02.007

1674-8085(2012)02-0027-04

2011-12-24；

2012-02-18

陕西省教育厅科学研究项目(2010JK933)；榆林学院高学历人才科研启动基金项目(11GK04)；能源工程学院教改项目

晋宏营(1972-)，男，山西浑源人，讲师，博士，主要从事理论生物物理研究(E-mail:jhy312@sohu.com).