支持向量机在齿轮故障诊断中的应用
2012-10-21张全林余新亮
李 力 张全林 李 骥 余新亮
(三峡大学 机械与材料学院,湖北 宜昌 443002)
齿轮作为机械设备的关键传统件,其运行状态关乎整个设备的可靠性与稳定性,齿轮故障检测和诊断方法的研究也备受重视.目前一些常用的故障诊断方法如人工神经网络等,都需要大量的训练样本,但在实际工程中大量的故障样本数据难以获得,使得这些方法的应用受到一定限制[1].
建立在统计学习理论基础上的支持向量机(Support Vector Machine)是一种专门研究小样本情况下的新型机器学习方法,它具有完备的理论基础,在解决小样本、高维模式识别问题中表现出许多特有的优势,能够在有限的样本条件下,最大限度地挖掘数据中的隐含特征.因此,针对齿轮小样本故障数据,本文采用SVM进行齿轮故障诊断,以提高小样本情况下的诊断准确率.
1 SVM分类原理
对于给定的内积空间H,存在超平面{(w·x)+b=0|x∈H,w∈H,b∈R}将样本集T 分离.其中,w是一个垂直于超平面的向量,设w为单位长度,则(w·x)是向量x沿w方向的长度.SVM是从线性可分情况下的最优分类面发展而来的,基本思想可用图1所示的二维平面来说明.图1中,小方框和圆圈分别代表两类样本,中间的实线为分类线,其附近的两条虚线分别为过各类中离分类线最近且平行于分类线的直线,它们之间的距离为分类间隔.所谓最优分类线就是要求分类线不但能将两类正确分开,即训练错误率为零,而且使分类间隔最大.对分类线(w·x)+b=0进行标准化处理,使得分类间隔等于2/‖w‖,使间隔最大等价于使‖w‖/2最小.训练样本正确可分,且使‖w‖/2最小的分类面就是最优分类面,位于两虚线上的训练样本点就称作支持向量[2].则构建最优超平面的问题可以转化为最优化(二次规划)问题:min(‖w‖2/2).实际故障诊断应用中,需要解决的常常是非线性的多类分类问题,解决这个问题的3个步骤为[2-3]:
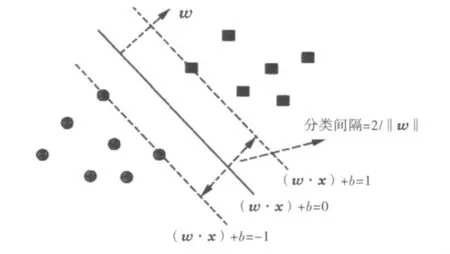
图1 两类线性分划的最优超平面
step 1:在线性可分的基础上增加一个松弛项ξi≥0和惩罚因子C,将约束放宽,目标函数为:

式中,C为可调参数,表示对某种故障识别错误的惩罚程度,C越大惩罚越重.
step 2:根据泛函的有关理论,寻找一种核函数K(x,y)=φ(x)φ(y),通过非线性映射φ:Rn→H,将输入变量映射到高维Hilbert空间H中.此时非线性SVM转化为高维空间中线性最优化问题:
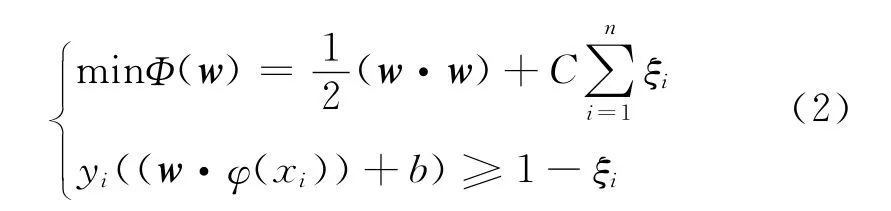
常用的核函数有线性核函数、多项式核函数、径向基核函数和sigmoid核函数,根据文献[4-5]指出,在大多数情况下径向基核函数分类法将获得更高的分类精度,选择径向基核函数:K(x,y)=exp(-γ·‖x-y‖2),γ>0,此核函数仅有一个参数γ,在训练优化过程中,大大降低运算量.
step 3:采用分解法,即通过某种方式构造一系列标准的两类SVM分类器,并将它们组合在一起来实现多类分类.针对齿轮故障诊断分类器,选择OVO(one vs.one)方法[6]进行快速训练建模,对于k类分类问题,OVO方法构造k(k-1)/2个SVM分类器模型为
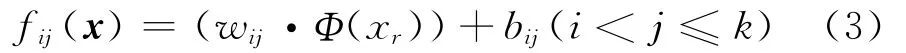
2 齿轮故障诊断应用
2.1 齿轮振动信号采集
获取齿轮振动状态信号.试验采用齿轮故障试模拟试验台,它由控制台、直流电动机、加载电机、直流调速加载系统、齿轮减速箱组成.故障信号源来自齿轮箱,其传动简图如图2所示,上面布置有各种模拟故障.其中,输入轴与输出轴上齿轮Z1、Z4均为正常齿轮(Z1=26,Z4=85,m=2mm);中间轴上,Z2为一个正常、一个有故障(Z2=64,m=2mm)的二联齿轮;Z3为一个正常、两个有故障(Z3=40,m=2mm)的三联齿轮.不同故障状态通过调节齿轮箱前后换档手柄获得.
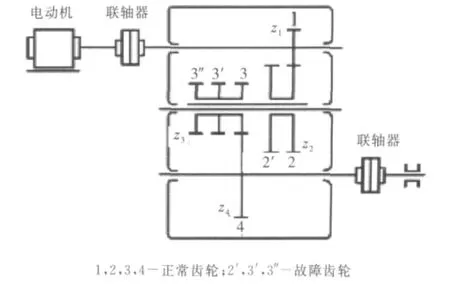
图2 齿轮箱传动简图
由于故障齿轮在啮合过程中常伴有高频振动信号的产生,振动信号频带在1Hz~10kHz之间,故采用加速度传感器测取齿轮信号,选取齿轮箱中间轴两侧轴承座附近刚性较好的部位安装传感器.数据采样频率为20kHz,数据序列长度N=8 192,输入轴转速1 000r/min.分别采集齿轮4种状态的信号(正常、磨损、剥落和断齿),每种状态采集40组数据,共160组数据.
2.2 SVM分类诊断
2.2.1 特征提取
提取信号特征作为SVM的输入特征向量.机械信号常见的特征有时域特征、频域特征、时频域特征及能量特征等.基于时域统计特征的无量纲指标满足对机器的状态敏感和运行参数不敏感的要求,且从不同方面反映机器状态变化的物理本质[7],因此,本文选取识别能力较强的标准差、峭度指标、偏度指标、峰值指标、波形指标、脉冲指标、裕度指标和能量特征共8个参数,得到8维特征向量.限于篇幅,列出齿轮4种状态前5组信号的特征向量见表1.
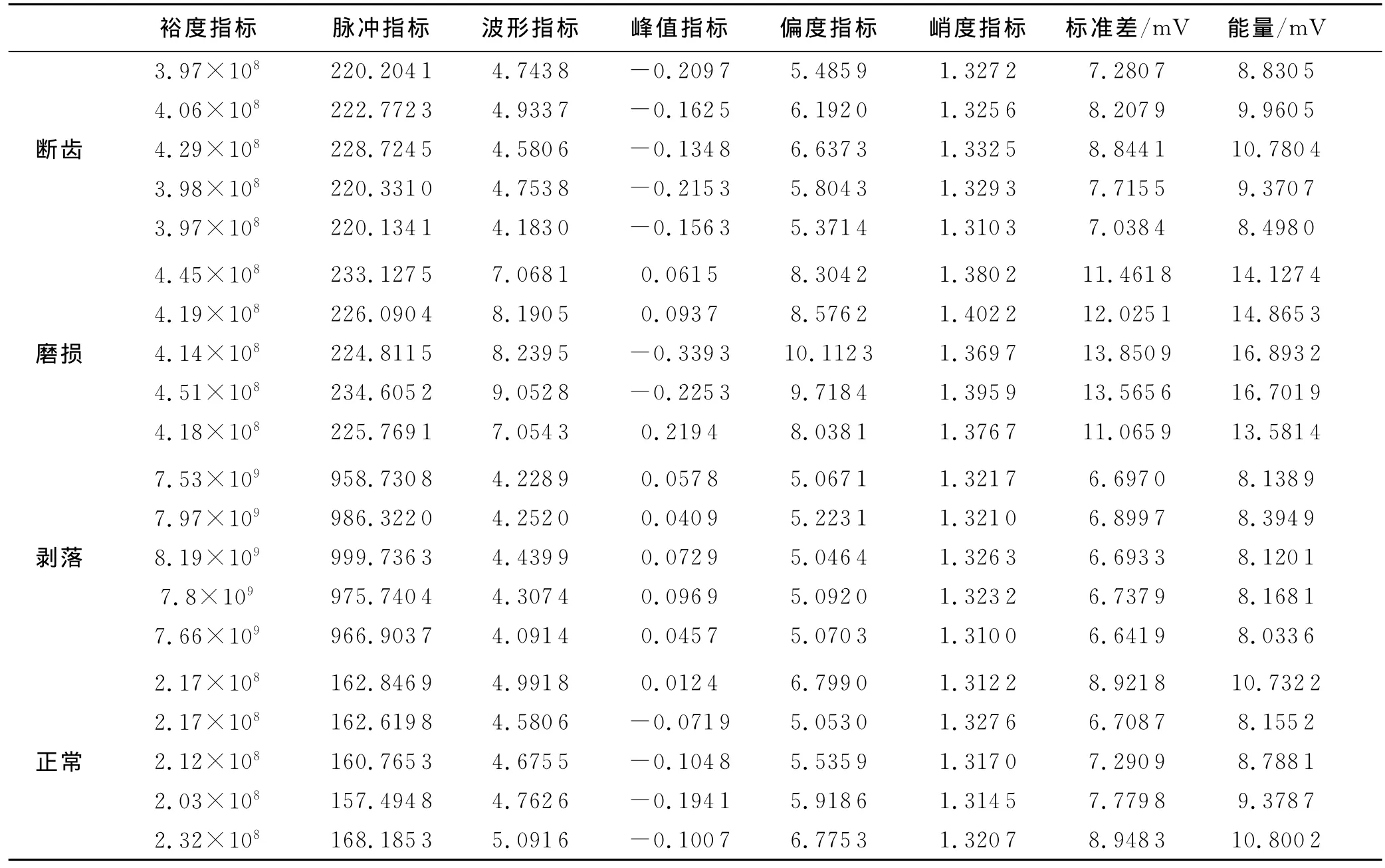
表1 齿轮4种状态下的特征向量
2.2.2 SVM参数选取与故障分类
SVM实现过程中要确定两个参数,即核函数参数γ和惩罚因子C.采用K-CV方法进行参数优化[8],最佳参数搜索优化过程如图3~4所示.先使用粗网格(如图3所示)在2-10~210上进行粗略搜索,找到最佳参数C,γ的范围分别为2-2~24,22~26,随后再在该领域上进行精确搜索(如图4所示)找到K-CV方法下的最佳参数.
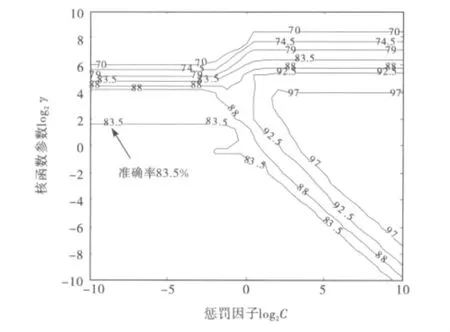
图3 粗略选择参数的准确率等高线图
搜索结果表明,C=22,γ=23时,SVM取得最优的故障识别精度,由此得到基于SVM的齿轮诊断分类结果见表2.由表2可知,SVM不仅将齿轮正常状态与故障状态完全识别,而且也能够完全正确地识别出齿轮两类不同属性(局部故障与均布故障)的故障;对同类故障(均布故障)下的两种不同故障模式(磨损、剥落)识别率也达到100%,其多故障的识别率为100%,达到了故障诊断要求.

图4 精确选择参数的准确率等高线图
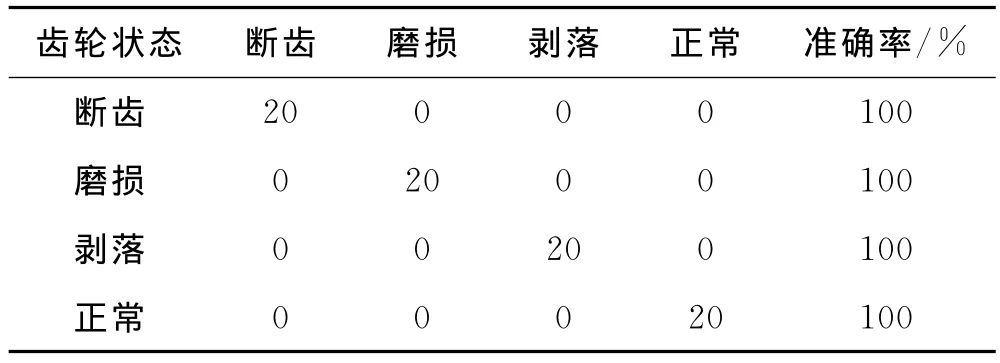
表2 SVM分类结果混淆矩阵
3 结 论
1)SVM参数直接影响其分类精度,利用K-CV网格搜索法优化分类器参数,可以有效地提高诊断准确率.
2)采用基于参数优化的SVM正确识别出齿轮的4种不同运行状态,其故障诊断准确率为100%,诊断效果显著.
3)SVM适合于解决小样本故障诊断问题,是一种先进的智能故障诊断方法,在状态监测与故障诊断方面具有良好的应用前景.
[1] 朱颖辉,李友荣,刘安中,等.SVM在齿轮小样本故障诊断中的应用[J].煤矿机械,2006,27(11):186-188.
[2] 邓乃扬,田英杰.数据挖掘中的新方法-支持向量机[M].北京:科学出版社,2004.
[3] 刘志刚,李德仁,秦前清,等.支持向量机在多类分类问题中的推广[J].计算机工程与应用,2004(7):10-13.
[4] Christopher J C.Burges.A Tutorial on Support Vector Machines for Pattern Recognition[J].Data Mining and Knowledge Discovery,1998(2):121-167.
[5] 于德介,陈淼峰,程军圣,等.一种基于经验模式分解与支持向量机的转子故障诊断方法[J].中国电机工程学报,2006,26(16):162-167.
[6] Chih-wei Hsu,Chih-Jen Lin.A Comparison of Methods for Multiclass Support Vector Machines[J].IEEE Trans On Neural Networkss,2002,13(2):415-425.
[7] 李 力.机械信号处理及应用[M].武汉:华中科技大学出版社,2007.
[8] Yoshua.No Unbiased Estimator of the Variance of KFold Cross-Validation[J].Journal of Machine Learning Research,2004,1089-1105.
