滑动窗口MF－DFA方法在大坝变形监测中的运用

王松林 邵晨飞 朱 蓓 张超波

（1.河海大学 水利水电学院，南京 210098；2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；3.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098）

分形现象［1］普遍存在于大自然中，如海岸线的形状、食品价格、水库蓄水量等.2002年Kantelhardt等人提出了多重分形消除趋势波动分析方法（Mltifractal detrended fluctuation analysis，MF－DFA），该方法已经被成功应用在与时间序列有关的诸多领域，它的优点在于可以系统地滤去各阶的趋势成分，可以检测含有噪声且叠加有多项式趋势信号的相关性，容易被人们理解和使用，适合于非平稳时间序列中的幂律相关分析，有效避免了将系统的短期相关或非平稳性虚假检测为长期相关.

由于影响大坝变形的因素往往是复杂的，仅用单一分形来分析大坝结构的工作形态显然欠妥，在此将包括单一分形在内的多重分形对大坝变形进行分析，可以提供更多的信息为大坝的安全运行服务.本文运用MF－DFA对大坝变形规律进行研究，可从复杂的大坝位变性态中发现其内在的、有序的、确定的规律，更全面地解释在各种荷载作用下大坝的复杂变形特征［2］.由于MF－DFA方法没有考虑因数据分割点的不连续性所产生的影响，本文引入滑动窗口技术加以改进，提升了传统MF－DFA方法的精度.

1 滑动窗口MF－DFA的基本原理

多重分形消除趋势波动分析方法［3－6］具体步骤如下：

步骤1：对给定的时间序列x（t）求对于均值的累积离差，产生一个新序列y（i）：

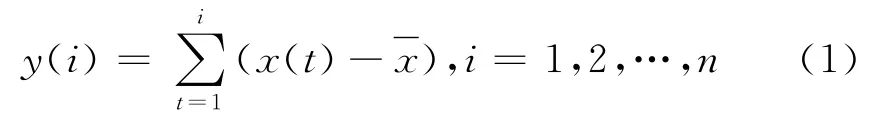
步骤2：将变换得到的新序列y（i）分割成长度为s的m 个互不重叠的等长子区间，其中m＝int（n／s），即对n／s进行取整处理.由于n未必能整除s，为了避免不丢失尾部信息，对新序列y（i）逆序进行同样分割，使得序列y（i）全部数据均进入计算，最终得到2m个等长子区间.

步骤3：通过最小二乘法拟合每个子区间v（v＝1，2，…，2m）上的局部趋势函数yv（i），其中yv（i）为第v个子区间对s个观察值进行k阶多项式拟合，得到拟合方程：

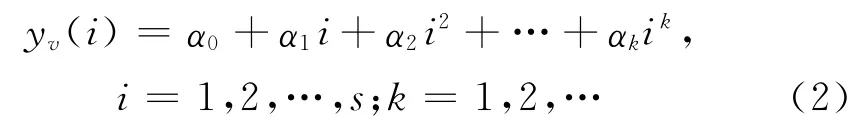
式中，αk（k＝1，2，…）为最小二乘拟合的系数.

步骤4：通过消除每一子区间v中的趋势得到相应残差序列，计算2m个子区间的残差序列平方和H（q）：

当v＝1，2，…，m 时，

步骤5：对于2m个子区间计算F2（v，s）的均值，得到整个序列的q阶波动函数Fq（s）：

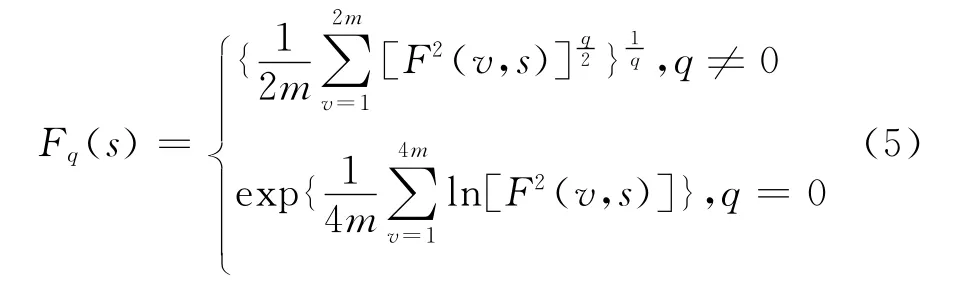
当q＝2时，多重分形MF－DFA就退化成单一分形；当q＜2时，Fq（s）的大小取决于小波动的均方误差F2（v，s）的大小；当q＞2时，Fq（s）的大小取决于大波动的均方误差F2（v，s）的大小.因此，不同的q取值就描述了不同程度的波动对Fq（s）的影响程度.

步骤6：对于大量的s和给定的阶数q，通过在双对数图中观察两者之间的关系，有Fq（s）＝AsH（q），两边取对数可得：lnFq（s）＝lnA＋H（q）ln（s），采用最小二乘法进行线性回归，得到斜率估计值即为标度指数H（q），反映出原始数据序列与时间序列的相关性.

为了使得Fq（s）有较高的稳定性，通常s取值为6≤s＜int（n／6）.当采用不同q值计算出来的H（q）值大小与阶数q无关时，则表明序列x（t）是单一分形过程；当计算出来的H（q）值大小随阶数q变化，则序列x（t）是一个多重分形过程.

滑动窗口MF－DFA法的主要思路是对传统MFDFA的区间分割方法采用滑动窗口技术进行改进，有效解决了因传统MF－DFA法在多项式拟合时分割数据连接处的不连续性产生的新伪波动误差，也充分避免在数据分割时丢失尾部数据信息，或对数据逆序处理时因打乱原始数据序列导致的H（q）误差.

滑动窗口MF－DFA法具体步骤改变仅表现在：步骤2中将传统MF－DFA法中互不重叠的区间分割法用滑动窗口的连续重叠区间分割来代替；步骤五中波动函数Fq（s）的相应改变，即

2 工程实例分析

以某混凝土重力坝某测点的变形监测数据为例（如图1所示），探讨滑动窗口 MF－DFA法在大坝变形中的应用，并与传统MF－DFA法进行比较分析.

具体操作方法如下：取s＝8，9，…，100，q＝－10，－9，k＝1，2，3，4.分别用传统 MF－DFA法和滑动窗口MF－DFA法计算大坝某测点的标度指数H（q）值.计算结果见表1，H（q）对q的散点图如图2所示.

图1 大坝变形轮廓曲线

从表1的实例分析结果和图2可得到如下结论：

1）对于给定的k阶拟合多项式，无论是传统MFDFA法还是滑动窗口MF－DFA法，大坝变形原始监测序列的H（q）值均不为常数，而且呈现的非线性关系极为相似，均表现为q的递减函数，因此可以认为大坝变形随时间序列均具有不同程度的多重分形特征，用单一分形无法进行完整描述.

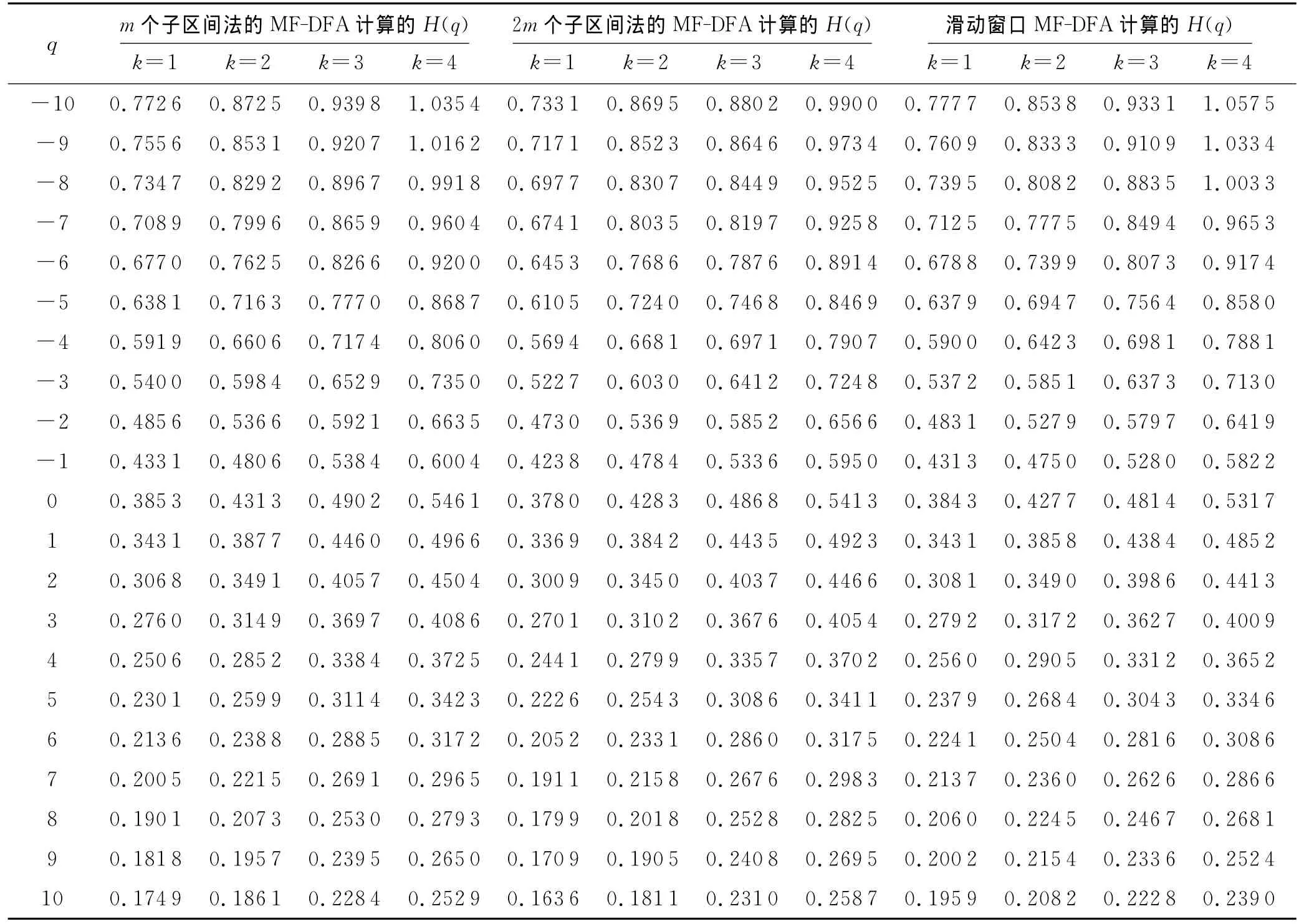
表1 3种MF－DFA计算方法下的大坝变形序列H（q）值表

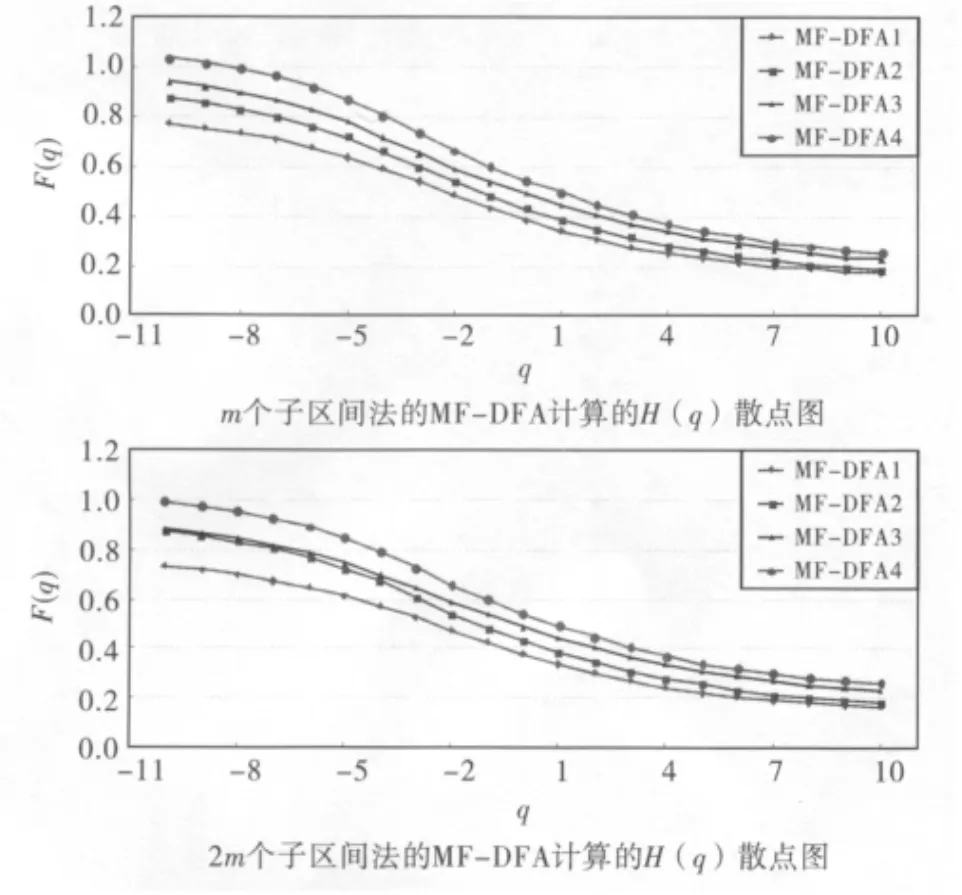
图2 3种MF－DFA计算方法下的H（q）散点图

2）对于任意q值和k阶多项式拟合，构造2m个子区间的多重分形特征比直接构造m个子区间的多重分形特征强，而采用滑动窗口 MF－DFA比传统MF－DFA法所得的H（q）值普遍都大，说明大坝变形序列表现出显著的相关性且具有多重分形特征.

如果采用m个子区间分割法进行多重分析，由于存在丢失尾部数据信息的缺陷，会对分析结果产生严重误差，从实例可得H（q）值较另两种方法均要偏小；如果采用2m个子区间分割法分析，虽然在一定程度上解决了数据未充分利用的缺陷，但进行逆序分割时打乱原始数据的顺序会减弱多重分形波动分析的结果，不可避免地将影响分析的客观性；而滑动窗口MF－DFA法能充分避免上述两种情况存在的分析误差，较前两种分析方法具有较高的精度和可信性.

3）当q值一定时，H（q）值随着k值的增加而增加.显而易见，对每一个区间上的s个观察值进行k阶多项式的目的在于从累加序列y（i）中消除k阶趋势波动，同时在原始序列中消除k－1阶趋势波动，因拟合精度提高从而使得H（q）值的增加.因此，时间序列的波动程度越大，使用不同阶的 MF－DFA法对H（q）进行估计的差异也就越大.

4）在k＝2的情况下，当q＜0时滑动窗口 MFDFA法分析的H（q）值偏小，当q＞0时滑动窗口MF－DFA法分析的 H（q）值偏大，则说明 H（q）值更快趋于更稳定的数值，相比k＝1和k＝3两种情况，2阶多项式拟合能较稳定地反映大坝结构形态.

下面采用2阶多项式拟合的滑动窗口MF－DFA法对大坝变形数据序列进行分析，作出lnFq（s）～ln（s）的函数关系图（如图3所示），应用最小二乘线性回归拟合该散点数据，其斜率即为所得的标度指数H（q）.在q＝2情况下，H（q）＝0.345，此时相关系数R＝0.975.这说明大坝该测点整体数据系列存在较强的长程相关性，即大坝在一段时间内由于荷载变化（如水位的上升或下降，温度的升高或降低等）向上游移动后，在下一段时间内因同种荷载效应则倾向于向下游移动，它比随机序列有更强的突变性和易变性，同时在轮廓曲线上表现为多“噪声”.

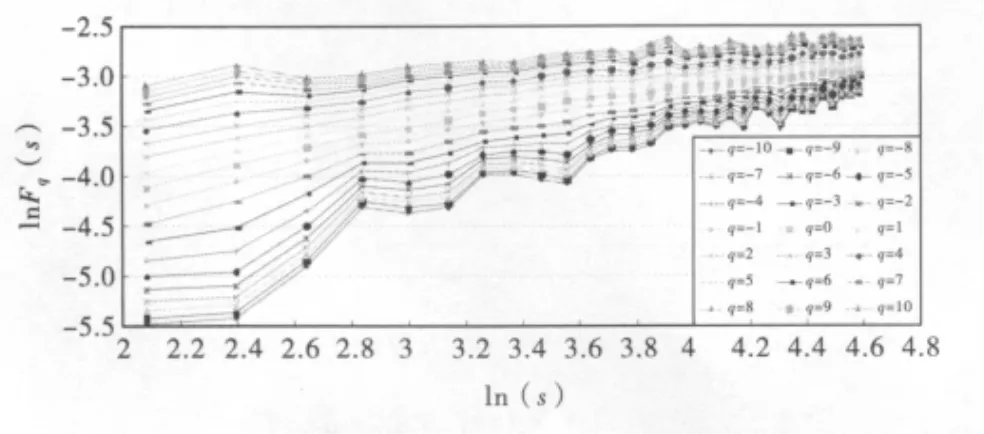
图3 lnFq（s）－ln（s）的关系图

3 结 语

1）采用滑动窗口MF－DFA法对大坝结构性态进行研究，发现大坝变形呈现明显的多重分形特征，解决了传统MF－DFA法存在的缺陷，提高了分析结果的精度.

2）为了准确地估计H（q），观察值s取值要适中，太小没有实际意义，太大则分割区间太少，统计结果上不可靠；权重因子q的选择对结果影响重大，目前未形成统一标准，上述取值人为因素较大，有待进一步研究.

3）通过分析比较3种方法，选用2阶多项式拟合的滑动窗口MF－DFA法对变形数据序列是否具有相关性进行分析，从而断定大坝将来的变化趋势，对后续建模预测的数据选择具有一定的指导作用，也是本文以后的研究方向之一.

［1］ 李水根.分形［M］.北京：高等教育出版社，2006：1－200.

［2］ 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006：180－200.

［3］ 赵 卿，黄声享.非倾向性振荡分析用于变形监测数据分析的探讨［J］.测绘科学，2009，34（3）：52－53.

［4］ 燕爱玲.河川径流时间序列的分形特征研究［D］.西安：西安理工大学，2007：75－96.

［5］ 许 林，宋光辉，郭文伟.基于改进MF－DFA的基金市场风格资产价格波动研究［J］.广东金融学院学报，2011，26（1）：65－76.

［6］ 袁平平，于建玲，商朋见.股市时间序列的多重分形消除趋势分析［J］.北京交通大学学报，2007，31（6）：69－72.