格构梁刚度及地基变形模量对格构梁弯矩的影响研究

2012-10-21王志俭赵家成

三峡大学学报(自然科学版) 2012年2期

王志俭万诚赵家成

（三峡大学三峡库区地质灾害教育部重点实验室，湖北宜昌 443002）

在众多支护结构中，锚杆格构结构是一种新型的抗滑支档结构，它是把锚索工程和格构梁护坡两者相结合而形成的，适合于节理发育、坡度较陡、容易受到自然应力的影响导致大面积的碎落及局部小型落石、崩塌的岩质边坡.格构锚固结构不仅可以进行深层加固又可兼顾浅层护坡，近年来广泛应用于地质灾害防治中.格构梁的组成包括横梁和纵梁，在对格构梁的内力进行计算时，通常将交叉的格构梁视为单根格构梁进行计算.其中可以运用到弹性地基梁的研究成果［1］.在弹性地基梁的内力计算中，Winkler地基模型由于计算简便，在工程实际中大多采用这一地基模型［2－3］.此外还有双参数地基模型，它采用两个独立的参数来表征地基土的特性，将格构梁作为双参数地基上的梁，通过求解地基反力，进而求解出梁的内力和变形.但是Winkler地基模型和双参数地基模型不能完整地反映实际的地基变形情况，因为他们都忽略了地基变形的连续性［4］，必然会对密实土层和岩石地基的研究造成较大误差.为了避免这种情况，可以改成半无限弹性地基模型.

半无限弹性地基模型起源于经典连续介质力学的成果，当把这些结果用于土与结构相互作用课题时，在数学计算上有较大的困难.幂级数法是常用的方法，将地基反力p（x）近似地表达为有限项的幂级数：

式中，a0、a1、a2、…、an就是所求的n＋1个基本未知量，利用两个静力平衡方程和n－1个变形连续方程（在n－1个点处梁的挠度和地基沉陷相等），可解出基本未知量.因此，问题归结为解n＋1个代数方程.

目前除用幂级数法求得挠度和沉降的相对值外，基于半无限弹性地基假定的近似解决方法有：链杆法、郭氏法、蔡氏法等.这些计算方法虽然平衡条件被准确满足，但接触条件则是近似满足的.

在实践中，采用半无限弹性地基模型的地基梁问题多采用数值方法计算.本文运用FLAC3d软件，通过数值试验的方法，研究地基变形模量E0，格构梁弹性模量E及格构梁惯性矩I这3个参数对格构梁内力的影响.

1 格构梁计算模型

建立一个格构梁模型，如图1所示，锚杆的作用位置为支座；两锚杆之间的长度称格构梁一跨.格构梁超出最边缘锚杆部分称为悬臂段Lx.两支座之间的长度称为跨距L［5－6］.假定左悬臂段和右悬臂段长度相等，锚杆格构梁系统中的各跨跨距也相等.

图1 简化的格构梁模型示意图

图2为一个锚杆格构梁的计算模型，假定地基和格构梁都是线弹性材料，所以锚杆的锚固力与格构梁内力也是线性关系.模型参数见表1，也即格构梁的内力与表1中的7个参数有关.

图2 锚杆格构梁计算模型

表1 格构梁计算模型参数

假定锚杆预拉力为50kN，图3为格构梁弯矩分布图.从弯矩分布图可见，在支座位置有格构梁弯矩极值，在两支座之间跨中附近，也有一个极值，这些极值的大小反映了格构梁所受弯矩的大小.在工程中，一般根据这些值进行结构设计.

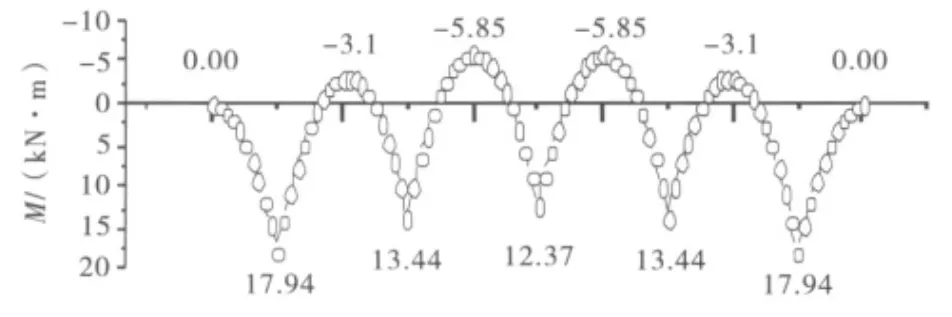
图3 格构梁弯矩分布图

地基的变形模量、格构梁的惯性矩及弹性模量是影响格构梁内力分布的重要参数.本文主要对格构锚杆系统中的地基变形模量E0、格构梁弹性模量E以及格构梁惯性矩I这3个参数对格构梁弯矩的影响进行研究.

为了研究对格构梁内力的影响，改变表1中E0、E和I 3者中的一个参数，而其他参数保持不变，观察格构梁弯矩极值与该参数的关系.

2 地基变形模量的影响

弹性地基中一个非常重要的参数就是变形模量，变形模量在岩土体中的变化范围很大，考虑到坡体表面风化破碎的岩质边坡以及土质边坡表面多为全风化碎块石以及坡积土和残积土，这些运用锚杆格构工程较多.通过类比相关工程，这些边坡表层岩土的变形模量一般在30～200MPa范围内.定义变形模量为30～200MPa，其他的参数见表1，建立数值计算模型.计算结果见表2.表2为在不同E0条件下的格构梁弯矩极值，随着地基变形模量增大，格构梁的正弯矩逐渐减小，负弯矩逐渐增大.

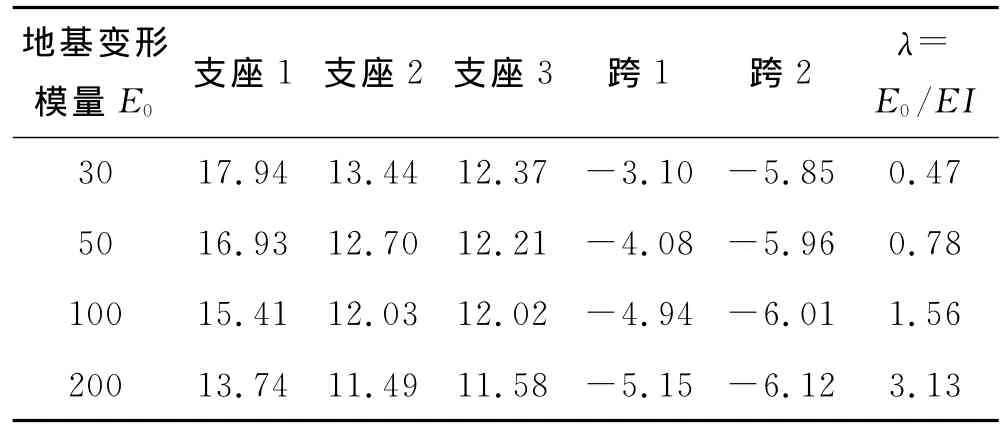
表2 不同E0条件下的格构梁弯矩极值

3 格构梁弹性模量

泊松比和弹性模量这两个参数是格构梁变形相关材料的主要参数，钢筋混凝土常用于锚杆格构梁工程中，由于混凝土等级对混凝土的泊松比的影响不大，则取μ＝0.18，根据混凝土等级按规范［14］对弹性模量进行取值.在地质灾害防治工程中，格构梁混凝土强度等级一般为C25和C30，在这里取C20～C35 4个值，建立数值计算模型，其他参数见表3.

表3 不同E条件下的格构梁弯矩极值

计算结果见表3，随着格构弹性模量的增加，格构梁的正弯矩逐渐增大，负弯矩逐渐减小.

4 格构梁惯性矩对格构梁弯矩的影响

格构梁的截面一般是矩形截面，格构梁的惯性矩主要受到格构梁截面尺寸的影响.在实际工程中，根据内力大小确定格构梁的截面，在进行设计时，一般先拟定截面的尺寸，再根据内力计算的结果来进行调整.常见的格构梁截面尺寸有0.3m×0.4m，0.4m×0.4m，0.4m×0.5m，0.4m×0.6m 不等，相应的惯性矩见表4.按以上4种截面尺寸，建立模型，其他参数见表1.经计算，格构梁内力见表4，随着格构梁惯性矩增大，格构梁正弯矩增大，负弯矩减小.

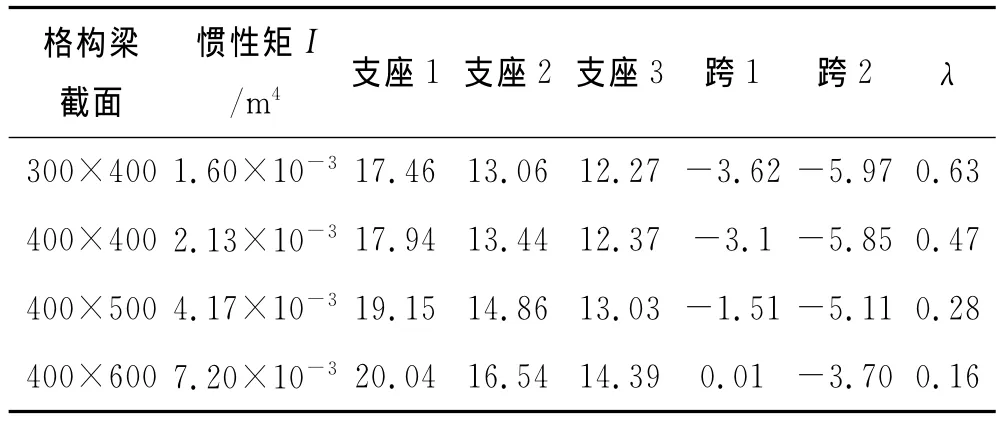
表4 不同惯性矩条件下的格构梁弯矩极值

5 相对刚度

由表2～表4可知，弯矩与λ＝E0／EI具有一一对应关系，并且随E0／EI的增大而单调减小.自然而然可以联想到，E0、I、E这3个参数影响格构梁内力的原因是这些参数变化导致E0／EI变化，而E0／EI才是影响格构梁内力分布的根本因素.EI是格构梁的线刚度，E0是地基模量，在一定程度上反映地基的刚度，记λ＝E0／EI为相对刚度.综合表2～表4中的λ的数据，发现弯矩随着λ的增大而减小，且随着λ的减小而增大.

为了证实λ是影响格构梁内力分布的基本因素这一猜测，建立若干锚杆格构梁模型，它们的地基变形模量、格构梁惯性矩、弹性模量这3个参数不同，λ相同，且其他参数均相同，比较它们的内力分布情况.按表5设计了6种组合，这些组合保证了相对刚度是相同的，而E0、I、E这3个参数至少有两个不同.其中锚杆拉力F为50kN，泊松比μ为0.3，格构梁跨距L为3m，跨数N为4，格构梁悬臂段长Lx为1.5m.