基于产业数据比对的我国经济周期波动分析

齐 爽

（吉林大学 东北亚研究院，吉林 长春 130117）

0 引言

众所周知，由于当前我国经济发展所处的阶段，我国的产业结构层次严重偏低，例如第二产业占有相当大的比重，第三产业比例偏低，而且经济增长也主要是依靠第二产业带动的，因此国民经济的稳定发展与否在很大程度上是依靠第二产业的稳定增长。而且，由于在三大产业中第二产业的投资额是最大的，因此工业经济周期波动的幅度通常都要比农业和服务业要大，极容易发生大起大落，从而引发宏观经济的剧烈波动，因此通常第二产业的波动是宏观经济波动的基础。我国第二产业的增长方式仍然比较粗放，极容易受到冲击，因此从第二产业的角度并兼以第三产业作比较来研究我国的经济周期波动，对于理解我国的行业经济波动机制、以及研究如何从产业结构的角度来调控并减缓整个宏观经济波动具有重要意义。所以本文对我国1978年以来的第二产业周期波动的特征和原因进行比较分析。

1 1949年以来，我国第二产业周期波动性历史回顾

我们先把1953年以来的工业增长率绘制于图1，它纪录了我国工业经济周期波动的历史，也记录了我国工业的繁荣与萧条。从图1可知，大致来看，我国工业增长与波动大概可分成三个阶段：即改革之前，80年代期间至90年代初期，90年代期间和加入WTO之后，总的来说，这三个阶段工业波动的平均振幅是依次递减的，总的特征是由剧烈趋向平缓。

为了进一步揭示我国工业波动的特征，接下来我们对我国工业波动的曲线进行结构分析，由于1978年是我国改革开放的起点，1992年是我国市场经济体制改革的起点，而2001年我国开始加入WTO，因此笔者猜测这三年应该是我国工业波动曲线的结构突变或结构转折点。为了对这一点进行验证，我们对1953年以来的工业增长率序列进行邹检验。

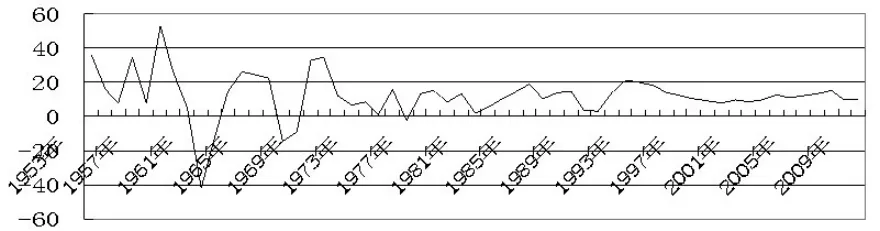
图1 我国工业总产值增长率波动曲线（%）

所谓邹检验（Chow test）是一种计量经济检验，主要是用来检验时间序列中是否存在结构性转变，它是由经济学家邹至庄创立的。邹检验的主要思想如下：

假设我们的数据模型是：

如果我们把时间序列分成两组，则：

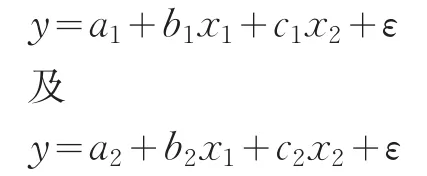
邹检验就是检验是否a1=a2，b1=b2和c1=c2。假设SC是组合时间序列的残差平方和，S1是第一组序列的残差平方和，S2是第二组序列的残差平方和。N1和N2分别是每一组时间序列的观察数目，k是参数的总数。

邹检验的检验值是：

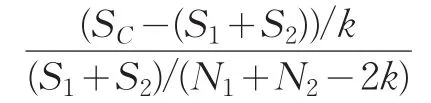
邹检验的检验值呈F-分布，它的自由度为k和N1+N2－2k。

因此邹检验的第一步是要构造一个回归方程，由于工业波动是经济波动的一部分，我们以GDP增长率（Y）为自变量、工业增长率（G）为因变量构造一个回归方程：

然后利用EVIEWS软件包估计如（2）式所示：

根据EVIEWS5.0软件包进行CHOW检验可知（如表1），当设定结构转折点为1978年、1992年和2001年时，F统计值、似然比以及WALD统计值的概率值都是零，表明这3年确是我国工业波动的结构转折点。

其次我们对我国第三产业序列也进行邹检验分析，其结果如表2所示，由表2可知，1953年以来的第三产业序列也存在与第二产业同样的三个转折点。

最后我们把工业波动按以上的CHOW检验分割的四个时期进行纵向和横向比较，结果如表3所示。从表3分析可知，从纵向来看，工业波动最突出的特征，是随着时间的推进，其波动的振幅越来越小。例如，1953～1963年期间的波动属于巨幅波动，平均振幅达到了45%；而1986～2008年期间的平均振幅只有7%；另外波长也大幅度上升了，这表明我国工业行业的波动频率大幅度下降了，可以认为，随着市场化改革的逐渐推进，我国工业的抗衰退能力大大增强。但与服务业相比较，工业下降的幅度依然不够大，改革以来工业波动振幅下降的幅度为77%，而服务业下降了将近90%。

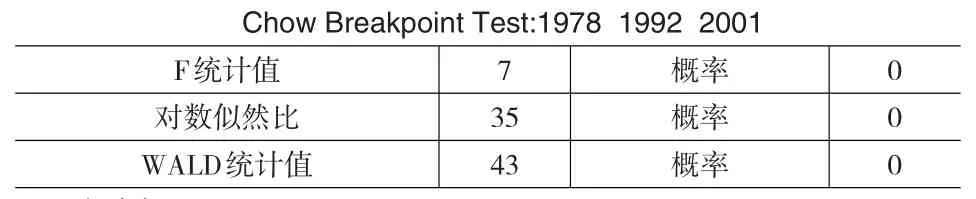
表1 1953年以来我国工业波动的结构检验

表2 1953年以来我国第三产业波动的结构检验

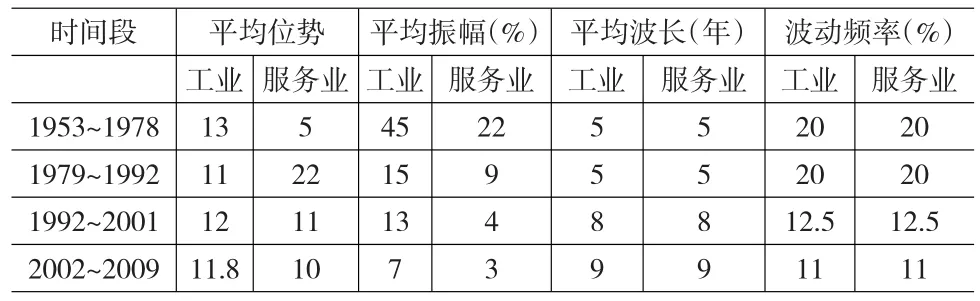
表3 我国工业及服务业波动的纵向回顾

从横向来看，我国工业波动幅度依然属于大起大落，与服务业相比，改革之前二者振幅的平均比值为1.6%，改革之后上升到了3.3%，这说明我国工业周期波动比服务业要大得多，仍然极不稳定，因此促进工业经济波动的缓和化任重道远，对国民经济的发展也意义重大。

2 基于二阶导数处理的我国第二产业周期波动性及其特征

这一部分我们利用二阶导数来分析我国工业周期波动特征，利用二阶导数处理工业波动的原理如下：

我们用kt来表示第t年的第二产业增长率，则

因此我们可以用相邻两年增长率的差来度量工业波动的振幅大小，如增长率的差的绝对值大则表明增长率变动剧烈，工业总产值振幅大，而且最重要的是表明拐点急促，经济波动的转折点剧烈，工业经济的“急刹车”和“硬着陆”特征明显。如图2是我国1954～2008年工业增长率的二阶导数处理曲线。从图2可看到，根据二阶导数的大小，我国工业波动也如同前面一样可分成三个阶段，第一阶段的二阶导数值达到近0.4，第二阶段的转折的剧烈程度稍小了一些，其绝对值一般都在0.07以下，波动转折剧烈程度最小的是第三阶段，其绝对值一般都在0附近波动，而且与GDP波动相比，第一阶段和第二阶段的二阶导数值都大于GDP的二阶导数值，尤其是第一阶段，表明这段时期的工业增长率的转折比GDP波动要剧烈得多，而第三个阶段则与GDP的二阶导数相差不大，其原因是由于前两个阶段基本上还是属于计划经济，供求矛盾突出，再加上国家对于宏观经济的调控缺乏经验，常常是大松大紧，而且工业增长又常常是先行指标，由此导致了工业经济的剧烈转折，多次出现“硬扩张”和“硬着陆”，而自从加入WTO以来，我国的市场化程度空前提高，与国际经济接轨的程度也空前提高，供需矛盾得到了极大的缓解，因此工业增长和宏观经济增长也实现了“软着陆”和“软扩张”。

图2 我国1954～2008年工业总产值与GDP总值的二阶导数处理曲线（%）

其次我们对第三产业的二阶导数处理曲线进行分析，如图3所示，我们发现，第三产业总产值的二阶导数处理曲线的振幅比GDP的二阶导数处理曲线要略低些，前者平均为5%，后者平均5.4%，这说明GDP波动的拐点比第三产业要急促，转折点也比第三产业要更加剧烈，而第三产业的“软着陆”与“软扩张”的特征比GDP要突出。

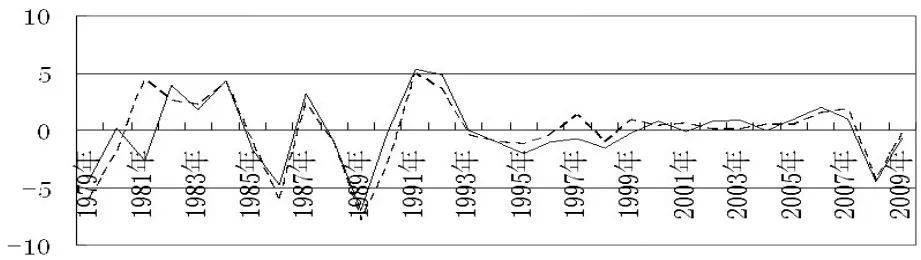
图3 GDP与第三产业的二阶导数处理曲线

因此，从以上分析可得出以下结论：即第二产业波动曲线的转折是最剧烈的，GDP次之，第三产业最小。这也说明我国第二产业对宏观调控是最敏感的。

3 我国第二产业对宏观经济冲击的杠杆效应分析

这一部分我们先把第二产业波动曲线与GDP波动曲线的拟合图绘制于图4，由图4可知，第二产业波动曲线的振幅也远远大于GDP波动的振幅，并且几乎每一轮周期的振幅都要大于GDP波动，因此我们推测第二产业比例的增大是否会加剧经济波动？这一部分我们从HP滤波和非对称效应的角度来进行验证。

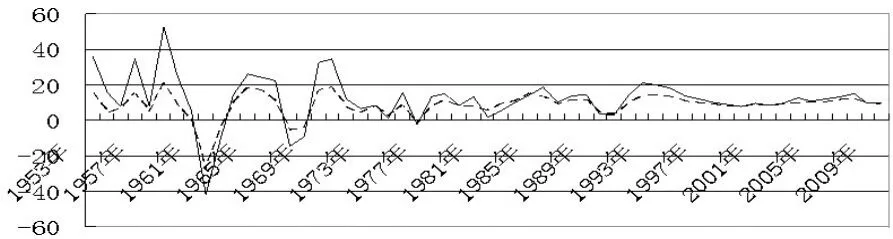
图4 第二产业波动与GDP波动曲线比较

3.1 基于HP滤波角度的我国第二产业对宏观经济冲击的杠杆效应实证检验

利用HP滤波来对二者的关系进行实证检验的基本思路是：先用HP滤波公式求出历年经济波动的振幅指标，然后再看第二产业占GDP的比值（用SY表示）与历年GDP波动的振幅的关系。而用HP滤波求历年经济波动振幅的方法是：采用HP滤波法求出我国改革以来的潜在经济增长率之后，再求出每一年的GDP增长率与潜在经济增长率的差的绝对值即是历年的振幅指标，我们用Kt表示。如图5是SYt与Kt的曲线图，由图5可知，二者总的趋势是下降，也就是说，随着第二产业比例的减小，经济波动幅度是逐渐趋向平缓的。

图5 第二产业比重与历年GDP振幅曲线比较

为了更加准确的分析二者的关系，我们再对SY与Kt的关系进行回归分析，依靠EVIEWS软件，我们可得以下回归式：

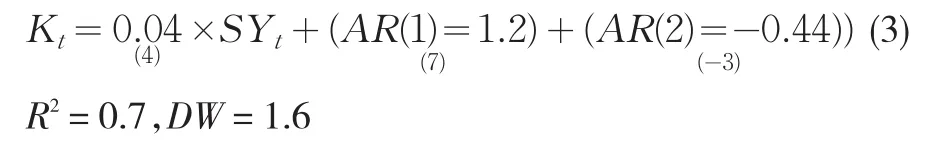
由（3）式可知，各变量拟合得很好，T统计值显著，而且（3）式表明，当其它因素不变时，第二产业比例每减少一个百分点，就会使得经济波动的振幅减少0.04%，二者的变化方向一致，这与前面的分析是一致的。

其次我们再对第三产业占GDP的比值（TY）与Kt的关系进行分析，先绘制二者的拟合曲线图如图6所示。图6中两变量的关系更加清晰，随着第三产业比例的增大，经济波动的振幅逐渐减小，经笔者通过GRANGER因果检验表示，得知前者单向作用于后者。再者，我们同样可以建立两变量的回归式如（4）式所示：

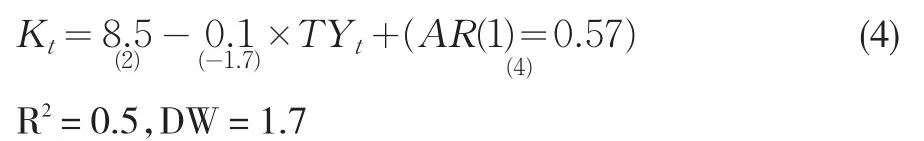
与第二产业刚好相反，（4）式表明，当第三产业比例每增加一个百分点时，会导致经济波动幅度减少0.1%，这说明第三产业对经济波动的作用与第二产业是刚好相反的。

3.2 基于非对称效应的我国第二产业对宏观经济冲击的杠杆效应分析

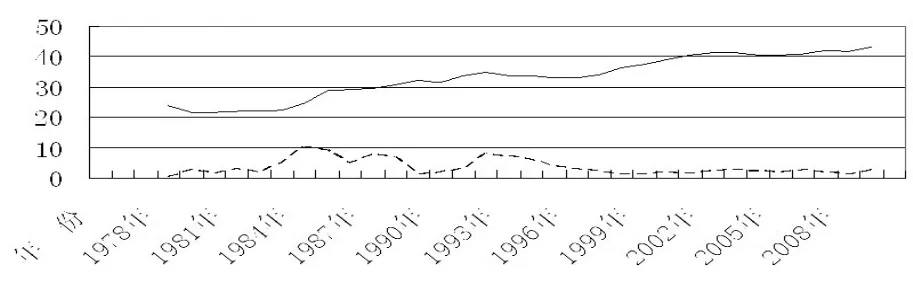
图6 第三产业比重与历年GDP振幅曲线比较

这一部分我们用TARCH模型来对第二产业对宏观经济的杠杆效应进行实证检验，所谓TARCH模型，即是指以下的均值方程与条件方差方程:

均值方程:

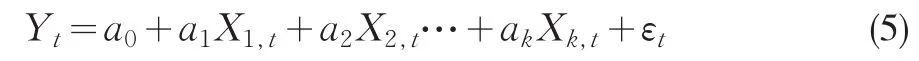
条件方差方程:

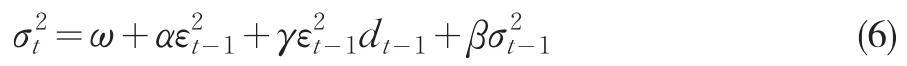
我们对工业增长率与GDP增长率构造均值方程和条件方差方程如式(7)、(8)所示：

均值方程(INDt与Yt分别为工业增长率和GDP增长率)：

条件方差方程：

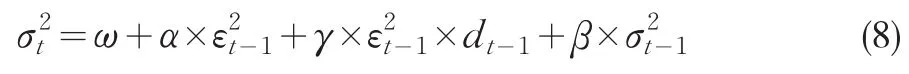
再利用EVIEWS5.0软件包，以1978～2009年上述两变量的数据作样本，可求得相应的计量经济模型如式(9)、式(10)：

均值方程：

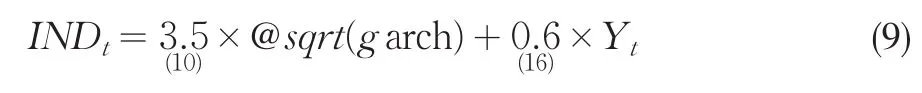
方差方程：

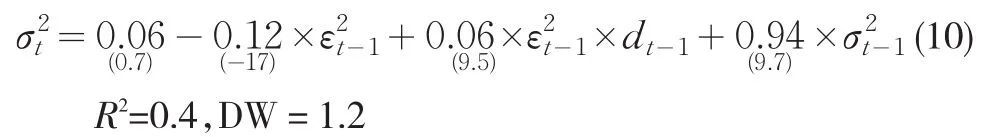
接下来我们再建立第三产业增长率（SEVt）与GDP增长率的均值方程和方差方程如（11）、（12）式：

均值方程：

方差方程：(10)

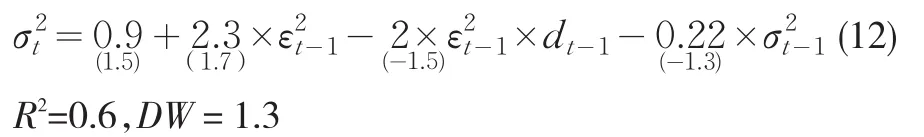
在以上各式中,各系数的T统计值都较显著，TARCH项γ的系数显著不为零，说明第二产业和第三产业都对经济波动具有非对称效应。而且第二产业方差方程中TARCH的系数γ是大于零的，这再次证明改革以来第二产业对经济波动的非对称性影响是越来越大的，同理，第三产业方差方程中的非对称项的系数是小于零的，也表明第三产业对经济波动确实具有缓和作用。

4 结论

本文以第三产业为参照，对第二产业的经济波动特征进行了分析，可得出以下几点结论：（1）通过利用邹检验方法对我国工业周期波动的分析，得知从1953年以来我国第二产业波动分别在1978年、1992年和2001年出现了结构突变，按被这三年分割的四个时期进行比较，发现工业经济波动的振幅是显著减小，另外工业波动的波长也大幅度上升了，因此随着市场化改革的逐渐推进，我国工业的抗衰退能力大大增强。但与服务业相比较，工业下降的幅度依然不够大。（2）通过对工业总产值进行二阶导数分析，得知其二阶导数值（绝对值）也是一个逐渐下降的过程，但与同时期的GDP相比，工业总产值的二阶导数值明显大于GDP，而第三产业的二阶导数值略小于GDP，因此笔者认为，第三产业波动的转折点最平缓，经济的“软扩张”和“软着陆”特征明显，而工业波动的转折点剧烈，尤其是九十年代之前，多次出现“急刹车”和“硬着陆”，这种结果比经济的大起大落对经济的冲击更大，对人民生活的福利损失也更大。（3）通过用HP滤波法对工业经济对宏观经济冲击的效果进行分析，得知随着工业占GDP比例的减小，经济波动的振幅也随之减小，而且通过用非对称性方法进行分析，得知非对称项γ的系数显著大于零，这说明工业经济对宏观经济有着杠杆冲击效应；对第三产业进行分析时刚好相反，随着第三产业占GDP比例的增加，经济波动的幅度是越来越小的，而且通过非对称性方法进行分析得知，其回归式的非对称项是小于零的，表明第三产业对经济波动确实有着缓和作用。

[1]徐敬君,刘恒.中国经济周期波动的产业结构特征[J].云南民族大学学报,2005,(3).

[2]庇古.工业波动论[M].北京：商务印书馆,1999.

[3]孙广生.经济波动与产业波动(1986—2003)——相关性、特征及推动因素的初步研究[J].中国社会科学,2006,(3).

[4]雎国余,蓝一.中国经济周期性波动微观基础的转变[J].中国社会科学,2005,(1).

[5]Baxter,M.,King,R.Measuring Business Cycle:Approximate Bandpass Filter for Economic Time Series[J].Review of Economics and Statis⁃tics,1999,(81).

[6]刘常勇，刘阳春.产业升级转型的技术与市场生命周期－以新兴经济的高科技产业为例[J].中山大学学报,2009,(1).

[7]陈浪南.我国经济周期波动的非对称性和持续性研究[J].经济研究,2007,(4).