三维双楔面定常超声速流动研究

杨 旸，滕宏辉，姜宗林

（中国科学院力学研究所高温气体动力学重点实验室，北京 100190）

0 引言

三维双楔面超声速流动是一个具有广泛应用背景的研究问题。对于超声速／高超声速飞行器，其翼身结合、垂尾／平尾夹角等处会形成复杂的三维激波／激波相互作用和激波／边界层相互作用，影响飞行器的气动性能。又如对于超燃冲压发动机三面压缩进气道，双楔面超声速流动形成的三维激波结构会导致低总压区的形成，降低进气道的总体性能。过去的几十年里，人们对于该问题给予了足够的重视并开展了较多的研究［1－7］。Charwat等［1］对该问题做出了较早的研究，并依据实验结果阐述了三维激波相互作用后形成的桥激波、透射激波等基本波系结构。Watson等［2］通过实验发现透射激波与边界层相互干扰形成的三维λ波及三维涡结构，并依此解释了壁面热流和压力的变化。Marsilio［5］对该问题中涡的不稳定性做出了数值研究，结果显示随着来流马赫数的增加，截面上的滑移线逐渐卷起形成对称结构的涡，并随着马赫数的进一步增加而失稳并不再对称。岳连捷等［6］从进气道角度研究该问题，发现激波相互作用形成的桥波区总压恢复系数较低，并研究了楔面角度变化对桥波区的影响。该双楔面超声速流动问题主要包括远离边界层近似无粘的激波／激波相互作用和粘性主导的激波／边界层相互作用两个方面，在具体研究过程中可以将其分别讨论。图1是该三维无粘流动的示意图，其中来流马赫数为M0，两个楔面的倾角和激波角分别为θ和β，前缘后掠角及双楔面间夹角分别为χ和ν。θn和βn分别为垂直于楔面前缘方向上的楔面角度和斜激波角，当后掠角χ趋于0时θn和βn分别趋于θ和β。超声速流动使得两个楔面上分别形成斜激波面i，其相互作用后在对称面反射形成规则或马赫反射。对于马赫反射，在两楔面夹角处形成桥激波m。图2为Goonko等［7］的无粘数值模拟结果中垂直于来流方向的二维截面上的激波结构。可以看到，截面中的定常激波在对称面上反射形成了过渡马赫反射和双马赫反射结构，然而这两种反射结构在二维定常激波反射中是无法形成的［8］。因此，三维双楔面超声速流动形成的激波／激波相互作用在二维截面上的定常激波反射结构无法用二维定常激波反射理论解释。之前人们的研究大多是通过实验和数值模拟得出结论，并没有从理论上分析和解释三维空间内形成这种激波结构的原因，也没有给出形成各种不同马赫反射结构的来流马赫数和楔面倾角组合范围。本文着眼于远离边界层的三维激波相互作用，通过理论分析将该三维定常激波相互作用与二维非定常激波反射建立联系，解释了二维截面上形成过渡马赫反射和双马赫反射的原因。同时，通过二维简化，利用非定常激波楔面反射理论求解得出截面上形成各种反射结构的马赫数和楔面倾角组合范围以及双楔面间夹角、前缘后掠角的影响，并通过数值模拟加以验证。

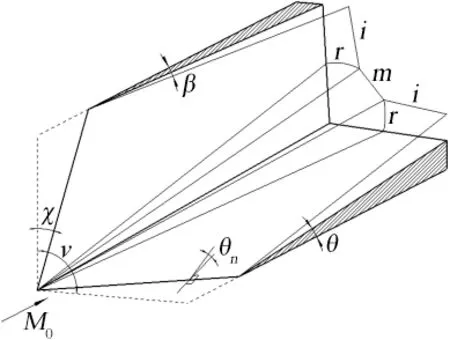
图1 三维双楔面超声速流动示意图Fig.1 Schematic of supersonic flow over 3－D intersecting wedges

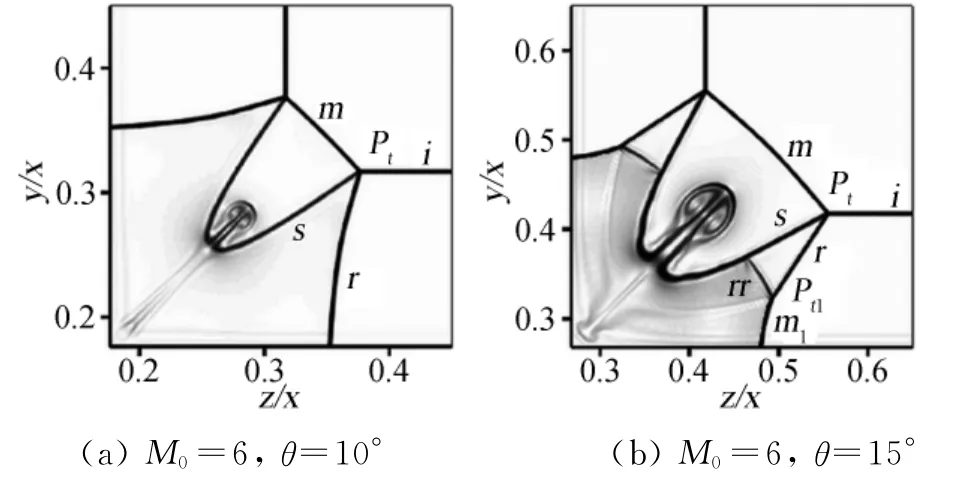
图2 二维横截面上过渡马赫反射和双马赫反射Fig.2 The transitional－Mach reflection and double－Mach reflection on 2－D cross section

1 理论分析方法

由于本文所探讨的双楔面是对称结构，因此在两楔面之间三维空间中存在有对称面，理论分析时只需考虑对称面的一侧即可。由于目前为止还没有三维激波相互作用的理论，因此该三维问题需要二维简化后才能进行理论分析。将三维激波简化到二维截面进行分析的前提是截面内的激波只具备二维特性，即在截面内二维激波前后垂直于截面的气流速度分量不因激波的存在而改变，二维激波的存在只改变了截面内平行于截面的气流速度分量。基于以上考虑，选取垂直于斜激波面i与对称面的交线AB的截面作为二维特征截面简化该三维问题，如图3 所示。图4是该特征截面的示意图，截面内激波i′前后的气流速度分别被分解为垂直于截面的速度分量和平行于截面的速度分量。若能证明激波前后垂直于截面的速度分量相等，即M0n＝M1n，则此二维简化是可行的。以下对此进行证明：

对于来流马赫数M0，前缘后掠角和双楔面间夹角分别为χ和ν的流动，来流经过斜激波面i后的速度矢量为：

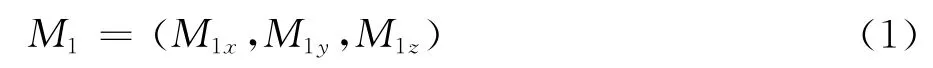
其中：

AB方向的矢量为：

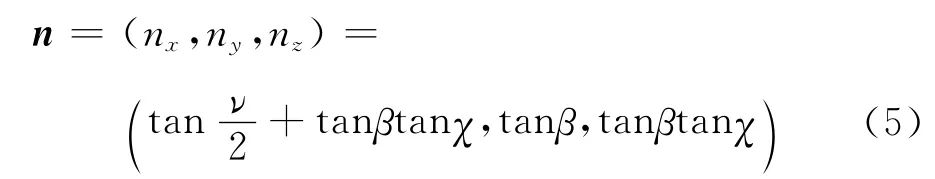
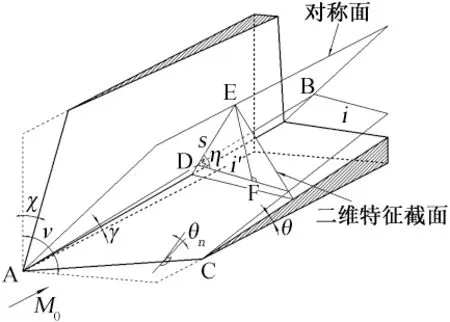
图3 理论分析方法示意图Fig.3 The schematic of theoretical analysis

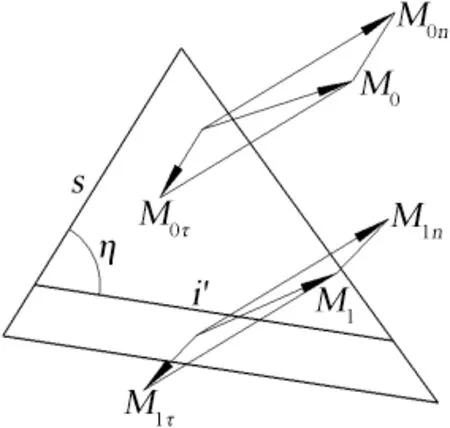
图4 二维特征截面Fig.4 The 2－D characteristic cross section

又有：

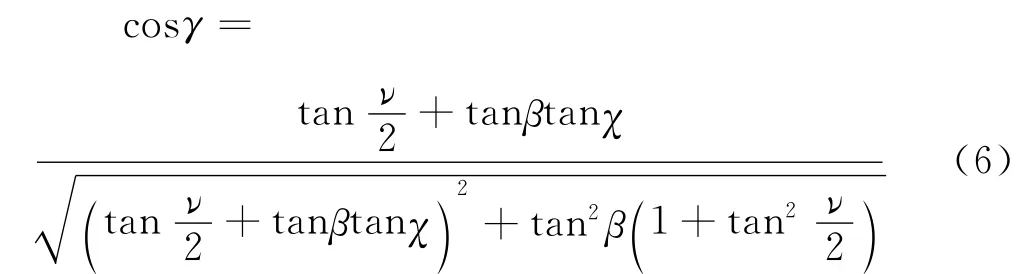
因此，可以求得M1在AB方向的投影为：

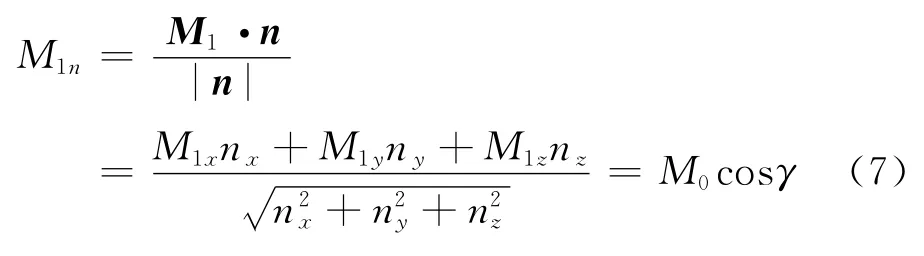
同时，不难得出M0n＝M0cosγ，由此证明了二维特征截面上激波两侧垂直于截面的气流速度分量相等，即将三维激波结构简化到该二维特征截面进行分析是正确的。

在二维特征截面内，激波i′前平行于截面的气流速度分量为：

该速度分量方向平行于二维特征截面与对称面的交线s。DF为二维特征截面内垂直于激波i′的直线，通过几何关系不难证明DF 垂直于斜激波面i。由点A、B、C的坐标可得斜激波面i及直线AB的解析式，即可通过点到平面和直线的距离公式求出EF 和DE，最终得出二维特征截面内激波i与对称面s的夹角：

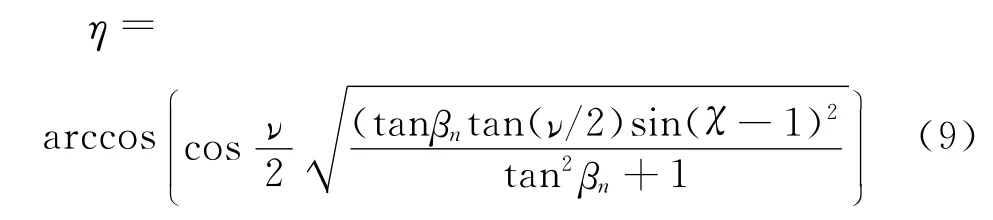
在二维特征截面内，定常激波i′静止，激波前的空气以马赫数M0τ沿二维特征截面与对称面的交线s朝着激波方向运动。通过伽利略变换，截面内激波i′前方的空气变换为静止状态，激波i′以马赫数M0τ沿着二维截面与对称面的交线s方向运动并形成反射。至此，通过伽利略变换，二维特征截面内定常激波反射问题转变为了非定常激波的楔面反射问题，如图5所示。由于在一定的激波马赫数和楔面倾角组合下非定常激波楔面反射可以形成过渡马赫反射和双马赫反射，因此二维截面内形成以上两种马赫反射结构的现象也得到了解释。同时，激波马赫数M0τ以及激波与对称面夹角 都已求得，因此可以通过二维非定常激波楔面反射的结论求解该截面内激波反射构造，并得出三维空间内激波相互作用结构。

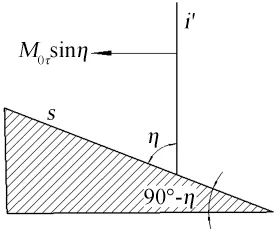
图5 伽利略变换后运动激波反射示意图Fig.5 Schematic of the pseudo－steady shock wave reflection after the Galilean transformation

2 数值模拟方法

本文研究三维空间内激波相互作用结构，粘性作用可以忽略，因此采用三维Euler方程作为控制方程。对于理想气体，直角坐标系下的控制方程可以表达为：

上述表达式中，ρ、p和E分别代表气体密度、压力和单位质量总内能，u、v和w为气体在x、y和z方向上的速度分量。单位质量总内能表达式为：

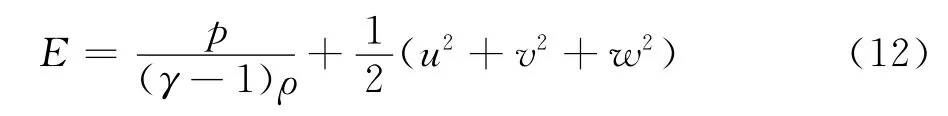
控制方程的离散为如下方程：

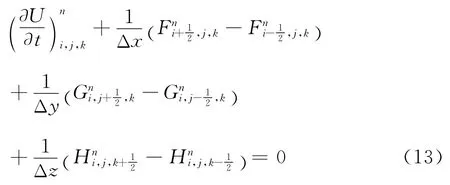
其中的对流项通量项F、G、H利用二阶NND 格式［9］求解，采用minmod函数作为限制器。计算域网格采用正交化处理后的均匀结构网格。由于采用并行程序计算，网格数达千万量级。计算域入口给定来流条件；出口边界假定沿来流方向流场参数变化很小，边界条件由外推法给出；上边界和右边界给定无反射边界条件；固壁边界采用无穿透边界条件。

3 结果与讨论

3.1 无后掠角垂直双楔面

对于两个楔面间夹角ν＝90°且后掠角χ＝0°的情况，在不同马赫数和楔面倾角的组合下，入射斜激波在对称面上反射形成各种不同的反射结构。图6为本文通过数值模拟得出的在垂直于自由来流速度方向的截面上形成的规则反射（RR）、单马赫反射（SMR）、过渡马赫反射（TMR）以及双马赫反射（DMR）结构。由于二维非定常激波楔面反射理论中弱激波反射理论尚不完善，本文中暂不考虑弱激波反射问题。对于无后掠角垂直双楔面，M0τ和η的表达式可简化为：

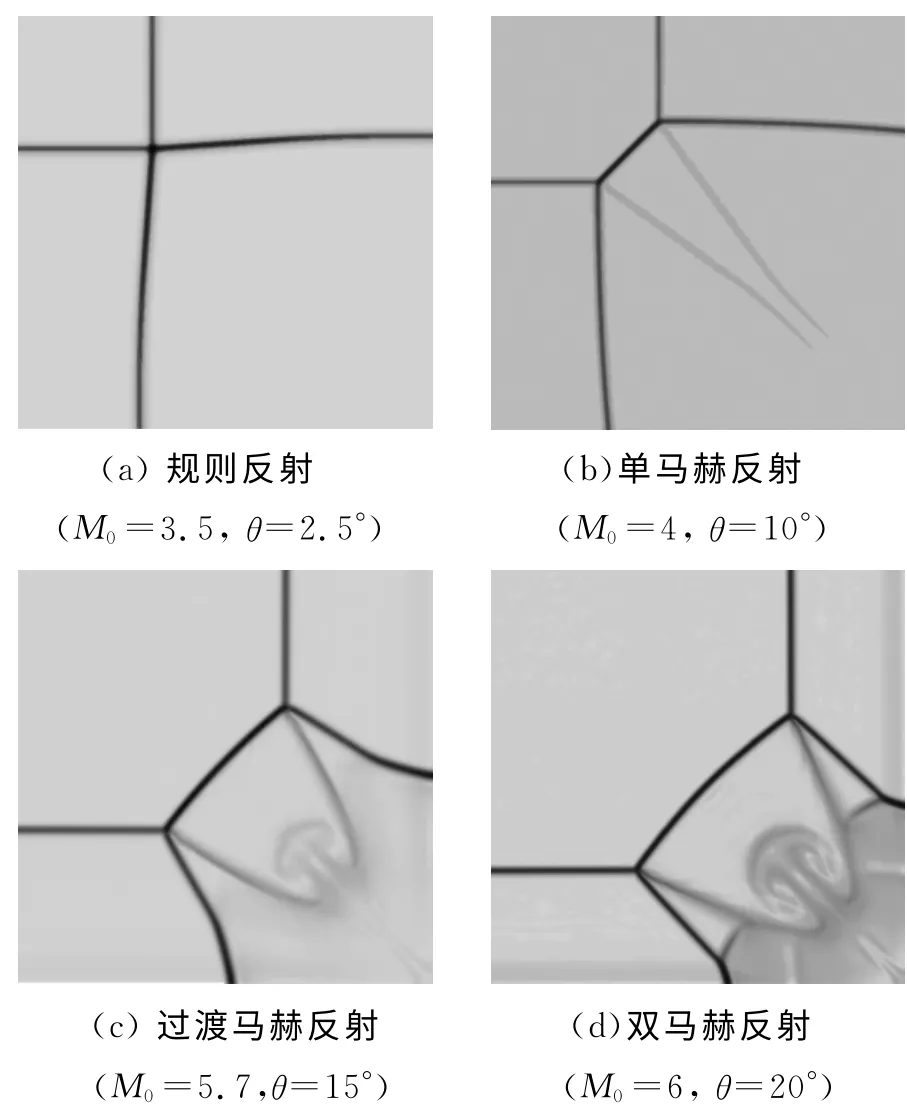
图6 截面上激波反射结构Fig.6 The shock reflection patterns on the cross section

这样，对于不同的来流马赫数以及楔面倾角所对应的激波角，M0τ和η就可以求得。通过伽利略变换，可以在二维特征截面内将定常的激波反射问题转换为以M0τsinη的马赫数运动的激波在倾角为90°－η的楔面上的反射，如图5所示。由此通过二维非定常激波反射已有的结论就可以求得二维特征截面内激波反射构造。图7为理论分析及数值验证结果，图中横坐标为自由来流马赫数，纵坐标为楔面倾角，曲线代表通过上述理论分析得出的各种激波反射结构的分界线，各图标分别代表在各马赫数和楔面倾角组合下的数值模拟结果，其中实心圆点表示在给定马赫数下由于楔面倾角过大而形成了脱体激波。可以看到，理论分析结果与数值结果吻合良好，由此可以证明通过二维简化分析该三维问题是正确的，以及通过二维非定常激波反射解释该三维激波构造是可行的。

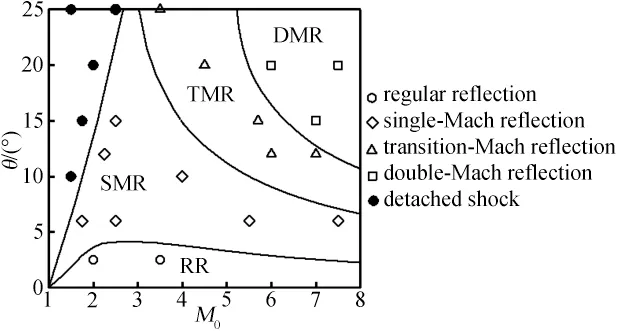
图7 不同楔面倾角和马赫数组合下截面上的激波反射结构（υ＝90°，χ＝0°）Fig.7 The shock reflection patterns on the cross section for different combinations of wedge angles and Mach numbers（υ＝90°，χ＝0°）

3.2 双楔面间夹角及前缘后掠角的影响

当两楔面间夹角ν≠90°或前缘后掠角χ≠0°时，二维截面上各种激波反射结构的形成范围与无后掠角的垂直双楔面的结果有所不同。以下分别讨论两楔面间夹角以及前缘后掠角的影响。对于ν≠90°，χ＝0°的情况，M0τ和η的表达式可简化为：

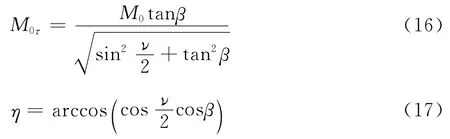
图8为通过上述理论分析所得出的两楔面间夹角对截面上激波构造的影响及数值模拟对此结果的验证。可以看到，随着两楔面间夹角的变化，二维截面上各种激波反射结构出现的范围也有所变化，即随着两楔面间夹角的减小，单马赫－过渡马赫反射以及过渡马赫－双马赫反射的分界线朝着来流小马赫数方向移动，而马赫－规则反射分界线朝大楔面倾角方向移动。注意到在图8（d）中由理论分析得出的规则反射区中出现了马赫反射的数值结果。值得注意的是，图8中的规则－马赫反射的实线分界线均是由声速准则（θS）得出的。von Neumann准则要求来流马赫数大于Mc0＝2.202，当两楔面夹角为120°和105°时各种来流马赫数和楔面倾角组合下二维截面内来流马赫数均小于Mc0，而当ν＝60°及75°时部分组合下截面内来流马赫数达到Mc0，可以得出该情况下的von Neumann准则（θN），即图8（c）、（d）中的虚线。通过数值模拟可以得出，在该虚线上下，激波结构分别呈马赫反射和规则反射结构，即此时二维定常激波反射所遵循的von Neumann准则代替声速准则成为规则－马赫反射转变的分界线。

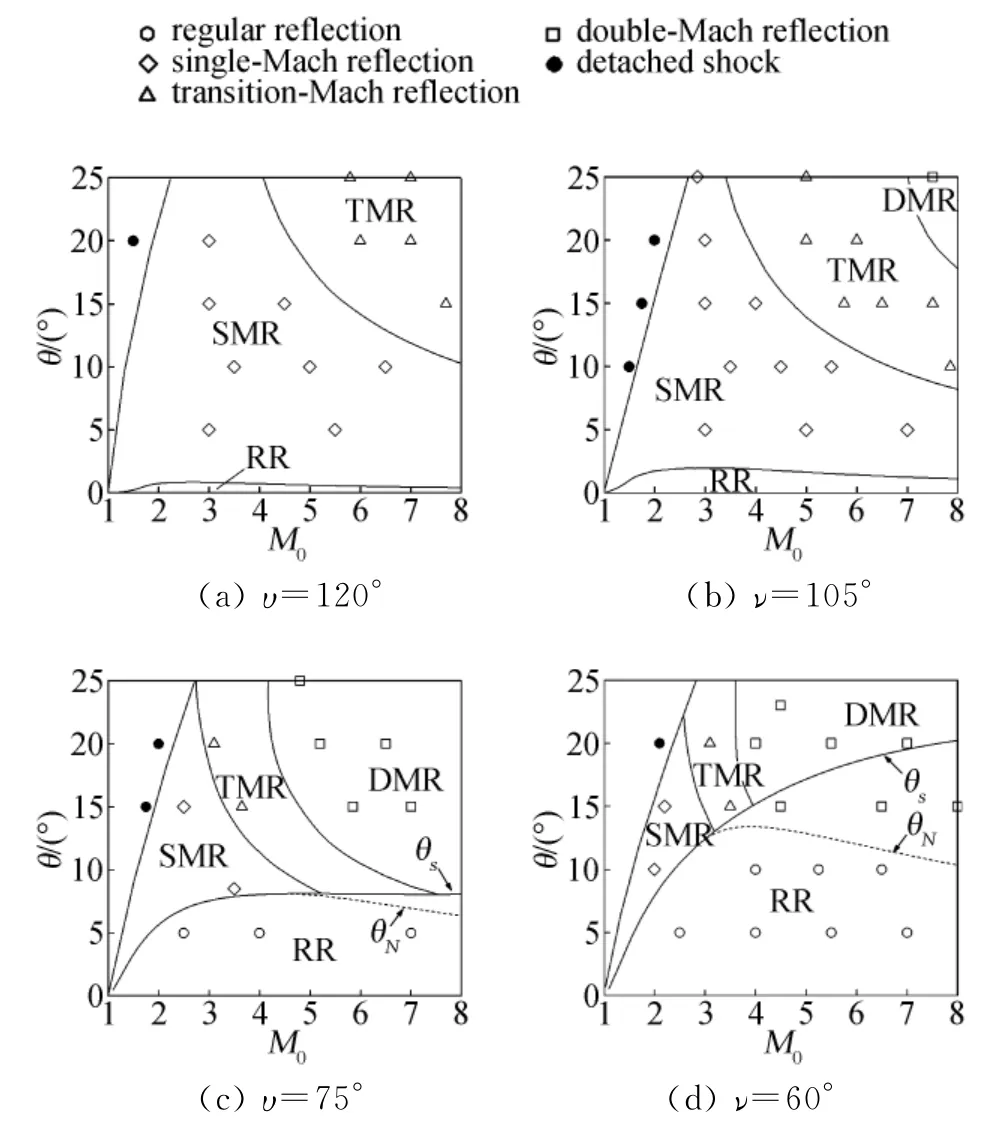
图8 不同楔面倾角和马赫数组合下截面上的激波反射结构（υ≠90°，χ＝0°）Fig.8 The shock reflection patterns on the cross sectionfor different combinations of wedge angles and Mach numbers（υ≠90°，χ＝0°）

对于ν＝90°，χ≠0°的情况，M0τ和η的表达式可简化为：

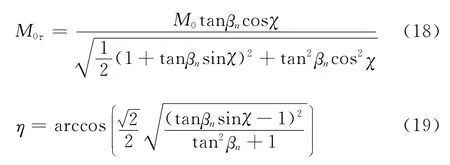
图9是通过上述理论分析所得出的前缘后掠角对截面上激波构造的影响以及数值模拟对此结果的验证。随着后掠角增大，单马赫－过渡马赫反射以及过渡马赫－双马赫反射分界线向来流高马赫数方向移动，而规则－马赫反射分界线向小楔面倾角方向移动。注意到图9的几种情况下二维截面内的激波马赫数均达不到Mc0，即不存在由von Neumann准则得出的规则－马赫反射分界线。

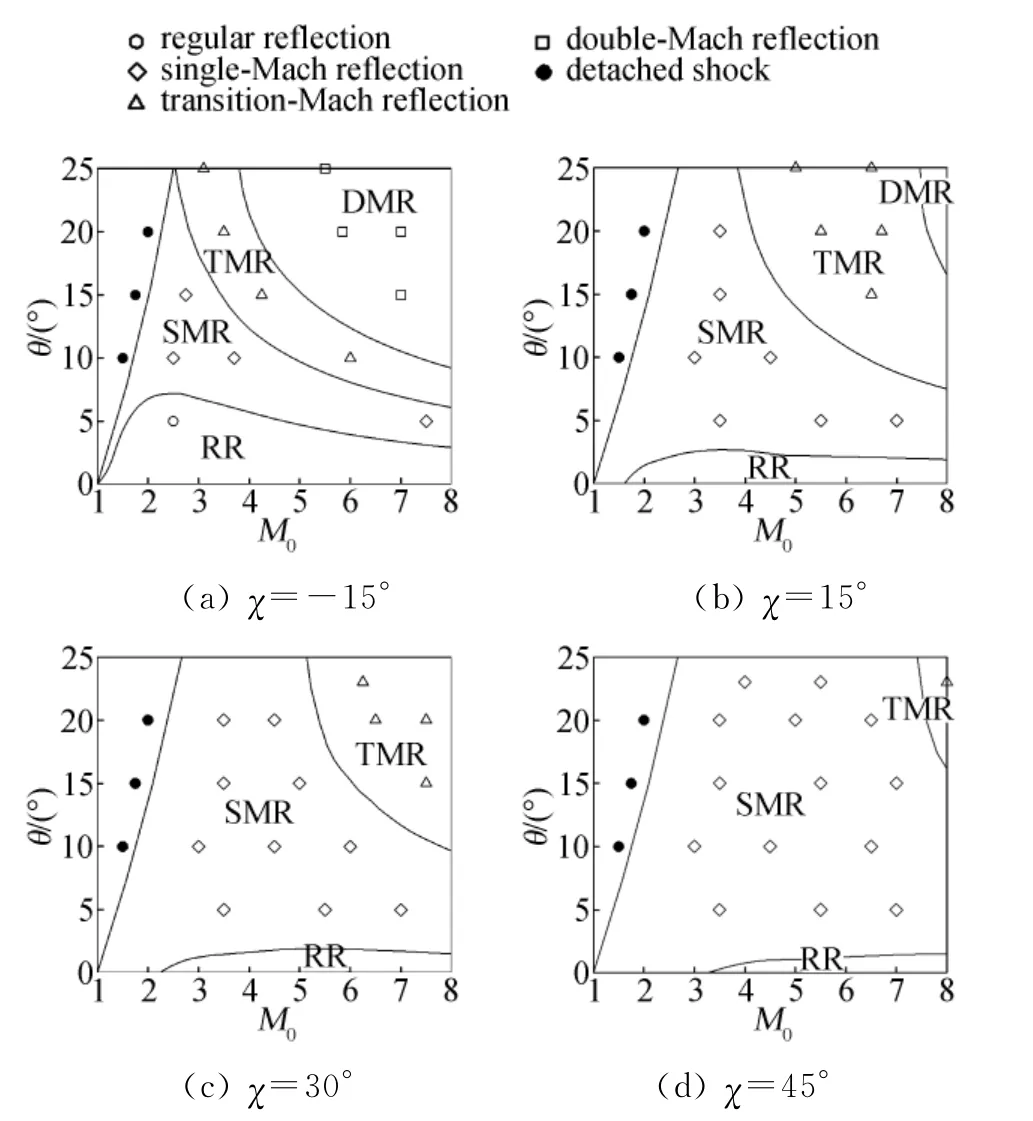
图9 不同楔面倾角和马赫数组合下截面上的激波反射结构（υ＝90°，χ≠0°）Fig.9 The shock reflection patterns on the cross section for different combinations of wedge angles and Mach numbers（υ＝90°，χ≠0°）

4 结论

本文采用理论分析和数值模拟相结合的方法，对三维双楔面超声速流动无粘激波结构做出了研究，得出以下结论：

（1）三维双楔面超声速流动形成的定常激波结构可以通过二维简化利用二维非定常激波反射理论分析得出。理论分析结果指出，入射斜激波会在对称面上反射形成规则反射、单马赫反射、过渡马赫反射以及双马赫反射等多种激波反射结构，并通过数值模拟对此结果进行了验证；

（2）通过理论分析探讨了两楔面间夹角和前缘后掠角对该激波反射结构的影响，得出了在不同双楔面夹角和后掠角下各种激波反射构造的形成范围，并分析了各种反射构造形成范围的变化趋势；

（3）在二维截面上兼有二维非定常激波和定常激波反射的特性，即形成了类似于二维非定常激波楔面反射的多种马赫反射结构，同时其规则－马赫反射转变却遵循二维定常激波反射所遵循的von Neumann准则。

［1］CHARWAT A，REDEKEOPP L.Supersonic interference flow along the corner of intersecting wedges［J］.AIAAJournal，1967，5（3）：480－488.

［2］WATSON D，WEINSTEIN M.A study of hypersonic corner flow interaction［J］.AIAAJournal，1971，9（7）：1280－1286.

［3］KUTLER P.Supersonic flow in the corner formed by two intersecting wedges［J］.AIAAJournal，1974，12（5）：577－579.

［4］MARCONI F.Supersonic，inviscid，conical corner flowfields［J］.AIAAJournal，1980，18（1）：78－84.

［5］MARSILIO R.Vortical solutions in supersonic corner flows［J］.AIAAJournal，1993，31（9）：1651－1658.

［6］岳连捷，徐显坤，张新宇，等.三面压缩进气道三维激波相干研究［A］／／中国力学学会学术大会文集［C］.郑州，2009.

［7］GOONKO Y，KUDRYAVTSEV A，CHPOUN A.3D interaction of shock waves in corner flow ［A］／／Shock Waves，Proceeding of the 24th international symposium on shock waves［C］.Beijing，2004.

［8］BEN－DOR G.Shock wave reflection phenomena［M］.New York：Springer－Verlag Inc.，1992.

［9］张涵信.无波动、无自由参数的耗散差分格式［J］.空气动力学报，1988，6（2）：143－165.