基于SST k-ω 湍流模型的平衡大气边界层模拟
2012-10-21李永乐廖海黎
胡 朋,李永乐,廖海黎
(西南交通大学桥梁工程系,四川 成都 610031)
0 引言
计算风工程(Computing Wind Engineering,简称CWE)是结构风工程中极具前景的一个方向,也是当前国际风工程研究的热点。CWE的核心内容是计算流体动力学(Computational Fluid Dynamics,简称CFD),与传统的风洞试验相比,CFD 方法具有费用低、周期短、便于模拟真实环境、描述流场细节及给出流场定量结果等优点。自20世纪60年代兴起以来,随着数值求解方法的发展和计算机硬件技术的进步,CFD 在结构风工程中的应用越来越广泛。
由于结构风工程研究的对象位于大气边界层内,研究的重点是钝体绕流,其流动可视为低速、不可压缩粘性流体的湍流运动,因此准确模拟大气边界层内的湍流流动是精确预测结构风荷载的前提,这在CFD 数值模拟中就首先要求其满足水平均匀性[1]的条件,即在没有任何障碍物的简单边界层流动下,数值模拟区域内的平均风剖面和湍流风剖面自入口到出口保持不变,这种满足水平均匀性条件的边界层称为平衡大气边界层,边界层内流场的水平均匀性程度直接影响数值模拟的精度。Blocken等[2]采用k-ε湍流模型模拟了两平行建筑物内的风速分布情况并与相应的风洞试验作对比,结果表明两建筑物中心线上行人高度处风速放大系数的计算值与试验值相差达15%左右,其原因主要是由于入口处的风速剖面在流动过程中发生了改变,即不满足水平均匀性条件,从而使计算风速放大系数的参考风速发生了变化,当根据风速剖面变化对参考风速进行修正后,风速放大系数的计算值与试验值吻合较好,文中还建议在进行数值模拟之前,应首先对无模型的空流场进行水平均匀性检验。严格说来,当且仅当计算区域入口处的来流边界条件与湍流模型(包括壁面函数)及地表粗糙特性相协调时,才能得到水平均匀性的平衡大气边界层[3],但由于湍流的复杂性,在数值模拟中精确实现平衡大气边界层常存在困难。Richards和Hoxey[1]基于k-ε湍流模型提出了满足平衡大气边界层的几个原则,给出了一组来流边界条件,并对湍流模型参数的取值进行了探讨,但文中所给出的湍动能边界条件为一常数,这与实测结果及试验结果不符。张建和杨庆山[4]基于标准k-ε湍流模型,将近壁区第一层网格的湍流量进行平均处理并施加剪切应力,从而使边界层内沿流场不同位置处的流动特征量吻合程度较高。方平治等[5]通过修正的壁面函数并采用k-ε湍流模型对平衡大气边界层进行了研究,研究结果表明修正的壁面函数对粗糙度较大的风场效果较好。Yang等[6]从标准k-ε湍流模型方程出发,假设湍流在整个边界层内处于平衡态,推导出一组随高度变化的来流边界条件,并以风洞试验数据为参考,通过改变湍流模型参数,并考虑壁面粗糙度,较好地实现了边界层流场的平衡,并将上述方法应用于SSTk-ω湍流模型[7],但已有试验表明,湍流能量仅在边界层的内层范围内才处于平衡[8-9],并且湍流模型中的参数也是根据渐近性原则通过试验确定[10]。已有研究多数是针对两方程湍流模型中的k-ε模型,结构风工程研究中SSTk-ω两方程湍流模型对钝体分离流适用性较好,应用范围较广,但针对基于SSTk-ω湍流模型的平衡大气边界层的研究较为少见。
与已有的平衡大气边界层模拟方法不同,本文通过在湍流模型输送方程中添加源项的方法使来流边界条件与湍流模型相协调,从而实现CFD 分析中空流场大气边界层的平衡。研究中首先基于SSTk-ω湍流模型依次确定出平均速度剖面、湍动能剖面,并根据剪切应力为常量确定出比耗散率剖面,再通过湍动能与比耗散率输送方程的平衡推导出源项的表达形式,最后通过相应的CFD 数值算例分别考察了不考虑源项与考虑源项时沿流场不同位置处的平均速度、湍动能及比耗散率剖面的一致性,验证了本文方法的有效性。
1 SST k-ω 湍流模型
剪切应力输送(Shear-Stress Transport,简称SST)k-ω湍流模型由Menter提出[11],该模型综合了k-ω模型在近壁区计算的优点和k-ε模型在远场计算的优点,增加了交叉扩散项,并在湍流粘性系数的定义中考虑了湍流剪切应力的输送过程,从而使SSTk-ω湍流模型应用范围更广。已有研究表明[12-13],SSTk-ω湍流模型较传统的k-ε湍流模型要更适用于具有逆压梯度流动或分离流动的计算,因而前者更广泛地应用于大气边界层钝体绕流的计算中。以张量形式表达的SSTk-ω湍流模型的流场输送方程为:
式中Γ、Γk、Γω为速度u(v或w)、湍动能k及比耗散率ω的有效扩散系数,其各自定义为:

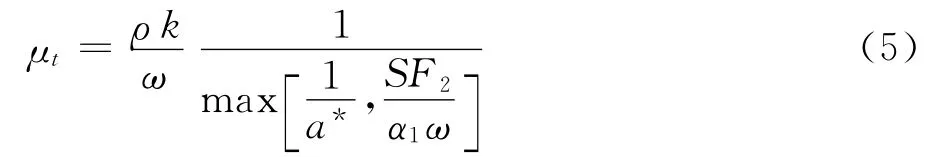
μt为湍流粘性系数,其定义为:为k、ω的产生项,Yk、Yω为k、ω的耗散项,Dω为交叉扩散项,各项分别定义为:
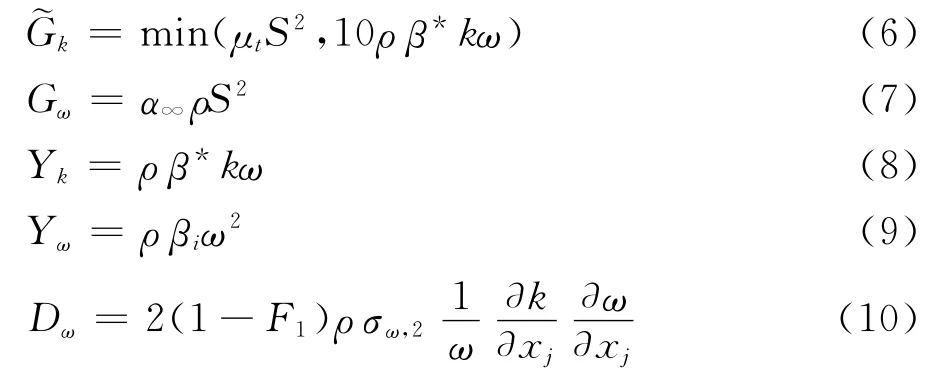
式(1)~式(10)中,ρ为空气密度,p为压强;μ为分子粘性系数,S为平均应变率的张量模量;F1、F2为混合函数;σk、σω、α*、α∞、β*及βi为湍流模型中的系数;σω,2、α1为湍流模型常数;Si、Sk及Sω为各输送方程的自定义源项,各项定义详见文献[14]。
对于SSTk-ω湍流模型模拟二维、定常、不可压缩流动的平衡大气边界层,一般要满足以下条件[1]:
(1)竖向速度v为零;
(2)压强p为常数;
(3)剪切应力τ为常数;
(4)湍动能k与比耗散率ω满足各自的输送方程。
由以上条件并考虑到μ≪μt[1,14],由此可将流场输送方程式(1)-(3)化简可得:
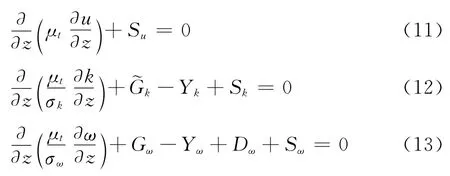
2 边界条件的确定
2.1 平均风速边界条件[15]
若将大气边界层分为满足“壁面定律”的近地层及满足“速度亏损律”的外层两部分,当存在某一重合区域使两种定律都成立时,可得到对数律的风剖面表达式:

式中u(z)为不同高度处的平均风速,u*为摩擦速度,Κ为卡门常数,取Κ=0.42,z0为粗糙长度。一般认为,对数律表示大气底层的风剖面比较理想,当为强风时适用范围可更高。为考虑地面处z=0m 时的速度,可将上式改写为:
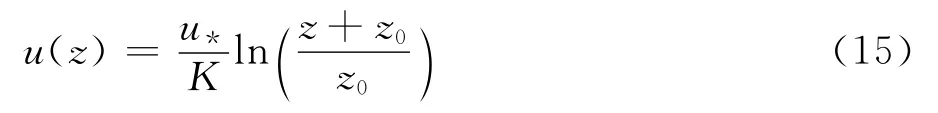
2.2 湍流边界条件
FLUENT[14]为SSTk-ω湍流模型提供了多组湍流边界条件形式,本文采用经常使用的湍动能k与比耗散率ω的一组湍流参数。对于湍动能k剖面目前没有统一的表达形式,较多地采用包含湍流强度Iu(z)与速度u(z)形如k=Ck[Iu(z)·u(z)]2的湍动能剖面形 式(其 中Ck为一常数)[2,16-18],部分采用湍动能平衡假设而确定的湍动能剖面[4,6-7],还有采用沿高 度 为 常数的湍动能剖面[1,19-20]等。考虑到湍动能始终大于零,且湍动能的表达式常含u(z)2的因子,并注意到式(15),由此本文将湍动能剖面近似地表示为:
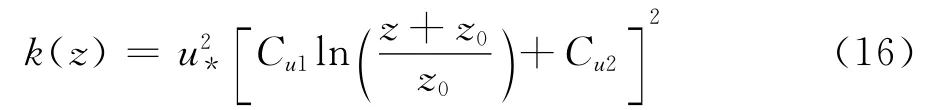
其中Cu1、Cu2为湍流边界条件参数,可由试验数据拟合得到,其它参数意义同前。
对于比耗散率ω的剖面形式目前研究较少。由上文的条件(3):“剪切应力τ为常数”,则要求τ满足:
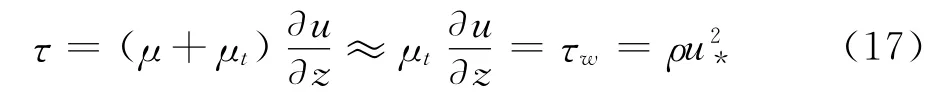
其中τw为壁面剪切应力,由此可知当且仅当Su=0时式(11)才 成立。对于式(5)μt表达式中的可视为一系数,为简化μt的形式并便于后续公式的推导,在此先近似地定义湍流粘性系数为:

将式(15)、式(18)代入式(17)可得:

注意到式(16),由此可得比耗散率ω的剖面形式为:
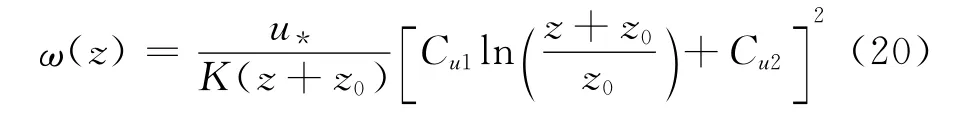
3 源项的确定
与已有的平衡大气边界层模拟方法不同,本文通过在流场输送方程式(11)~(13)中添加源项的方法使来流边界条件与湍流模型相协调。由于Su=0,以下着重考虑源项Sk及Sω的表达形式。
3.1 源项Sk 的表达形式
对于输送方程式(12)左端第一项,由式(16)、式(18)及式(19)并根据函数积的求导法则可知:
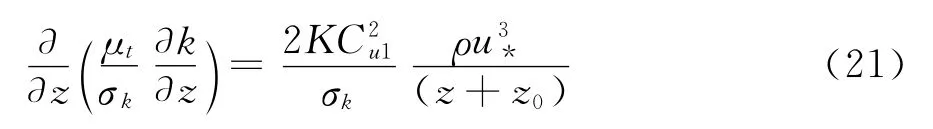
对于式(12)左端第三项Yk,由式(8)、式(16)及式(20)可知:
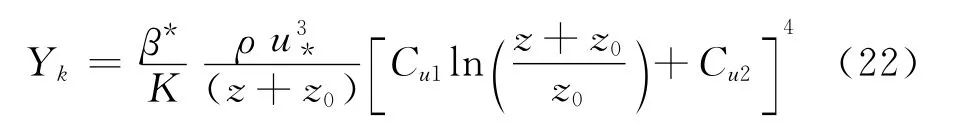

其表达式形式与式(21)相似,而10ρβ*kω的表达式与式(22)相似。由此可知,当项相叠加时,可将合并到这两项之中,考虑方程式(12)成立,由此可得源项Sk的表达形式为:
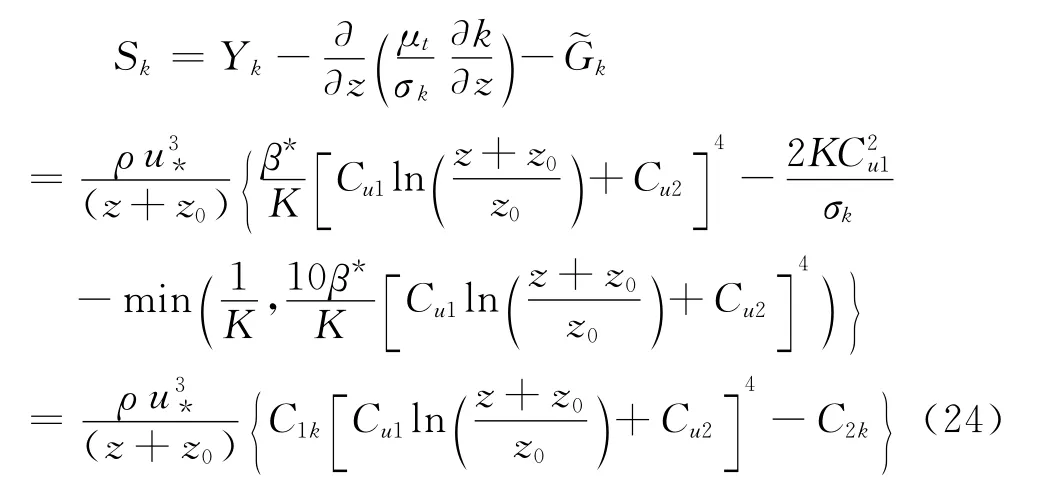
式中引入两个综合系数C1k、C2k,其中C1k为考虑系数β*/Κ及-10β*/Κ,C2k为考虑系数及1/Κ,通过对项的合并处理大大简化了Sk的形式。
3.2 源项Sω 的表达形式
源项Sω的确定方法与源项Sk的方法类似。对于方程式(13)左端第一项由式(18)、(19)及(20)并根据函数积的求导法则可知:
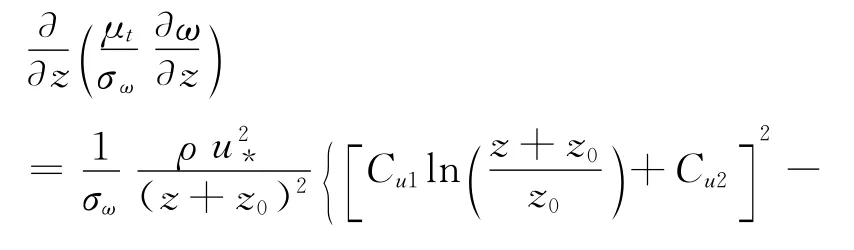
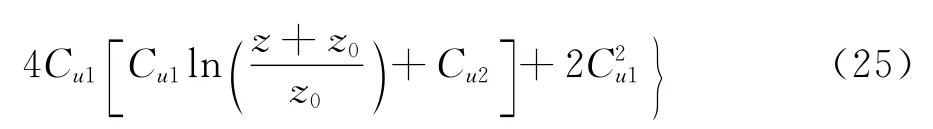
对于式(13)左端第二项Gω,由(7)、式(15)可知:

对于式(13)左端第三项Yω,由式(9)、式(20)可知:
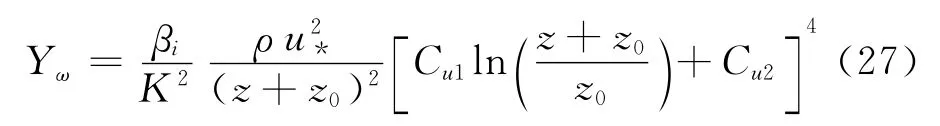
对于式(13)左端第四项Dω,由式(10)、式(16)及式(20),并注意到k与ω仅为z的函数可知:
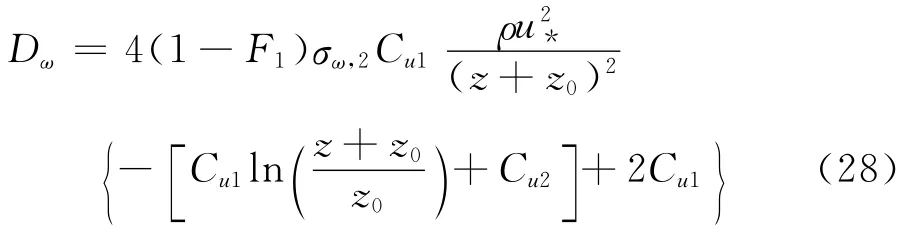
由方程式(13)成立,由此可得源项Sω的表达形式为:
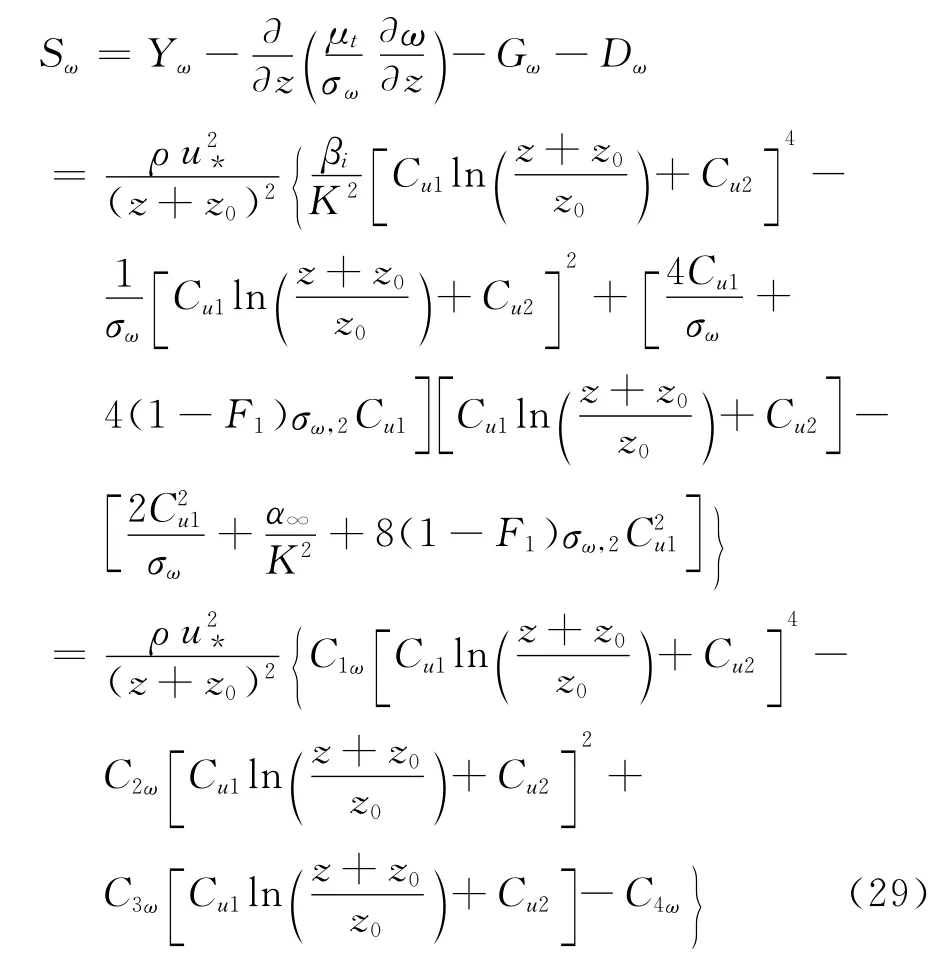
同理上式中也引入了四个综合系数C1ω、C2ω、C3ω及C4ω,这四个综合系数分别与原位置未简化的系数项相对应。
由于SSTk-ω湍流模型中各系数定义的复杂性,加之源项Sk、Sω均是基于简化的湍流粘性系数推导而成,因此上述综合系数C1k、C2k与C1ω、C2ω、C3ω及C4ω的表达形式可能比式(24)、式(29)中对应的未简化的系数项要复杂得多。为弱化湍流模型系数及对各综合系数具体形式的影响,并方便源项的应用,在此假设上述6个综合系数均为常数。需要指出的是,由于SSTk-ω湍流模型的复杂性,即使在假设上述综合系数均为常数的情况下也很难确定各系数的值,但注意到式(29)中简化后的源项Sω中第一项为正,第二项与第四项均为负,而第三项的正负号则与参数Cu1及Cu2的取值有关,可认为第二项与第四项对流场的影响相似,若第三项也为正,同理可认为第一项与第三项对流场的影响也相似;另一方面,考虑到湍流封闭方程的构造中通常假设湍动能耗散相关项与湍动能方程中的对应项有相同的机制和公式[10],对于SSTk-ω湍流模型则有:

其中f(ω)是比耗散率ω的相关项(如产生项、耗散项等;对于k-ε湍流模型,式中比耗散率ω则变为耗散率ε),而f(k)是对应的湍动能相关项,Cω是系数。若将上述思想引入到源项Sk及Sω的表达式中,则由式(24)可知:式(29)中Sω的表达式中没有第二项及第三项。基于以上分析,假设式(29)中第二项与第三项对流场的作用可被其它两项代替,于是可令简化后的Sω表达式中第二项与第三项的系数C2ω=C3ω=0,由此就减少了未知参数,同时也简化了Sω的表达形式。而对于Sk、Sω中剩余的综合系数C1k、C2k与C1ω、C4ω,通过初步试算发现C1k与C1ω对流场水平均匀性的敏感性较强,而C2k与C4ω对流场水平均匀性的敏感性相对较弱,由此可先大致确定出C1k与C1ω的值,然后再确定出C2k与C4ω的值,最后再对各系数进行局部调整就可得到基本满足水平均匀性的平衡大气边界层。
4 平衡大气边界层数值模拟验证
根据上述分析,以下从数值模拟的角度来说明在湍流模型输送方程中添加源项以实现平衡大气边界层的有效性。
4.1 数值计算模型
采用CFD 商业软件FLUENT[14]对二维的空流场进行数值模拟分析,计算区域尺寸设定为12.0m×1.8m(x×z)(对于三维区域流动,由于侧面常设置为对称边界条件,相当于二维区域流动),区域中没有放置任何物体。采用结构化网格对计算区域进行离散,最小网格尺寸zmin为0.01m,最终划分的四边形网格总数为8000个,计算区域网格划分如图1所示(纵向为x轴,竖向为z轴)。流动设为二维不可缩的定常流动,计算模型采用SSTk-ω湍流模型,计算区域各边界条件的定义如表1所示,其中入口处边界条件表达式中的各参数均通过风洞试验数据拟合得到[6]。此外,为说明源项Sk、Sω对实现平衡大气边界层的有效性,在流场的k、ω输送方程中分不考虑源项和考虑源项两种情况,不考虑源项时各综合系数均取零值;考虑源项时,源项中各综合系数值根据上文方法最终确定情况如表2所示。

表1 计算区域边界条件Table 1 Boundary conditions of the computational domain

表2 输送方程源项Table 2 Source terms of transport equations
对于求解控制参数的设置,压力与速度耦合采用SIMPLEC算法,动量方程、湍动能及比耗散率输送方程均采用二阶离散格式,使用入口处来流边界条件各特征量对流场进行初始化,残差收敛精度均设置为1.0×10-6。

图1 计算区域网格划分示意Fig.1 Schematic diagram of mesh arrangement
4.2 数值模拟结果
当不考虑源项Sk、Sω时,流场收敛后提取沿流场纵向x=-6m(入口处)、x=-2m(靠近入口的1/3 总长处,也是模型常放置的地方)、x=2m 及x=6m(出口处)处的平均速度u、湍动能k及比耗散率ω的剖面如图2所示,由图可知,各处的速度剖面及比耗散率剖面总体上能保持一致,但入口处的湍动能剖面与其它位置的湍动能剖面差异明显,表明此时的流场尚未达到平衡。而考虑源项时对应位置的各特征量剖面如图3所示,由图可知,各处的速度剖面、湍动能剖面及比耗散率剖面均有较高程度的一致性,表明此时的流场基本达到了平衡,较好地实现了平衡大气边界层。此外,对比图2(a)与图3(a)中的速度剖面可知,图2(a)顶端处速度剖面的一致性较图3(a)中的要稍差一些,同样对于图2(c)中比耗散率剖面在高度较低时其剖面的一致性也稍差于图3(c)的。通过上述无源项与有源项时流场特征量剖面的对比表明,在湍流模型输送方程中添加源项能较有效地实现大气边界层的平衡。
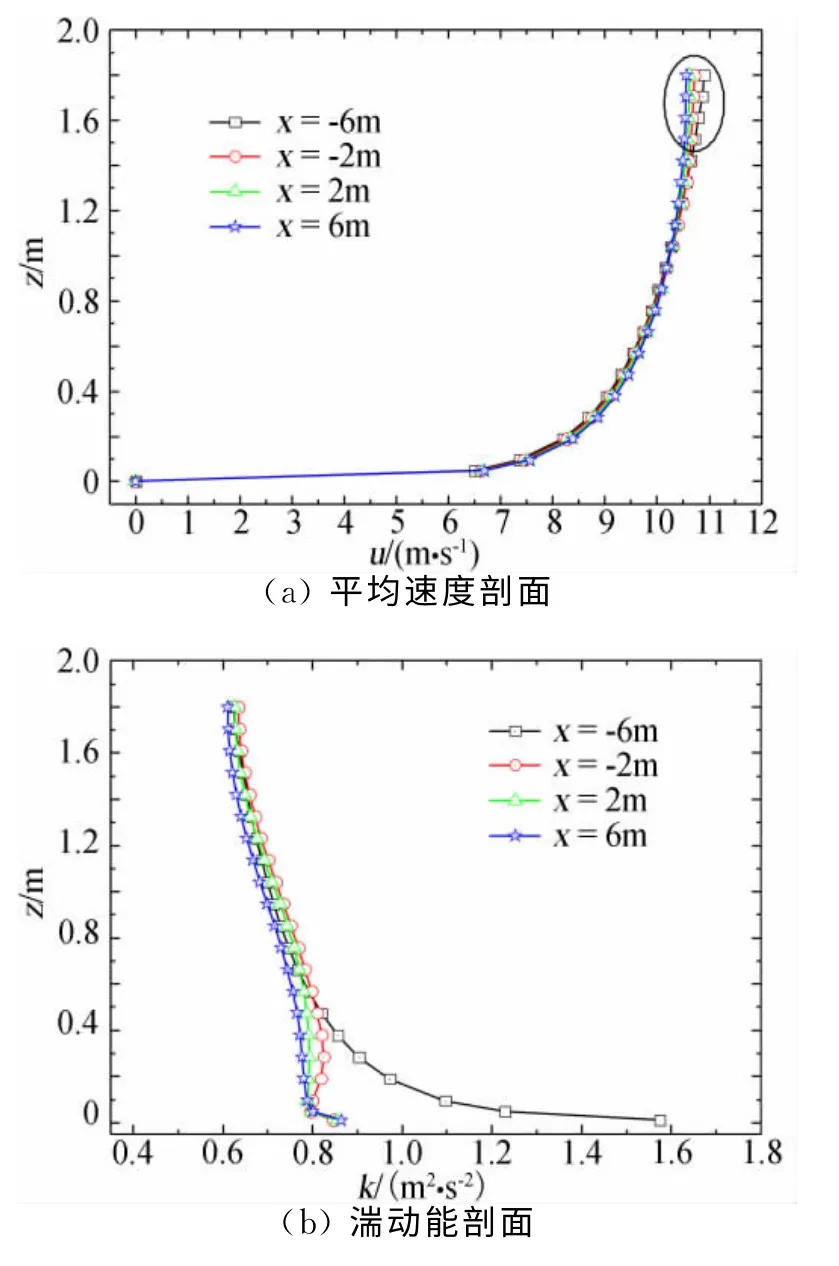
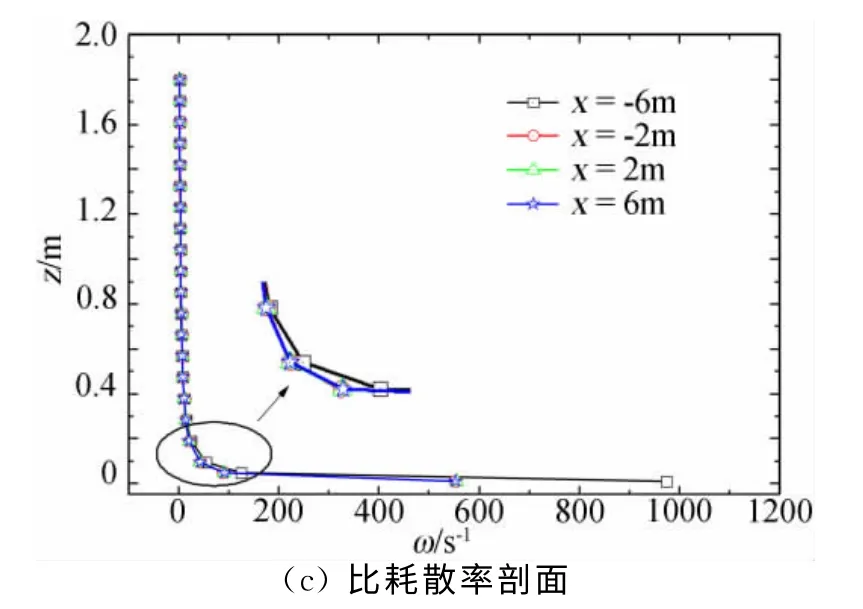
图2 不考虑源项时不同位置的平均速度剖面及湍流特征剖面Fig.2 Profiles of average wind and turbulence wind at different positions without considering the source terms
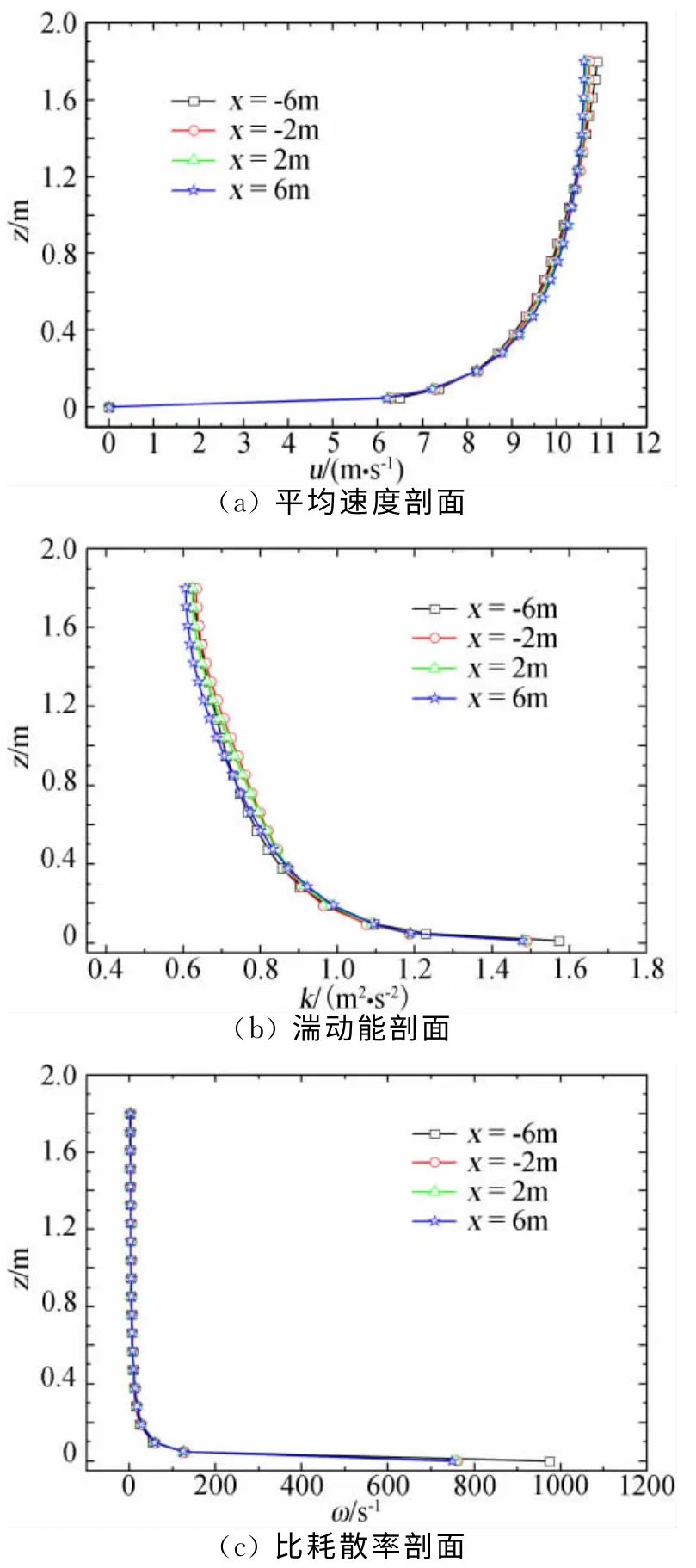
图3 考虑源项时不同位置的平均速度剖面及湍流特征剖面Fig.3 Profiles of average wind and turbulence wind at different positions with considering the source terms
5 结论
实现平衡大气边界层是进行数值模拟的前提,满足平衡大气边界层的流场能显著提高数值计算结果的精度[7]。本文基于SSTk-ω湍流模型,提出通过在湍动能与比耗散率输送方程中添加源项的方法使来流边界条件与湍流模型相协调,从而实现CFD 分析中空流场大气边界层的平衡。CFD 数值算例表明在湍流模型输送方程中考虑源项能较好地实现大气边界层的平衡,验证了本文方法的有效性。本文提出的方法虽然仅针对SSTk-ω湍流模型,但从方法实现的过程来看,同样适用于标准k-ω及k-ε系列等两方程湍流模型,具有一定的普遍性。本研究为平衡大气边界层的研究提供了新的思路和研究方法,对结构风工程中CFD 数值模拟有一定的理论及应用价值。
[1]RICHARDS P J,HOXEY R P.Appropriate boundary conditions for computational wind engineering models using thek-εmodel[J].JournalofWindEngineering andIndustrialAerodynamics,1993,46-47:145-153.
[2]BLOCKEN B,CARMELIET J,STATHOPOULOS T.CFD evaluation of wind speed conditions in passages between parallel buildings-effect of wall-function roughness modifications for the atmospheric boundary layer flow[J].JournalofWindEngineeringandIndustrial Aerodynamics,2007,95(9-11):941-962.
[3]BLOCKEN B,STATHOPOULOS T,CARMELIET J.CFD simulation of the atmospheric boundary layer:wall function problems[J].AtmosphericEnvironment,2007,41(2):238-252.
[4]张建,杨庆山.基于标准k-ε模型的平衡大气边界层模拟[J].空气动力学学报,2009,27(6):729-735.
[5]方平治,顾明,谈建国.计算风工程中基于k-ε系列湍流模型的数值风场[J].水动力学研究与进展,2010,25(4):475-483.
[6]YANG Y,GU M,CHEN S Q,et al.New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J].JournalofWindEngineeringandIndustrial Aerodynamics,2009,97(2):88-95.
[7]YANG W,QUAN Y,JIN X Y,et al.Influences of equilibrium atmosphere boundary layer and turbulence parameter on wind loads of low-rise building[J].JournalofWindEngineeringandIndustrialAerodynamics,2008,96(10-11):2080-2092.
[8]陈懋章.粘性流体动力学基础[M].北京:高等教育出版社,2002.
[9]是勋刚.湍流[M].天津:天津大学出版社,1994.
[10]张兆顺.湍流[M].北京:国防工业出版社,2002.
[11]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAAJournal,1994,32(8):1598-1605.
[12]LOUREIRO J B R,ALHO A T P,SILVA FREIRE A P.The numerical computation of near-wall turbulent flow over a steep hill[J].JournalofWindEngineering andIndustrialAerodynamics,2008,96(5):540-561.
[13]EI-BEHERY S M,HAMED M H.A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser[J].Computers& Fluids,2011,44(1):248-257.
[14]FLUENT.Fluent 6.3user's guide[M].Labnon,New Hampshire.Fluent Inc.,2006.
[15]SIMIU E,SCANLAN R H.Wind effects on structures:fundamentals and applications to design[M].USA:Wiley,1996.
[16]LAKEHAL D.Application of thek-εmodel to flow over a building placed in different roughness sublayers[J].JournalofWindEngineeringandIndustrialAerodynamics,1998,73(1):59-77.
[17]SAGRADO A P G,BEECK J V,RAMBAUD P,et al.Numerical and experimental modelling of pollutant dispersion in a street canyon[J].JournalofWindEngineeringandIndustrialAerodynamics,2002,90(4-5):321-339.
[18]GAO Y,CHOW W K.Numerical studies on air flow around a cube[J].JournalofWindEngineeringand IndustrialAerodynamics,1995,93(2):115-135.
[19]PASLEY H,CLARK C.Computational fluid dynamics study of flow around floating-roof oil storage tanks[J].JournalofWindEngineeringandIndustrialAerodynamics,2000,86(1):37-54.
[20]HARGREAVES D M,WRIGHT N G.On the use of thek-εmodel in commercial CFD software to model the neutral atmospheric boundary layer[J].Journalof WindEngineeringandIndustrialAerodynamics,2007,95(5):355-369.
