阵列误差对Capon波束形成算法的影响分析

邓志鑫

(河北省卫星导航技术与装备工程技术研究中心，河北石家庄 050002)

0 引言

标准的Capon波束形成器［1］在期望信号导向矢量精确已知时，可以获得良好的干扰抑制性能。在实际中，由于受天线误差的影响，期望信号的阵列流型并不能精确已知，这时Capon波束形成的性能会急剧下降。虽然目前已经提出许多方法来改进Capon波束形成的稳健性［2-6］，但这些算法计算复杂，会增加系统的小型化难度。随着阵列天线制造工艺水平的提高，对阵列天线的制造提出合适的指标以保证Capon波束形成算法的性能是解决阵列误差问题的有效途径之一。阵列误差主要由通道不一致性、天线互耦以及阵元位置不精确等原因引起［7］，因此可以统一表现为阵列的幅度误差、相位误差以及位置误差。

1 均匀圆阵Capon算法

线性约束最小方差准则可表示为:

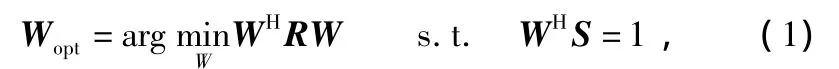
利用拉格朗日乘子算法，此时最优权值为:

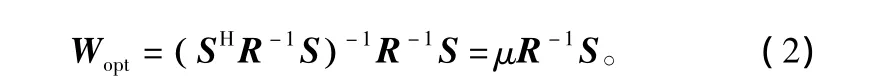
其中，W=［w1，w2，…，wM］T为 M ×1 维向量，M 为阵列天线的阵元数;R为M×M维的接收信号协方差矩阵;S为M×1维的约束向量。当信号方向未知时，有 S=［1，0，…］T。如果信号方向已知，S=［S1，S2，…SM］为其空间方向矢量。图1为均匀圆阵条件下的空间导向矢量模型示意图，在该模型下，空间方向矢量中的元素可表达为如下形式:

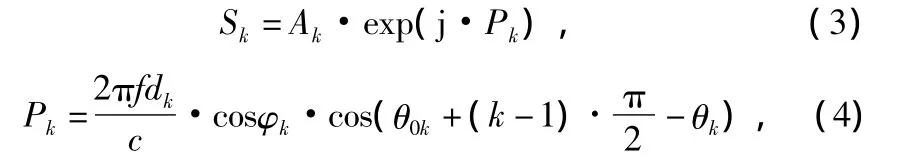
式中，k=1，2，…，M;f为信号中心频率;dk为每个阵元与阵列中心之间的距离;c为光速;φk为等效的信号俯仰角;θk为等效的信号方位角，θ0k为等效的第1个阵元方位角，Ak为标准增益。对于图1所示的模型，如果没有阵元误差，则有 θ0k=π/4，Ak=1，dk=λ/2，λ为信号中心频率的波长。

空间方向矢量S代表着Capon算法的波束指向。当存在阵列误差时，各种阵列误差可归结为空间方向矢量的畸变，从而使波束指向发生偏移，此时Capon算法将无法保证信号方向的增益。

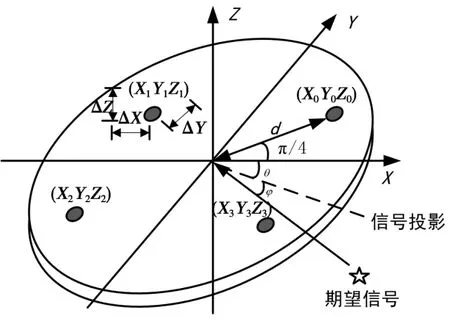
图1 均匀圆阵空间导向矢量模型

2 阵列误差建模

2.1 幅相误差模型

阵列天线存在幅相误差时的模型可等效于在空间导向矢量的幅度和相位上增加一定的扰动，这种扰动在每个阵元上是随机的。例如，当天线存在幅度误差时，此时空间导向矢量中的增益可表达为:

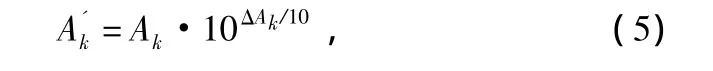
式中，ΔAk为第k个阵元上的幅度偏差，其单位是dB。当阵列天线存在相位误差时，式(4)中的Pk可重新表达为:

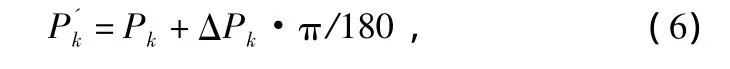
式中，ΔPk为第k个阵元在频率f上的相位偏差，其单位是(°)。因此，存在阵列幅相误差时的圆阵空间方向矢量可以重新表达为:

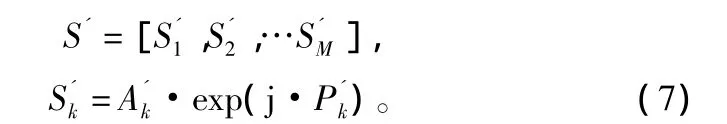
2.2 位置误差模型

当阵列天线存在水平位置误差时，式(4)中的dk和θ0k将发生变化，此时有:

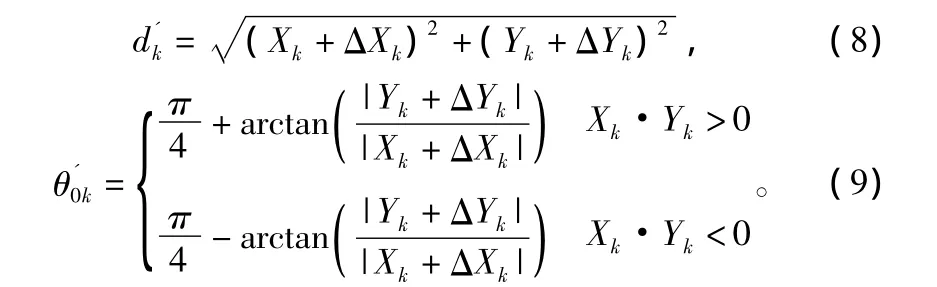
式中，ΔXk、ΔYk分别为水平面内2个相互垂直方向上的位置误差。因此，当天线存在水平位置误差时有:

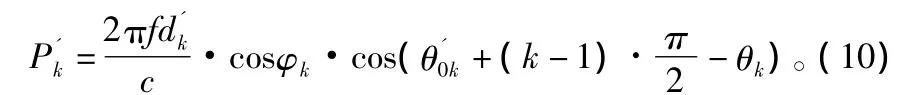
当阵列天线存在法线方向上的垂直位置误差时，式(4)中的dk和φk将发生改变，并有:

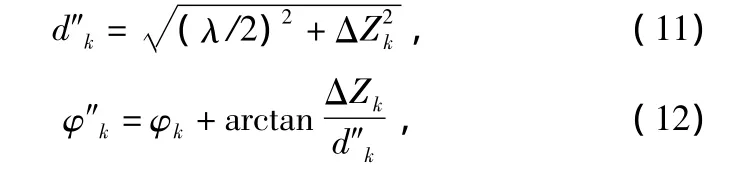
此时，Pk应重新表达为:

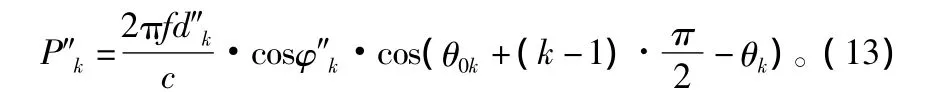
式(3)与式(4)是空间方向矢量的基本模型。如果阵列存在幅相误差，则应采用式(5)、式(6)和式(7)进行建模;如果阵列存在水平位置误差，则可采用式(8)、式(9)和式(10)进行建模;如果阵列存在垂直位置误差，则应采用式(11)、式(12)和式(13)进行建模。下面将给出上述阵列误差模型对Capon波束形成算法影响的仿真结果。

3 仿真结果分析

3.1 仿真条件

假设阵列天线为4阵元均匀圆阵，阵元间距为λ/2，所加载的误差是均值为零、方差可变的正态分布随机值，并且每个阵元的误差单独加载。每种误差对Capon算法性能影响的分析均采取100次蒙特卡罗仿真作为全体样本，并求取其对理想性能改变的方差值作为评估阵列误差对算法性能影响的依据。由于不同方位角上，阵列误差对算法性能的影响是各向同性的，因此这里仅分析不同俯仰角所带来的影响。

3.2 幅相误差仿真结果

图2为不同俯仰角处阵元幅度误差对波束幅度的影响示意图，由其可知，不同俯仰角处的改变规律基本相同，且波束增益改变方差同通道增益方差之间大致呈1:3的线性关系，当通道增益方差为1 dB时，波束增益改变方差仅为0.3 dB左右。因此阵元幅度误差对算法的影响不大。

图3给出了不同俯仰角情况下阵元相位误差对波束指向的影响，由该图可知，相位误差方差在10°以内时，其与波束指向偏差方差之间基本呈线性变化关系。在低俯仰角处，相位误差对波束指向俯仰角的影响较大;在高俯仰角处，相位误差对波束指向方位角的影响较大。而且相位误差方差对俯仰角20°处的俯仰角影响与对俯仰角70°处的方位角影响基本相同，与此相似，相位误差方差对俯仰角70°处的俯仰角影响与对俯仰角20°处的方位角影响基本相同。这说明相位误差对波束指向影响在不同俯仰角处具有一定的对称性，这种对称性是由圆阵空间导向矢量的形式所决定的。

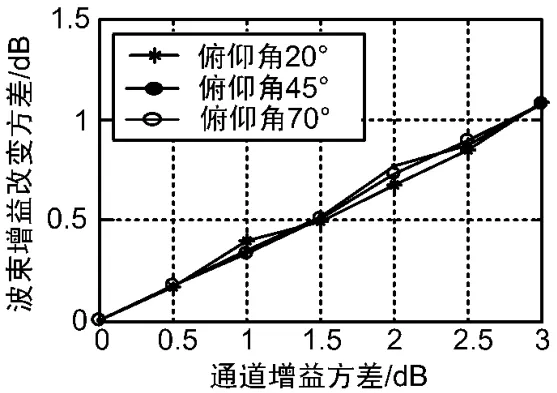
图2 阵元幅度误差对波束幅度的影响

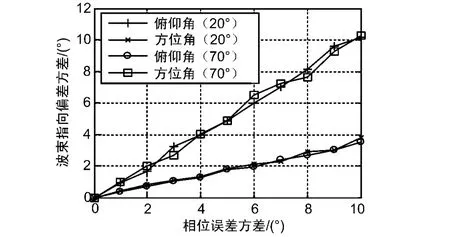
图3 阵元相位误差对波束指向的影响

3.3 位置误差仿真结果

不同俯仰角情况下阵元水平位置误差对波束指向的影响如图4所示，水平位置误差在5 mm以内时，其与波束指向偏差方差之间基本呈线性变化关系。在低俯仰角处，水平位置误差对波束指向俯仰角的影响较大;在高俯仰角处，水平位置误差对波束指向方位角的影响较大。

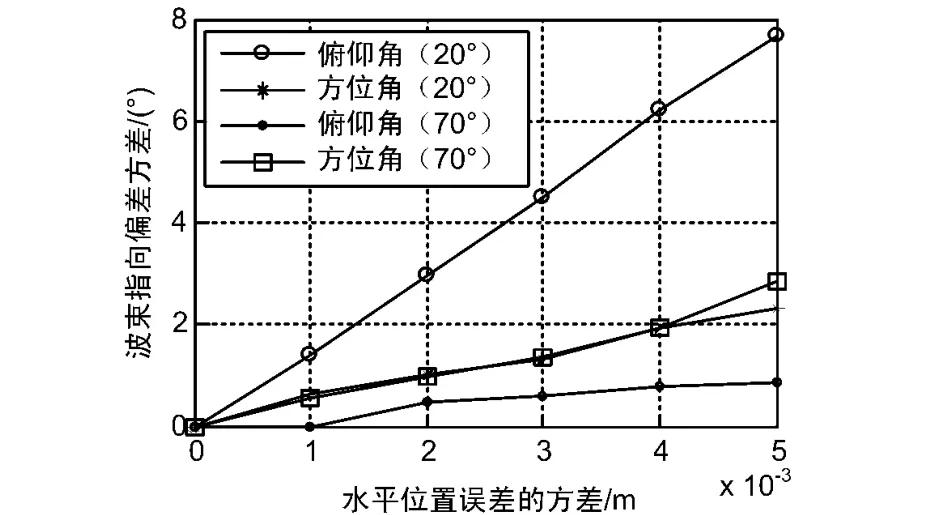
图4 水平位置误差对波束指向的影响

图5则展示了不同俯仰角情况下阵元垂直位置误差对波束指向的影响，由该图可以看出，垂直位置误差在5 mm以内时，其与波束指向偏差方差之间基本呈线性变化关系。在低俯仰角处，垂直位置误差对波束指向俯仰角的影响较大;在高俯仰角处，垂直位置误差对波束指向方位角的影响较大。

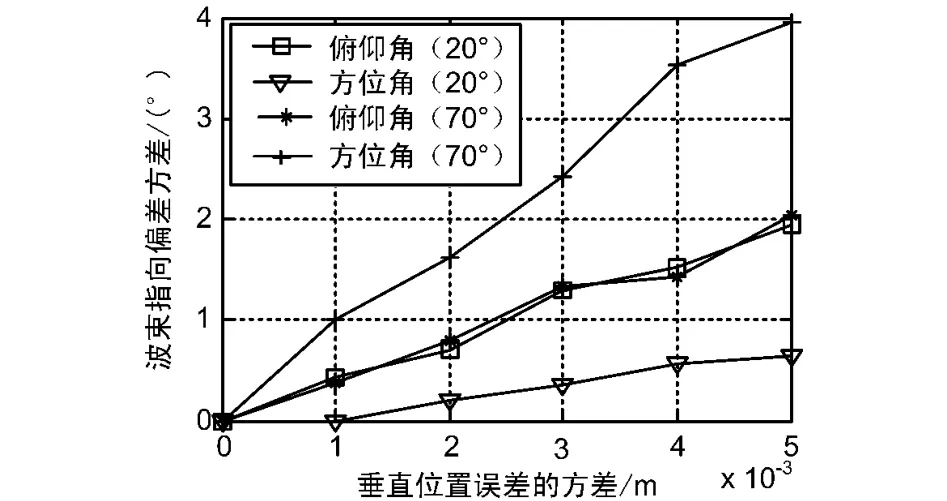
图5 垂直位置误差对波束指向的影响

比较图4和图5还可以发现，存在水平位置误差时，当信号俯仰角变化时，波束指向的方位角偏差对此变化不敏感，在俯仰角20°和俯仰角70°处，2条曲线基本重合，而波束指向的俯仰角偏差对此变化较敏感;当存在垂直位置误差时正好相反，当信号俯仰角变化时，波束指向的俯仰角偏差对此变化不敏感，在俯仰角20°和俯仰角70°处，2条曲线也基本重合，而波束指向的方位角偏差对此变化较敏感。

4 结束语

综上所述，根据上面的建模与仿真结果，可以得到如下结论:对于4阵元的均匀圆阵，阵元幅度不一致性方差与Capon波束增益偏差方差之间基本呈3:1的线性关系，幅度不一致性对算法影响不大;阵元位置误差对波束指向偏差的影响较小，从目前的天线工艺水平来看，该影响可忽略不计;对于4阵元均匀圆阵，阵元相位不一致性方差与Capon波束指向偏差方差之间可呈1:1的线性关系，因此阵元相位误差对Capon算法的性能影响较大。在工程实现时，必须对天线阵元间的相位不一致性作严格的指标约束，或者必须对天线进行标校以减轻该影响。

［1］CAPON J.High Resolution Frequency-wavenumber Spectrum Analysis［J］.Proceedings of IEEE，1969，57:1408-1418.

［2］BUCKLEY K M，GRIFFTHS L J.An Adaptive Generalized Sidelobe Canceller with Derivative Constraints［J］.IEEE Trans on Antennas Propagat，1986，34(3):314-319.

［3］CARLSON B D.Covariance Matrix Estimation Errors and Diagonal Loading in Adaptive Arrays［J］.IEEE Trans on Aerospace andElectronicSystems，1988，24(4):397-401.

［4］GUERCI J R.Theoryand Application ofCovariance Matrix Taper for Robust Adaptive Beamforming［J］.IEEE Trans on Signal Processing，1999，47(4):977-985.

［5］LI Jian，STOICA P，WANG Zhi-song.On Robust Capon Beamforming and Diagonal Loading［J］.IEEE Trans on Signal Processing，2003，51(7):1702-1714.

［6］崔伟，骆鲁秦，李云鹏.导向矢量存在匹配误差时Capon波束校正算法［J］.数据采集与处理，2009，24卷增刊(10):84-87.

［7］王鼎，吴瑛.一种新的阵列误差有源校正算法［J］.电子学报，2010，38(3):517-524.