基于白光干涉原理的光纤传感技术－Ⅱ.光纤白光干涉测量的基本方法

苑立波

（1.哈尔滨工程大学 理学院 光子科学与技术研究中心，哈尔滨 150001；2.黑龙江省光纤传感科学与技术重点实验室，哈尔滨 150001）

0 引言

本文主要讨论的是应变与温度的测量。但是由于任何应变的测量，都无法避免温度变化带来的干扰，所以在实际应用中，通常要在测量应变的同时监测被测结构的温度变化。考虑热膨胀效应和温度对光纤折射率的影响，便可得到纯机械应变。另外，在光纤应变测量中通常假设应变场是完全轴向分布的，亦即，应变仅存在于沿着光纤的方向。

事实上，光纤本身所感知的应变与基体结构的应变相关，但二者不完全一致。本文主要讨论应变从基体到光纤的传导机制，通过监测光纤中传输的光信号的变化来获得外部的应变和温度信息。对传感系统进行标定时，在基体结构上施加一个已知的温度和应变。这个应变场通过某些边界层传输到光纤，具体的传输机理将在以后介绍。光纤因此而产生的相关参数（例如光程差）的变化结果通过干涉解调单元（例如Michelson 或者Mach－Zehnder干涉仪）的机械位移而解调出来。通过标定实验得到的系统参数，可以在使一个未知应变施加于基体结构上的时候，使系统以一个对应的信号作为输出，其数值大小对应于测定的基体结构中的应变。

1 光纤应变与温度传感基本方程

白光光纤传感器的基本参数是传感部分的光程。在均匀条件下，光程可以表示为：

式中n为光纤纤芯的有效折射率；L为光纤传感器的标称长度。

一般地，光程是外加应力σ和温度T的函数，可以表示成为：

光程的变化产生的增量可表示为：

式中dσ和dT分别是局部应变和温度的变化量，［∂S／∂σ］T和［∂S／∂T］σ分别是S对σ和T的导数。

由式（1）中给出的光程，对于σ和T的变化，光程改变可以进一步展开为［1］：

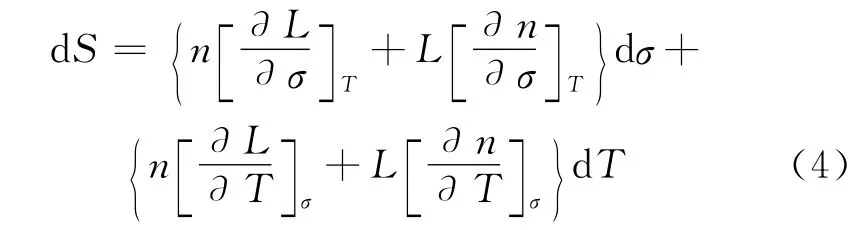
将（4）式稍加改写，得到如下形式：

引入杨氏模量Ef和热膨胀系数αf，则式（5）转化为：

考虑到S＝nL和胡克定律dε＝dσ／Eg，式（6）可以简化为：

这里系数Cε和CT分别定义为：

对于标准的SMF－28型光纤，其应变系数Cε和温度系数CT对于工作在波长为1 300nm 的光源而言，分别为－0.133 2×10－6／μm和0.762×10－5／℃，在1 550nm 处分别为－0.164 9×10－6μm和0.811×10－5／℃［2］。光纤的热膨胀系数为5.5×10－7／℃。

这里，下式是很有用的：

式中dn是由于机械应变dε引起的光纤折射率的改变量。根据光弹效应理论，由于光线性极化出现在i方向的折射率的变化量dni，与应力场εj（j＝1，2，…，6，其中j＝1，2，3分别表示沿z、x和y方向的主应变，j＝4，5，6 分别表示3 个切向应变）的关系可以表示为［3］：

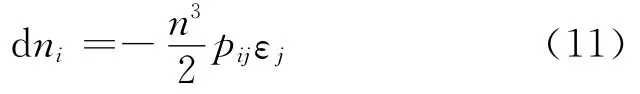
式中pij为光弹系数，用下标1表示沿着光纤的轴向z，2和3分别表示处于光纤横截面内的两个正交方向x和y，见图1。

图1 光纤应变计的归一化长度变化与应变、光弹系数和相对折射率的关系示意图Fig.1 Schematic of the normalized change in the sensor gauge length as a function of strain，the photo－elastic coefficients，and the relevant index of refraction for a fiber optic sensor

因此，光纤传感器测量的温度和应变变化对在光纤中传输光特性的影响，可以由下列基本关系给出：

上述等式用于描述光纤归一化的传感器光程变化量。在一般情况下，沿光纤轴向的参考应变εz0可以取为零，且不考虑温度变化即dT＝0，因此，在恒温的条件下得到：

在均匀各向同性介质中，光弹张量只依赖于两个独立的参数（即光弹系数p11和p12），可以表示如下：

若假设应变场是纯粹轴向应变，亦即，只存在于沿着光纤的方向，可以给出：

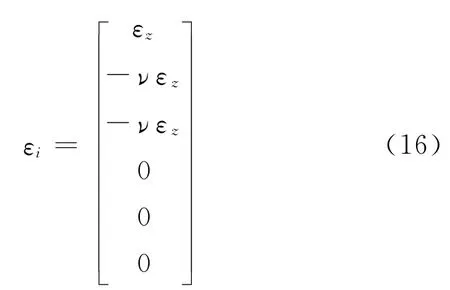
式中ν为光纤的泊松比。这种简化源于Butter和Hocker的早期论文［4］，后来的研究者在光纤应变测量中继续沿用这个简化的表达式。然而在实际应用中，这个假设只适用于表面粘贴或者埋入内部的传感器，在具有轴对称性的平面载荷情况［5］。

根据Butter和Hocker的假设，将式（14）和式（16）代入式（13），在恒温、光纤均匀各向同性且仅存在轴向应变的条件下，可以得到光纤应变与光程的关系：

对于更为一般的应变场（定义3 个主应变｛εz，εx，εy｝）的情况，将假设εz为光纤轴向的应变，对于光矢量中的电场E分量分别在x和y方向，其归一化光程变化量可分别表示为：

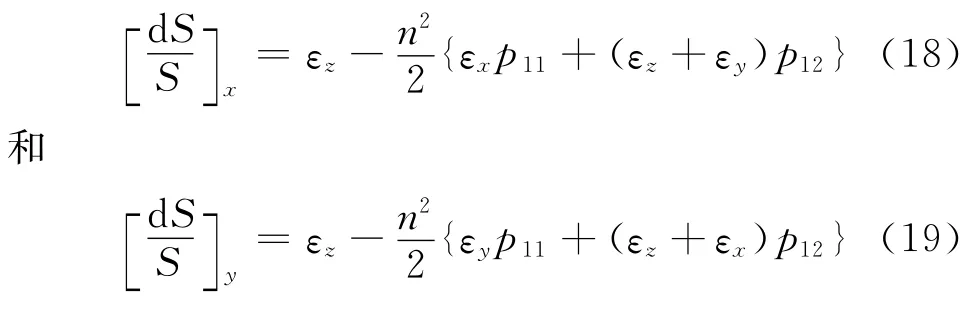
2 光纤白光干涉仪工作原理

自从1880 年发明干涉仪之后，Michelson 干涉仪一直被用来测量微小的空间位移。常用的实验室测量位移的方法有条纹计数法或白光条纹零光程法［6］。使用单色或者高相干光源干涉仪进行绝对位移测量所存在的主要困难是仅能实现对应为弧度相位范围内光程差的测量，超过此范围，将对应一个周期性的输出信号。为了解决这个问题，人们提出了光纤白光Michelson干涉仪［7］并用于温度和绝对位移的测量［8－9］。在白光干涉仪中，可以精确地确定干涉条纹信号中主干涉中央条纹的位置［10］。

光纤Michelson干涉仪的结构见图2。该干涉仪中，作为参考臂和测量的两臂通过使用一个3 dB的耦合器对光进行了分路和合路，同时利用一个扫描镜来改变干涉仪两臂的光程差（OPD）。当干涉仪两臂之间的光程差小于光源的相干长度时，就会产生一个白光干涉图样。干涉图样的中央条纹位于干涉条纹的中心且具有振幅极大值，它对应于干涉仪两臂的光程绝对相等。部分相干传输函数可以用描述光源光谱特性的自相关函数进行表示。

图2 光纤白光Michelson干涉仪Fig.2 Fiber optic white－light Michelson interferometer.

对于LED 光源，光谱的强度分布可以用一个高斯函数［11］来描述，见图3。

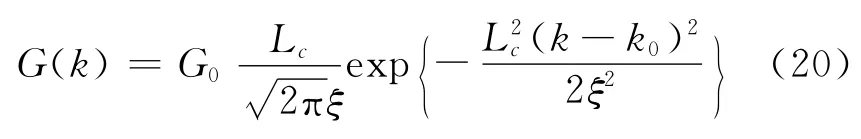
式中Δλ为光源半谱宽度（FWHM），见图3。表1给示出了典型的1 300nm 波长LED 光源的各参数值。

图3 低相干光源的高斯光谱分布Fig.3 Gaussian specral intensity profile from a typical low coherence light source（e.g.LED）

表1 LED 光源的相关参数Table 1 Relative parameter of LED light source

考虑谱密度为G（k）的单色光分量，这里k为波数，光纤Michelson干涉仪的输出光强与光程差x的函数可以写成：

式中α是2×2光纤耦合器的插入损耗系数，定义为α＝（输出总光强）／（输入总光强）；R1是传感臂光纤端面的反射率；R2是补偿臂反射镜的反射率；G1（k）和G2（k）分别是耦合传感臂和补偿臂的耦合强度。

对于3dB光纤耦合器，有：

假设R1＝R2＝R，则式（22）变为：

将式（20）代入式（24）中，并且在（－∞～＋∞）区间对整个光谱积分，可以得到：

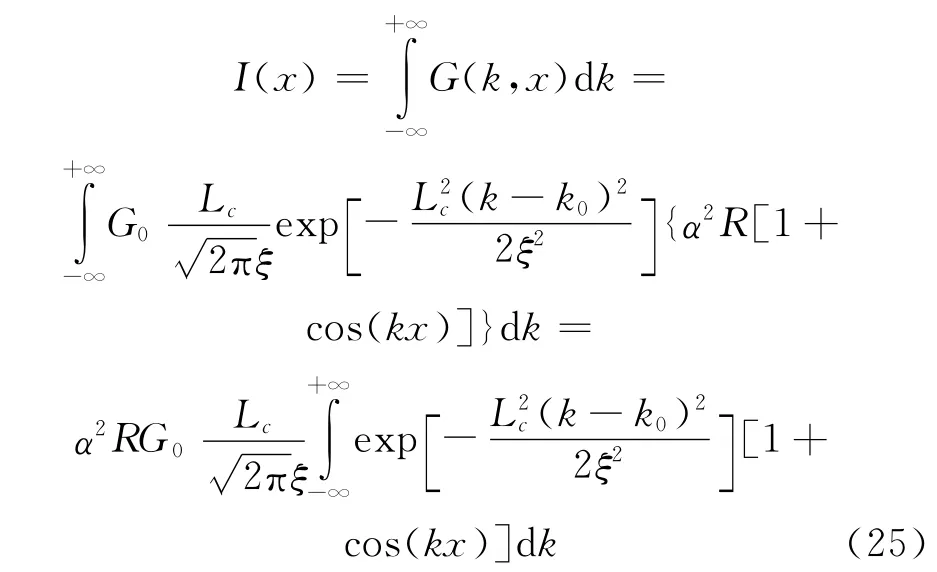
令k＝k－k0，整理式（25），变为：

将表1中的数据代入式（26），并取耦合器的插入损耗α＝0.95和反射率R＝91%，计算得到的归一化白光干涉图见图4。

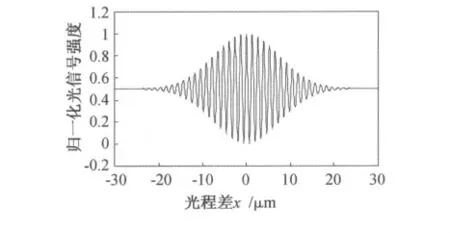
图4 中心波长为1 310nm 的LED光源光纤白光干涉仪的干涉图Fig.4 Output of a fiber optic white light interferometer illuminated by an LED source with a central wavelength 1 310nm

光纤白光干涉技术作为一种有效的方法可以对应变和温度导致的光程变化进行测量。考虑图2中所示的系统，构成传感臂光纤的光程长度是S＝2nL1；参考臂由长度略短于传感光纤的参考光纤L2和参考光纤端面与扫描镜形成的空气间隙X组成。因此参考臂的总光程为2nL2＋2X。

通过调节扫描镜的位置，可以使传感臂和参考臂的光程相匹配，即：

在该位置附近，出现与图4类似的白光干涉图纹。其中，零级条纹近似在干涉条纹图样的中央，具有最大的振幅，对应于两臂光程完全相等处。当传感臂的光程因应变或者周围环境温度改变的作用下发生变化时，这一光程变化量ΔS＝Δ（nL1）可以通过测量反射镜位置的改变量ΔX获得。而反射镜位置的改变量ΔX对应的是零级中央条纹位置的改变量，见图5。

图5 光纤传感器长度变化对应的白光干涉图位置的移动Fig.5 Illustration of fringe pattern shift corresponding to the fiber optic sensor gauge length elongation

扫描镜位移对应传感器光程长度的变化，即：

传感臂连续形变可以通过反复连续测量并记录的方法实现自动测量。因此，可通过这种简单、直接的测量方法实现对应变或者温度的跟踪监测。

3 应变和温度测量技术

在实际应用中，光纤白光Michelson 干涉仪的结构与图2所示的结构相比略有不同，见图6。在传感器的前后两个端面上，各自产生一个传感信号，其中一个信号来自于传感器前端面的部分反射光；而通过该端面的透射光经过长度为L0的传感器，在传感器的后端面发生反射，形成第二个传感信号。当参考臂的反射器进行扫描时，会得到两组干涉条纹。前后两次获得干涉条纹时反射镜的位置差（X＝X2－X1）对应两组干涉条纹的中央条纹：

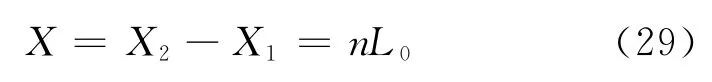
当有负载作用于传感器时，白光干涉中心条纹的位置将发生移动。式（29）变为：

这里，“′”表示载荷施加后的值。

定义：

利用式（29）和式（30），可以得到：

式中ΔL0和Δn表示由被测量（例如：温度T或者应变ε）导致的光纤传感器长度和折射率的变化。

图6 基于白光Michelson干涉仪的光纤传感测量系统Fig.6 White－light Michelson interferometer based fiber optic sensing system

3.1 应变测量原理

当只在传感上施加轴向应变εz时，ΔL0可以表示为：

折射率的变化可以表示为［4］（参见式（11））：

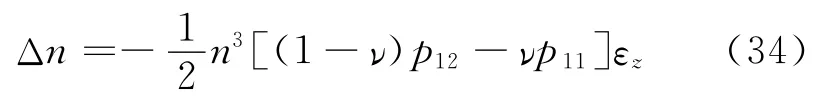
将式（33），式（34）代入式（32）：

3.2 温度测量原理

当环境温度从T0变化到T时，式（32）中的ΔL0和Δn可表示为：

将n＝n（λ，T0），L0＝L0（T0）以及式（37）和式（38）代入式（32），得到：

重写式（40），得到：

表示传感长度为L0的白光干涉光纤传感器的灵敏度，ℑ是灵敏度系数。对于标准单模通信光纤，根据文献［12］，在波长λ＝1 310nm 处n0＝1.468 1，αT＝5.5×10－7／℃，CT＝0.762×10－5／℃；在λ＝1 550nm 处n0＝1.467 5，αT＝5.5×10－7／℃，CT＝0.811×10－5／℃。利用这些数据，可以得到单位长度的光纤在1 310nm和1 550nm处，其温度传感器的灵敏度系数ℑ分别为11.99（μm／m·℃）和12.71（μm／m·℃）。

4 热表观应变与温度补偿技术

热表观应变对于应变测量来讲是一个共性的问题，传统的应变片必须进行温度补偿，以克服测量过程中温度的波动。因此，对于光纤应变测量系统，同样需要温度补偿技术。

为了更好地理解热表观应变，考察光纤被粘贴在参考温度为T0的基体结构上的情况。如果该结构对于外部机械载荷是自由的，当经历了一个小的温度波动ΔT，由于光纤与结构基体材料的热膨胀系数的不一致，在光纤中会产生了一个附加应变。这个热致轴向应变可以表示为：

式中Eg为光纤的杨氏模量；αm和αg分别是光纤与基体材料的热膨胀系数。将应力增量表达式（43）代入式（7），可以得到：

由式（44）可见，即使光纤与基体材料的热膨胀系数一致（即αm＝αg），由于温度系数CT的数量级比基体材料热膨胀系数αm大，因此存在平均温度表观应变的问题。

常用的一种处理表观应变的方法是在应变的测试中独立进行温度的测量，然后对所测的的应变加以修正。当应力诱导产生应变时，对于光纤传感器，可得到更加完整的表达式：

上式可以写成更紧凑的形式：

式中：

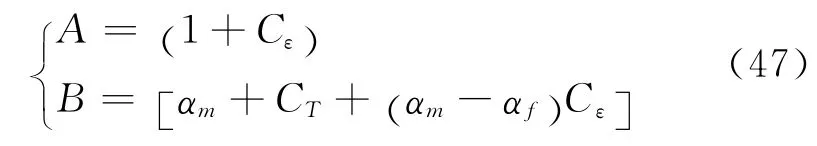
如果设计并安装一个只对温度响应的传统传感器或光纤传感器，对温度进行独立测量，那么式（46）中温度改变项变就是已知的，只有应变是未知的。

另外一种方案是用两种方法进行同时测量，每个测量结果都与温度和应变有关。可以通过这两项测量来确定未知的应变和温度。通常，可以用矩阵的形式来表示：

将矩阵转置，可以得到Δε和ΔT：

因此，可以求得应变和温度：

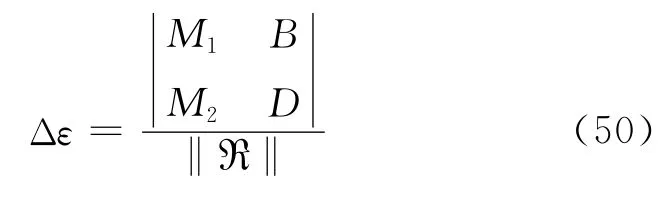
这里，行列式：

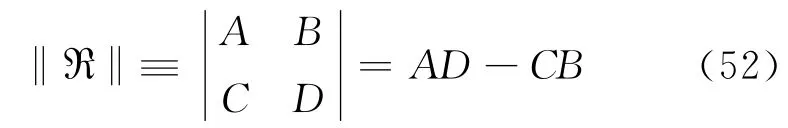
必须为非零值。事实上，对于两次独立的测量，温度和应变系数的差异越大，这种转置运算越精确。如果式（51）中ℜ行列式是病态矩阵，那么两次独立测量中的微小误差δM1和δM2，在求解式（53）和式（54）时也会转变为一个很大误差。同样，注意到应变误差δε和温度误差δT，与光程变化测量误差之间的关系是一致的。可以通过式（52），对于δM1和δM2这一对等式进行变换得到［14］：

上式清楚地显示，需要确保不同系数测量具有较大差异才能确保式（52）非病态，对于差异较小的情况，在测量中会出现较大的误差。

对于白光干涉光纤传感器，可采用两个独立的传感器对温度和应变进行测量，一个传感器埋入基体材料内部，另一个传感器只用于对应变传感器附近的温度测量，于是有：

因此，可得到应变和温度的变化量：

上述讨论的一个重要假设是在载荷应变或者温度变化中应变系数和温度系数恒定且不相关。对于引入的非线性交叉项的情况，这个假设是无效的，并且会给解读传感器输出的信号带来更大的困难。非线性的出现，是由于在式（43）的原始泰勒展开式中，只考虑了线性因子。对于Δε和ΔT数值较大的情况，需要考虑展开式中的高阶项，高阶项是应变和温度的交叉敏感项，由此产生的应变和温度交叉系数Cε，T和Δε与ΔT的变化量为：

式中交叉系数的值为Cε，T～10－8rad0C－1με－1m－1［15］。

上述结果表明，对于自由光纤，除了在较大的应变和温度漂移的情况下，其它情况下该交叉项可以忽略［13，15］。但是，同样可以看到，交叉系数与光纤的长度成正比，长的光纤传感器比短的传感器更容易受应变和温度变化的影响。

［1］Measures，R.M.Smart composite structures with embedded sensors［J］.J.Composites Eng.，1992，2：597－618.

［2］Yuan，L.B.Effect of temperature and strain on fiber optic refractive index［J］.Acta Optica Sinca，1997，17：1 713－1 717.

［3］Nye，S.F.Physical properties of crystals［M］.Oxford Press，London，1954：235－259.

［4］Butter，C.D.，Hocker，G.P.Fiber optic strain gauge［J］.Applied Optics，1978，17：2 867－2 869.

［5］Sirkis，J.S.A unified approach to phase－strain－temperature models for smart structure interferometric optical fiber sensors：Part I-development［J］.Opt.Engineering，1993，32：752－763.

［6］Born，M.，Worlf，E.PRINCIPLES OF OPTICS，4th ed.，［M］.Pergamon Pr.，Oxford，1970.

［7］Beheim，G.Fiber－optic thermometer using semiconductor etalon［J］.Electron.Lett.，1986，22：238－239.

［8］Gerges，A.S.，Farahi，F.，Newson，T.P.，et al.Fiber－optic interferometric sensor utilizing low coherence length source－resolution enhancement［J］.Electron.Lett.，1988，24：472－474.

［9］Li，T.，Wang，A.，Murphy，K.，et al.White－light scanning fiber Michelson interferometer for absolute position－distance measurement［J］.Opt.Lett.，1995，20：785－787.

［10］Gerges，A.S.，Newson，T.P.，Jackson，D.A.Coherence tuned fiber optic sensing system，with selfinitialization，Based on multimode laser diode［J］.Appl.Opt.，1990，29：4 473－4 480.

［11］Yuan，L.B.White light interferometric fiber－optic strain sensor with three－peak－wavelength broadband LED source［J］.Appl.Opt.，1997，36：6 246－6 250.

［12］Yuan，L.B.Optical path automatic compensation low－coherence interferometric fiber optic temperaturesensor［J］.Optics ＆ Laser Technology，1998，30：33－38.

［13］Vengsarkar，A.M.，Michie，W.C.，Jankovic，L.，et al.Fiber optic sensor for simultaneous measurement of strain and temperature［C］／／SPIE，1367，Fiber Optic and LasersⅧ，1990，249－260.

［14］Michie，W.C.，Culshaw，B.，Thursby，G.，et al.Optical sensors for temperature and strain measurement［C］／／SPIE，2718，1996：134－146.

［15］Farahi，F.，Webb，D.J.，Jones，J.D.C.，et al.Simultaneous measurement of temperature and strain：cross－sensitivity considerations［J］.J.Lightwave Tech.，1990，8：138－142.