基于可变集的建筑结构地震损伤评估原理与方法

2012-03-19陈守煜王定乾

黑龙江大学工程学报 2012年2期

陈守煜，王定乾

（大连理工大学建设工程学部，辽宁大连116024）

0 引言

国内外对建筑结构地震损伤评估进行了大量的研究，经历了从力学结构性能指标到以结构性能参数为基础的多指标评估过程［1］。文献［2］利用推覆分析得到结构损伤指数，并将该指数与能力谱法相结合，建立了单指标结构损伤评估模型，对钢筋混凝土结构三水准抗震设计损伤性能目标做了改进；文献［3］在文献［2］的基础上，又增加了3个抗震损伤指标：最大层间位移角、滞回耗能循环次数和楼层能量集中系数，并采用模糊综合评判方法确定多因素与模糊损伤集合的关系，实现对结构抗震损伤多指标分析和评估。该法将以前的单指标评估标准增加为4个指标，拓展了钢筋混凝土结构三水准抗震设计地震损伤性能目标；文献［4］在文献［3］基础上采用物元分析，建立结构抗震损伤评估模型。但由于物元分析（可拓学）在基础概念上存在数学逻辑等错误［5－6］，因此，物元分析结构抗震损伤评估模型缺乏科学依据。文献［7］应用集对分析评价法［8］提出钢筋混凝土结构地震损伤评估多元联系数模型。但因集对分析评价法存在数学推理错误［9－10］，因而结构地震损伤评估多元联系数模型同样缺乏科学依据。文献［11］根据地震损伤评估的设防水准和损伤程度是亦此亦彼的模糊概念提出基于可变模糊集的建筑结构地震损伤评估原理与方法。本文进一步考虑到建筑结构损伤进行评估所依据的各项指标是非此即彼的清晰值，根据笔者最近提出的可变集理论［12］，将地震损伤评估中“非此即彼”的清晰性指标与 “亦此亦彼”的地震损伤模糊概念进行辩证的综合分析，提出基于可变集的建筑结构地震损伤评估原理与方法。

可变集是从可变模糊集发展而来，两者有着密切的联系，但又有本质上的区别，可变模糊集隶属于模糊系统，可变集属于普适系统，它既包含模糊系统，又包含清晰系统，是可变模糊清晰混合系统。可变集研究事物、现象及其反映（思维与概念）非此即彼清晰性与亦此亦彼模糊性两者辩证的对立统一理论。它既研究事物、现象的量变，更研究其质变，是对康托普通集合论与札德模糊集合论概念的突破，有重要的科学意义与应用价值。

1 可变集的辩证法基本规律数学定理

1.1 可变集的对立统一定理

设U为论域，u为U中的元素，u∈U。u的对立即事物与现象的对立属性，无论是非此即彼的清晰性对立，还是亦此亦彼的模糊性对立，均统一记以对立符号与。在连续统的两个端点赋以1与0、0与1的数。在1、0到0、1的数轴上构成一对数的连续统。对于U中的元素u，都在该连续统的任一点上确定了一对对立测度值（u），称为u对的对立相对隶属度。映射：

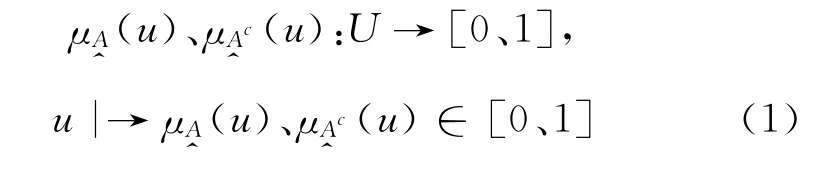
设论域U中元素u的变化，记以C（u），无论对 “非此即彼”还是 “亦此亦彼”的对立事物、现象与概念，变化前有：

在连续统上必存在：

的渐变式质变点。变化后仍有：

式（1）～式（5）组成可变集的基础定理：对立统一定理。

设：

1.2 可变集的质量互变定理

1）如有等式：

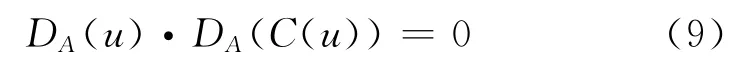
则变化至平衡点即渐变式质变点，系统处于平衡状态。

2）如有不等式：

3）如有等式：

4）如有不等式：

式（9）～式（12）统称为可变集的质量互变定理。

1.3 可变集的否定的否定定理

若变化为N个周期，变化后终了状态在Pr点（N为奇数）或Pl点（N为偶数），即N次否定则有：

当N＝2时，即两次否定，故否定的否定定理可表示为：

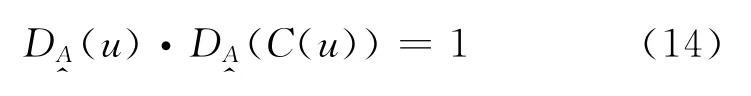
式（14）称为可变集的否定的否定定理。

2 基于可变集的建筑结构地震损伤评估原理与方法

建筑结构损伤与非损伤是亦此亦彼的对立模糊概念，影响该模糊概念的因子或指标，根据文献［3］的研究，其指标体系：整体损伤指数，最大层间位移角，滞回耗能循环次数，楼层能量集中系数都是清晰的确定值。因此建筑结构地震损伤评估是可变模糊清晰混合集即可变集。下面应用可变集的对立统一定理、质量互变定理，提出建筑结构地震损伤评估可变集原理与方法。

根据文献［3］关于建筑结构抗震5级标准：h＝1为基本完好，h＝2为轻微损伤，h＝3为中等损伤，h＝4为严重损伤，h＝5为倒塌。

设评估系统由n个评估对象组成的集合U，u为其中的一个评估对象，u∈U，以指标i的特征值xi对u进行评估。已知的m个指标c个级别的标准值区间矩阵为：

式中aih、bih分别为指标i级别h标准值区间的上、下界；aih可以大于或小于bih。指标i的对立属性A＾与对应于指标i的对立级别h与（h＋1），为了运算方便，符号以替代，以替代。

当h＝1为基本完好级，由物理概念可知，指标i、1级标准值区间［ai1，bi1］的上界ai1对1级的相对隶属度为1，根据对立统一定理，对对立级2级的相对隶属度为0，对应的相对差异度Di1（u）＝1。下界bi1对1级的相对隶属度为0.5，根据质量互变定理，对对立级2级的相对隶属度为0.5，bi1为1级与2级的渐变式质变点。设ki1为对象u在区间［ai1，bi1］内对1级相对隶属度为1的点值，故ki1＝ai1。

当h＝c＝5为倒塌级，根据物理概念，区间［aic，bic］的下界bic对c级的相对隶属度为1，对对立级（c－1）的相对隶属度为0，对应的相对差异度Dic（u）＝1；上界aic对c级的相对隶属度为0.5，对对立级（c－1）的相对隶属度为0.5，即aic为（c－1）级与c级的渐变式质变点。设kic为对象u在区间［aic，bic］内对c级相对隶属度为1的点值，故kic＝bic。

利用多个教学软件开展实训教学，进一步强化任务驱动教学法的开展，与其他课程互相结合，突出课程重点，呼应其他国际贸易环节。具体可以遵循以下过程，首先使用外贸流程模拟实训平台中的DOC系统对国际结算票据和信用证开证申请书进行填制练习，在此基础上使用国际结算专业实训软件对结算方式的流程进行操作，这样既强化了学生对主要票据和结算方式的掌握，又节省了课内时间，可以在有限的实训学时内，安排更多的练习，让学生完成较多的课程任务。

对1级ki1＝ai1，对c级kic＝bic，对中介级l，满足以上3个条件的kih点值通用模型为：

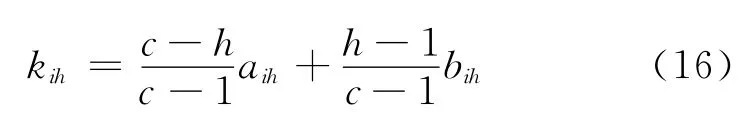
应用式（16）可得到评估对象u相对差异度Dih（u）＝1的点值矩阵：

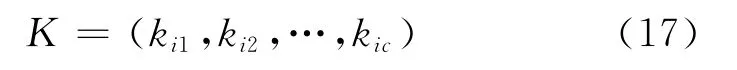
设评估对象u的特征值xi落入矩阵（17）中相邻两级（h与h＋1级）区间［kih，ki（h＋1）］内，h＝1，2，…，（c－1）。由于区间［kih，ki（h＋1）］对应［Dih（u），Di（h＋1）（u）］＝［1，1］，且存在Dih（u）＝0的渐变式质变点bih，则u的特征值xi对级别h，h＋1的相对差异度可根据模型（18）或（19）计算：

为了运算方便，把相对差异度模型（18）、（19）转变为相对隶属度模型，根据式（2）、式（6）得到相对隶属度与相对差异度的关系：

将式（18）及式（19）代入式（20）得：

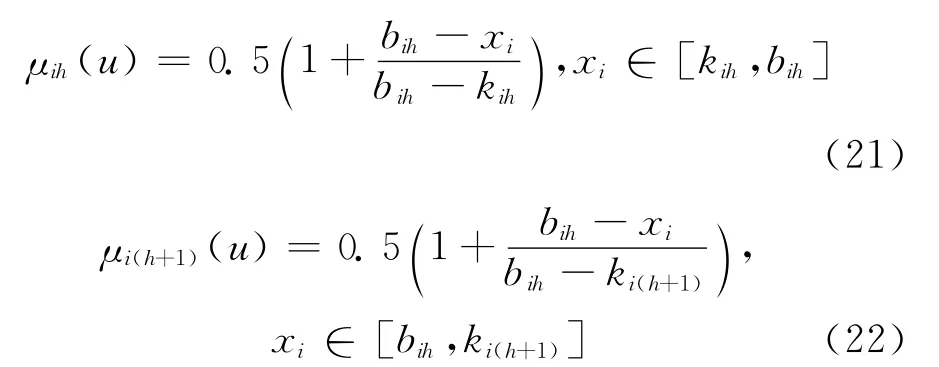
根据物理分析，可知：

式（21）、式（22）是单指标模型，而建筑结构地震损伤评估是多指标综合评估问题，参照文献［6］，评估对象u对级别h的综合相对隶属度模型为：

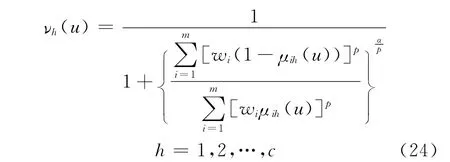
式（24）满足对立统一定理。式中α为优化准则参数，α＝1相当于最小一乘方准则，α＝2为最小二乘方准则；p为距离参数，p＝1为海明距离，p＝2为欧氏距离。根据式（24）可得向量ν→—h（u）。应用文献［13］中的级别特征值公式：

3 应用实例与比较分析

为了比较，引用文献［4］的4座结构地震损伤实例。4座结构分别为：5层均匀框架、15层均匀框架、9层偏心框架和4层不完全对称框架，结构性能指标计算特征值，根据文献［4］如表1所示。表2列出结构三水准抗震设计的地震损伤性能指标标准值区间。

表1 算例结构的性能指标Table 1 Results of performance indexes of example structure

表2 钢筋混凝土结构三水准抗震设计的地震损伤性能指标标准值区间Table 2 Structural seismic damage performance objectives for the three－level earthquake－resistant design

以结构1为例说明，由表2可知结构损伤评估的指标标准值区间矩阵为：

由式（16）和矩阵Y得矩阵K为：

根据表1钢混结构1，4项指标特征值向量为：

由式（21）或式（22）、式（23）与对立统一定理得结构1的4项指标对各级的相对隶属度矩阵为：

为了比较，采用文献［4］同样的指标权向量w＝［0.4，0.2，0.25，0.15］，应用式（24），当参数α＝1，p＝1得结构1对级别h的综合相对隶属度向量为：

级别特征值H（u1）＝3.97，因此结构1为严重损伤。

进行类似的计算，得到4座结构地震损伤评估结果列于表3。表3中同时列出物元分析（可拓学）与集对分析联系数的评估结果。

表3 四座结构损伤评估结果Table 3 Results of structural damage evaluation

4 比较与分析

由表3可见本文与可拓学、集对分析联系数的评估结果有相同也有不同。下面根据笔者在文献［10］中提出的观点：“系统评价不仅要求评价结果符合实际，而且更要求评价理论（或原理）、模型与方法的科学性。”进行分析论述。

4.1 可拓学的基础：可拓集合定义存在数学逻辑错误，可拓学评估结果缺乏科学依据

文献［14］关于可拓集合的定义表述为 “可拓集合则用取自（－∞，∞）的实数来表示事物具有某种性质的程度，正数表示具有该性质的程度，负数表示不具有该性质的程度，零则表示既有该性质又不具有该性质，如一只脚在门内，一只脚在门外的人属于 ‘门内的人’的集合的程度为零”。

可拓集合的定义，得到 “一只脚在门内，一只脚在门外的人属于 ‘门内的人’的集合的程度为零”的结论，是可拓学的数学与逻辑错误的代表。现论述如下：

设某人（u）以体质量w为特征量，u从 “门内人”集合，即对 “门内人”的相对隶属度转化为“门外人”集合的过程中，当u跨向门槛，w／2在门内，另w／2在门外（近似地认为，一只脚在门内，一只脚在门外），此时u具有门内人、门外人的相对隶属度各为（w／2）／w＝0.5或即处于动态平衡状态。根据可变集对立统一定理，有显然此种状态根本不是可拓集合定义所谓的 “属于 ‘门内的人’的集合的程度为零”（即关联函数K （u）＝0）。根据可变集对立统一与质量互变定理应该是显见，可拓学的可拓集合关联函数等于0或K（u）＝0有误。“门内人”、“门外人”属于对称概念，可拓集合认为u属于 “门内人”集合的程度为零，也就是认为u属于“门外人”集合的程度为零。因此， “一只脚在门内，一只脚在门外的人”在可拓集合关联函数K （u）＝0或可拓集合零界概念的定义下，出现了这个 “客观存在”的人 “消失”了的逻辑错误。

可拓集合给出形式化模型：关联函数K （u）＞0、K（u）＝0、K（u）＜0作为事物具有性质P、既具有又不具有性质P、不具有性质P的数学判断准则，并由此给出可拓集合的数学定义，显然，可拓学不是从事物u变化的内因（即内部矛盾）与出发去研究矛盾的相互转化，从而违反了事物矛盾运动变化过程中对立统一及其相互转化的内在联系，根据文中对立统一与质量互变定理，可见可拓学的数学基础可拓集合有违自然辩证法对立统一与质量互变规律。从而出现了“一只脚在门内，一只脚在门外的人属于 ‘门内的人’的集合的程度为零”的基础性错误。

4.2 与集对分析多元联系数评估成果的比较与分析

文献［7］在地震损伤评估中应用的集对分析多元联系数公式（文献［7］的公式（3））来源于《中国科学》杂志2009年第9期发表的文章《水资源系统评价新方法—集对评价法》。笔者已在文献［9］、文献［10］中证明了该法在数学逻辑推理上有误。尽管文献［8］在该法的前面加上 “模糊”两字，即所谓模糊集对评价法，并在文献［8］中多处将该法错误地应用于水文水资源系统评价。但由于集对评价法在基本原理上有误，增加模糊两字并不能改变其错误的性质，因此，文献［7］应用集对分析评价法得到建筑结构地震损伤评估的成果缺乏科学依据。此外，集对分析［15］还存在一些其他的问题与错误（可详见文献［16］），本文不再另述。

5 结语

2008年我国汶川、2009年海地、2010年智利相继发生破坏性大地震，建筑结构的抗倒塌研究引起了人们的高度关注［17］。建筑结构在地震作用下抗倒塌能力是建筑结构抗震设计的最重要的性能目标。我国、美国、日本等多地震国家投入了大量的人力、物力以及科学试验力量，进行了建筑结构在地震作用下的倒塌机理与评估研究。但无论是倒塌机理还是评估研究，严格要求理论上的正确性与科学性。因为在结构抗震研究中预估建筑结构的破坏状态是关系到人民生命财产安全的大事，建立在错误理论基础上的建筑结构损伤评估会带来负面影响。笔者在文献［5］中曾指出： “数学与逻辑错误，在可拓学及其工程领域中不胜枚举，给科学、技术与工程领域造成负面影响。指出可拓学的这些错误，可以有利于尽快消除（尤其在工程领域）由错误所产生的负面影响”。本文指出可拓学与集对评价法的错误，其目的在于尽可能地消除错误所带来的负面影响。

可变集的科学意义在于：可变集架起了一座数学思维辩证化与哲学规律数学化之间联系的桥梁，为实现马克思的名言 “一种科学只有在成功的运用数学时，才算达到了真正完善的地步。”迈出了坚实的一步。可变集突破了模糊系统框架，把建立在可变模糊集基础上的辩证法基本规律数学定理，发展为普适系统的对立统一、质量互变与否定的否定定理（本文第一节中论述的定理）。本文将该定理用于识别可拓学关于一只脚在门内，一只脚在门外隶属于门内人的程度等于零的可拓集合的基础性错误，具有现实意义。

本文提出的建筑结构地震损伤评估原理与方法，可推广应用于普适系统（含模糊系统）等多指标（或多目标）评估或评价领域，诸如水文水资源、水利水电工程、土木工程、环境工程、管理工程等系统，具有宽广的应用前景。

［1］王振宇，刘晶波.建筑结构地震损伤评估的研究进展［J］.世界地震工程，2001，17（3）：43－48.

［2］李宏男，何浩祥.利用能力谱法对结构地震损伤评估简化方法［J］.大连理工大学学报，2004，44（2）：267－270.

［3］何浩祥，闫维明，周锡元.基于性能的钢混框架结构多元模糊地震损伤评估［J］.工程抗震与加固改造，2006，28（1）：100－105.

［4］何浩祥，闫维明，乔亚玲.物元分析理论在钢筋混凝土结构地震损伤评估中的应用［J］.北京工业大学学报，2006，32（9）：791－797.

［5］陈守煜.可变模糊集合理论—兼论可拓学的数学与逻辑错误［J］.大连理工大学学报，2007，47（4）：618－624.

［6］陈守煜.基于可变模糊集的辩证法三大规律数学定理及其应用［J］.大连理工大学学报，2010，50（5）：838－844.

［7］钟延营，杨娜，张勇.钢混结构地震损伤评价多元联系数模型［J］.低温建筑技术，2010，（3）：32－35.

［8］王文圣，李跃清，金菊良，等.水文水资源集对分析［M］.北京：科学出版社，2010.

［9］陈守煜，王子茹.基于对立统一与质量互变定理的水资源系统可变模糊评价新方法［J］.水利学报，2011，42（3）：253－261.

［10］陈守煜.基于辩证法三大规律数学定理的系统评价理论、模型与方法——兼论集对分析及其评价方法［J］.黑龙江大学工程学报，2010，1（1）：11－16.

［11］陈守煜，牛云格，王子茹.基于可变模糊集的钢混结构地震损伤评估原理与方法［J］.水利与建筑工程学报，2011，2（4）：1－6.