高空核爆炸碎片云运动数值模拟

杨 斌 牛胜利 罗旭东 黄流兴

（西北核技术研究所 西安 710024）

碎片云是核爆炸后弹体材料、裂变产物及周围大气在高温、高压下形成的带电粒子云。高空爆炸场景下，带点粒子以极高的初速度向外扩展，对近区空间飞行器有一定的力学破坏；对核爆炸后产生的剩余核辐射、大气电离、人造辐射带、极光及共轭区效应等地球物理现象，也有重要贡献[1]。模拟核爆引起的人造辐射带，须知道带电粒子在地磁场中的初始分布，才能根据扩散损失理论得到人造辐射带的演变规律[2]。因此，研究高空核爆炸初期碎片云的运动行为有重要意义。

采用基于流体力学的滚雪球模型对爆高在 100 km以下碎片云扩展和卷入大气的过程已有报道[3]，但爆高在100 km以上碎片云运动规律的研究较少，特别是250 km以上，由于地磁场的显著作用以及碎片云本身带电粒子运动产生的复杂电磁现象，滚雪球模型不复适用。本文根据碎片云与大气相互作用的特点，考虑地磁场和高空大气带来的影响，通过对连续性方程、动量方程和能量方程做适当修正，构造了描述碎片云运动的磁流体力学方程组，利用拉格朗日差分方法进行求解，研究了典型爆炸场景下爆炸初期碎片云的运动扩展规律。

1 碎片云运动的理论模型

核爆炸初期，由于碎片云处于高温、高压和高速运动的状态，而大气是相对静止的冷气体，两者有复杂的碰撞作用，碰撞电离和电荷交换是重要的碰撞效应。碰撞电离效应是指电中性的大气分子电离成离子，并成为碎片云的一部分；电荷交换作用是指碎片云中部分离子与周围中性分子发生电荷交换，离子成为新的中性分子，而原有的中性分子变为新的离子，成为碎片云的一部分。这些作用使碎片云与周围的稀薄大气分子发生交换，从而改变了自身的状态。本文考虑的高空大气气体为中性大气，未考虑电离状态气体的影响。

根据磁流体力学运动方程一般形式[4]，考虑碎片云运动过程中与大气分子原子的电荷交换、碰撞电离，对一般形式进行修正，得到描述碎片云运动的方程组：

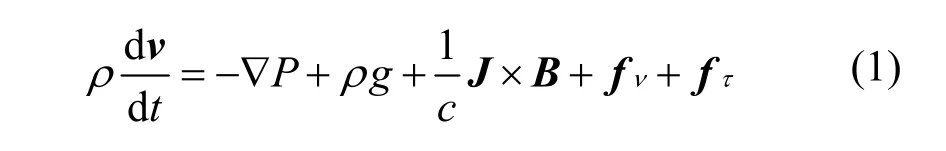
其中，ρ为碎片云的密度；n(σx+σi)为碎片粒子和大气粒子碰撞的阻力项，nn为大气的数密度，mn为大气分子量，mi为碎片云的摩尔质量，σx为有效的电荷交换截面，σi为碰撞电离截面；为碎片粒子的粘滞项，Q是粘滞压强；J为电流强度，包括带电粒子在磁场中运动和磁场变化产生的电流项，即J=j'+j,j'=σν×B,σ为电导率，

利用麦克斯韦应力表达式

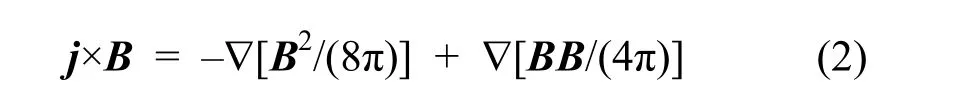
并忽略重力影响，式(1)可表示为

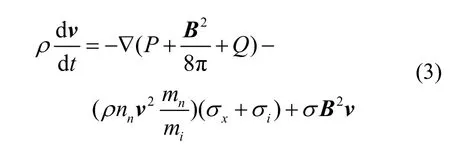
式(3)在一维球坐标下可表示为

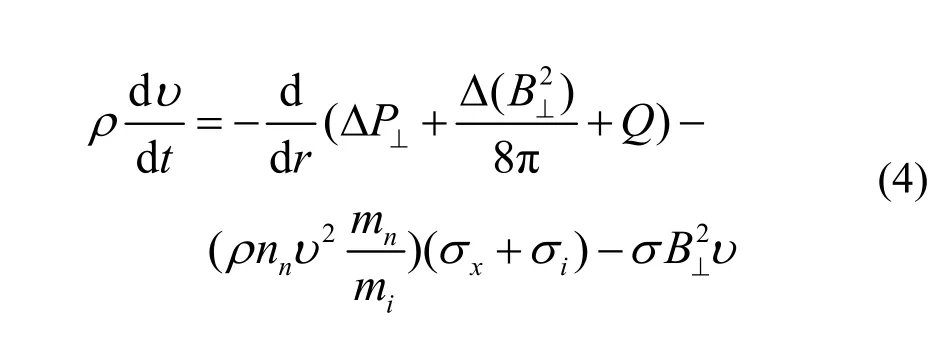
其中表示和径向相垂直的分量，表示垂直磁场的速度引起的压强。

对于无碰撞流体，其微分形式的质量连续性方程为：

若考虑碎片云中离子与环境中性粒子的相互作用，式(5)修正为

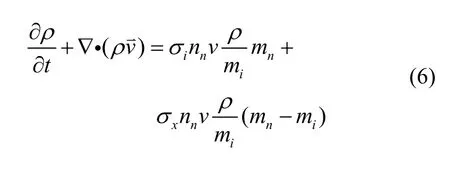
由Maxwell方程组法拉第定律、安培定律、欧姆定律的微分形式：

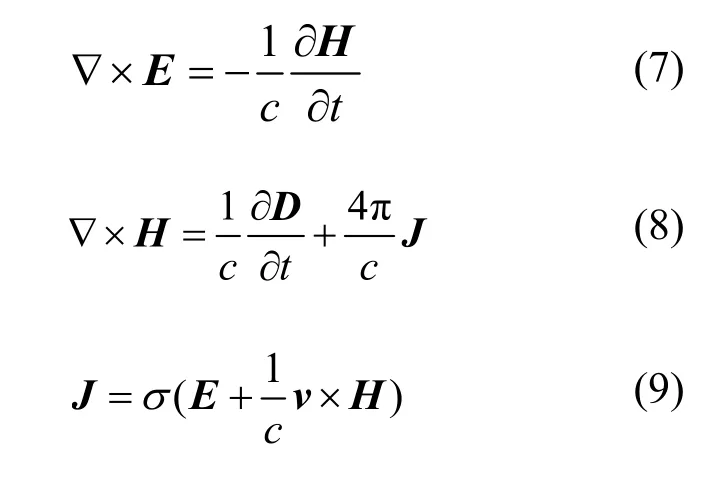
可得到磁扩散方程

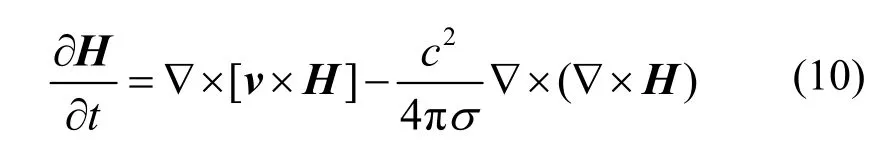
考虑碎片云的磁场是无源场，在球坐标系下垂直于r方向上，式(10)可简化为：

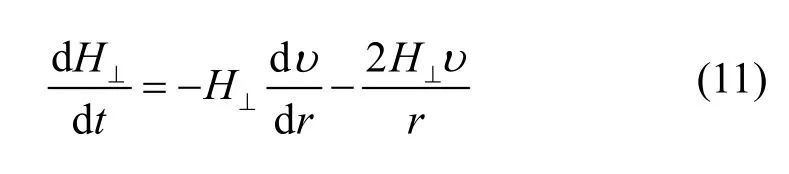
忽略重力势能，对任意的流体，其体内总能量包括了动能和内能，总能量的净增率为：

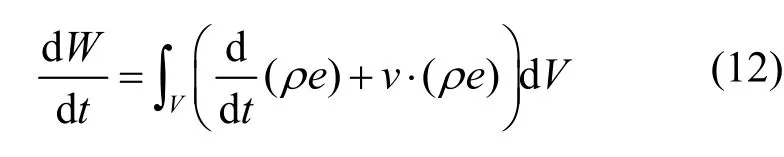
其中，e=ε+ν2/2，ε和ν2/2分别代表内能密度和动能密度。由能量变化和功率的关系：

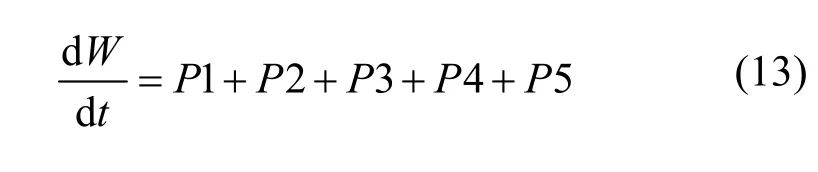
将碎片云迅速膨胀视为绝热过程，并忽略磁流体焦耳热，则外界通过应力张量对碎片云做功的功率为

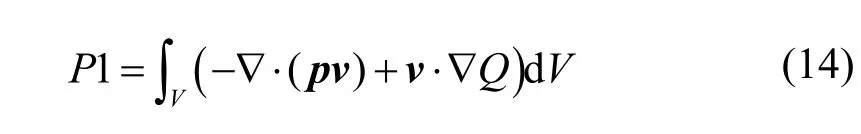
电磁力作功的功率为

因碰撞产生并卷入碎片云的离子对云体能量的增加率，包括离子随碎片云体一起运动的动能和由碰撞导致的随机能量

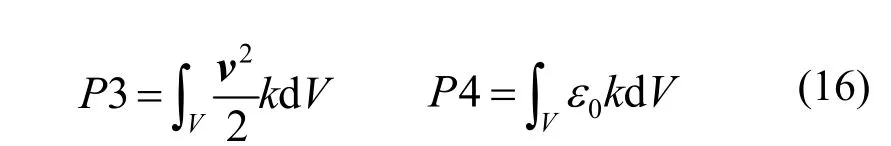
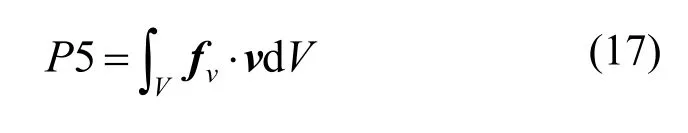
将式(12)、(13)联立，代入各功率分量，可得到

由于物理量P是由B和ν所在平面内的计算决定，故三维问题实际变为二维问题。粒子的自由度为2，地绝热指数相应为γ=2，代入压强关系式

得碎片云压强演变的关系式

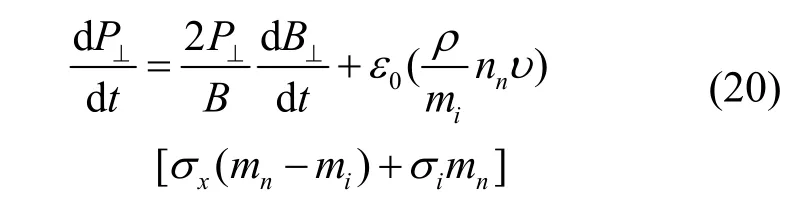
由式(4)、(6)、(11)、(20)联立，得模拟碎片云运动的磁流体力学方程组。

2 数值计算方法

核爆炸使碎片获得巨大动量，并以爆点为中心沿径向高速运动，粒子间在切线方向上的相互作用可略。设碎片云在同一扩散方向上粒子的速度一致，整体的碎片云为壳层结构，忽略壳层区域内部随机扩散效应的少数粒子。碎片云初始时刻的参量由核爆炸的状态方程[5]计算，得初始时刻碎片云的温度、热压强、速度、总压强。

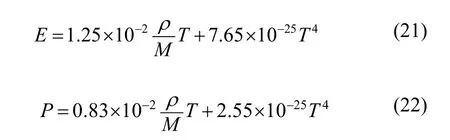
将式(21)、(22)使用拉格朗日格式[6]进行差分：

为提高计算效率，模拟程序实现并行化运算。并行化设计时，由于所用计算模型仅考虑沿爆心径向方向上碎片云的磁流体力学扩展行为，可按空间立体角均匀地分配计算任务给各个CPU。图1为以初始时刻爆点为中心的球坐标系，其中0º≤θ≤180º，0º≤φ≤180º，并行运算时将空间碎片云按θ和φ角划分，图中阴影部分表示为分配任务给某个单CPU的计算范围。

3 计算结果

为验证模拟方法的正确性，本文模拟了 1962年美国的一次典型高空核爆炸试验碎片云的演变，该高空核试验代号为Starfish，爆炸当量为1.5 Mt，爆点在约翰斯顿岛上空400 km。用碎片云环境的程序模拟了碎片云的扩展速度、压强、温度等随时间的演化。

图2的实心数据点为本文模拟计算结果，空心数据点为文献[7]的结果。核爆炸后0.1–0.5 s，碎片云的水平扩展尺度达600 km以上，在垂直方向上，爆点下方距离地面300 km处出现碎片云的沉积，向上距离地面约800 km的高度。本文结果与文献[7]基本吻合。

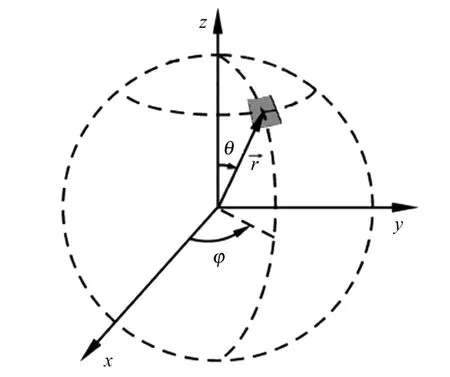
图1 单CPU需要计算的立体角Fig.1 Solid angle of single CPU calculation.

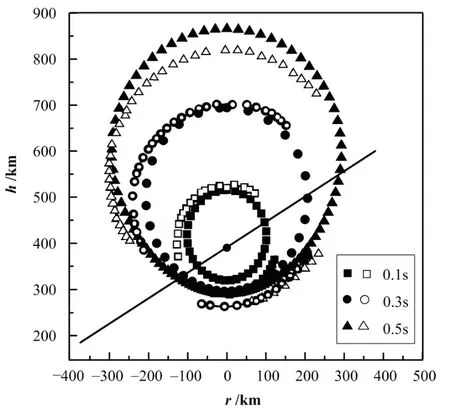
图2 Starfish试验子午面模拟(实心符号)和文献[7] (空心符号)的比较Fig.2 Comparison of the data in the meridian section: the solid symbols, this work; the blank symbols, Ref.[7].

图3给出了Starfish核爆后0.5 s内，碎片云在磁子午面上不同方向扩展速度、压强、温度、数密度随时间的变化。由于高空大气的影响，碎片云0.1 s后在爆点上方速度衰减很慢，而下方大气密度的明显增大，增加了粒子发生碰撞的几率，碎片云的速度迅速衰减。碎片云的压强和数密度的变化趋势类似，爆点上方受到的阻力小，压力释放最快，数密度衰减最快，下方则压力释放最慢，数密度衰减最慢，其它方向居中。碎片云的温度在0.1 s前呈指数下降，而后基本保持和周围大气相近的温度，且各方向差异不大。

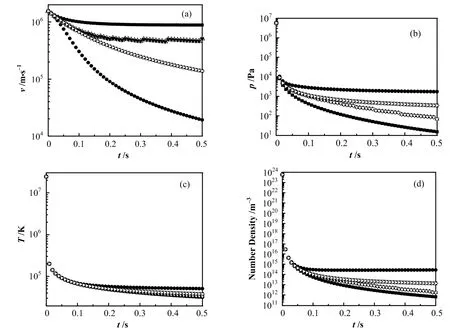
图3 Starfish核爆后0.5 s内碎片云在不同方向上的扩展速度(a)、压强(b)、温度(c)和数密度(d)随时间的变化Fig.3 Expanding speed (a), pressure (b), temperature (c) and number density history of debris in different directions,as function of the time in o.5 s after the Starfish nuclear explosion.

4 结语

高空核爆因为爆点周围环境的特点，爆炸后碎片云的扩展规律明显不同于低空和地面爆炸。本文详细介绍了模拟碎片云运动的磁流体力学理论模型的建立，数值计算方法，并利用该模拟了美国Starfish高空核爆炸试验碎片云的运动参数，部分模拟结果与文献[7]进行了比对，两者基本吻合，证明了碎片云物理模型的正确。

1 王建国, 牛胜利, 张殿辉, 等. 高空核爆炸效应参数手册[M]. 北京: 原子能出版, 2010: 130 WANG Jianguo, NIU Shengli, ZHANG Dianhui,et al.Parameter handbook of high attitude nuclear detonation effects[M]. Beijing: Atomic Energy Press, 2010: 130

2 顾旭东, 赵正予, 倪彬彬, 等. 高空核爆炸形成人工辐射带的数值模拟[J]. 物理学报, 2009, 58(8): 5871–5877 GU Xudong, ZHAO Zhengyun, NI Binbinet al.Numerical simulation of the formation radiation belts by high attitude nuclear detonation [J]. Acta Physica Sinica,2009, 58(8): 5871–5877

3 乔登江, 华鸣. 碎片云的运动[J]. 抗核加固, 1986, 3(2):98–106 QIAO Dengjiang, HUA Ming, Debirs motion [J].Antinuclear Hardening, 1986, 3(2): 98–106

4 吴其芬, 李桦. 磁流体力学[M]. 长沙: 国防科技大学出版社, 2007: 23 WU Qifen, LI Hua. Magnetic hydrodynamic [M].Changsha: National University of Defence Technology Press, 2007: 23

5 乔登江, 韩学安, 李如松, 等. 地下核爆炸现象学概论(上册). 北京: 国防工业出版社, 2002: 43–44 QIAO Dengjiang, HAN Xue’an, LI Rusong,et al,Phenomenological Introduction of Nuclear Detonation.Beijing: National Defence Industrial Press, 2002: 43–44

6 傅竹风, 胡友秋. 空间等离子体数值模拟[M]. 合肥:安徽科学技术出版社, 1995: 43 FU Zhufeng, HU Youqiu. Numberical simulation of space plasma[M]. Hefei: Anhui Technology Press, 1995: 43

7 John Zinn, Herman Hoerlin, Petschek A G. The motion of bomb debris following the starfish test,.Radiation Trapped,Los Alamos Scientific Laboratory, 1967: 671–692