基于FPGA状态空间方程解算器的HIRFL-CSR电源控制器设计
2012-10-16乔卫民李桂花石顾可伟武俊奇姜子运
杨 锋 乔卫民 张 玮 李桂花 安 石顾可伟 武俊奇 姜子运 陈 云
1(中国科学院近代物理研究所 兰州 730000)
2(中国科学院研究生院 北京 100039)
数字PI控制的数字电源[1]在加速器技术中得到快速发展与应用,然而,电源控制时的动态性能及负载扰动抑制方面,尚存在不足。微处理器的发展使计算机功能日益强大,成本日益降低,使基于现代控制理论的许多复杂算法的实现成为可能。基于状态空间模型的最优状态反馈控制系统,可解决PI调节器响应速度慢、易出现超调的缺点,提高系统的响应速度与鲁棒性,且在完成多个状态反馈时也不会构成分立的多闭环控制系统。为实现以状态反馈为主的复杂算法,我们设计了基于ARM与现场可编程逻辑门阵列(FPGA)的电源数字控制器,并在FPGA中设计了适用于状态反馈控制系统的硬件状态空间方程解算器。通过上层软件对控制器参数的修改,便可控制不同磁铁电源输出电流的高速、高精度、高稳定性。
1 数字电源控制系统总体结构设计
电源控制系统由上层服务器、智能数字控制器、采样反馈电路、功率变换器、滤波器及负载等组成,整个数字电源控制系统如图1所示。

图1 电源数字控制系统硬件结构图Fig.1 Power supply control system hardware configuration.
考虑磁铁电源系统对精度、响应速度、远程控制、网络传输及进行高速复杂算法的要求,加速器电源控制系统要满足以下四点:(1) 拥有高速数据处理和实时、高精度的矩阵运算能力,并能够实现对五阶及五阶以下离散状态空间方程的实时求解;(2) 拥有高速、高精度的数据采集能力;(3) 高分辨率的数字 PWM 输出能力;(4) 能够实现良好的人机交互界面。因此,采用ARM+FPGA嵌入式结构的控制器(图2)。
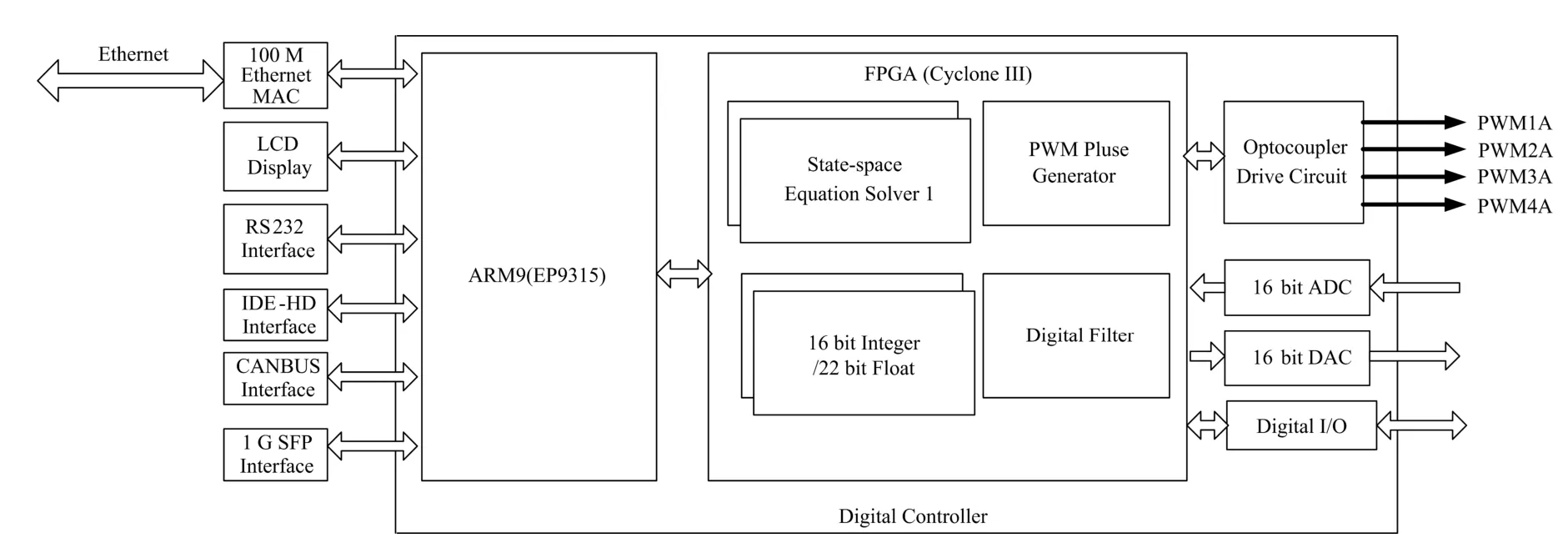
图2 状态空间控制器硬件结构框图Fig.2 Hardware block diagram of state-space controller.
数字控制器由ARM处理器及FPGA两大模块组成,另外配以高精度ADC/DAC模块、PWM输出通道以及数字通讯等外设。ARM选用ARM9系列的EP9315作为微处理器。主要运行嵌入式Linux操作系统,并在操作系统上完成系统的多线程任务处理,包括FPGA数控单元的数据传输、外界接口的扩展控制及并行完成网络通信、触摸屏接口驱动等任务。
高速、高精度 ADC是加速器电源数字化的关键技术,加速器电力电子开关元器件的开关频率高达20 kHz以上。若ADC采样频率小于5倍开关频率,控制器的调节效果就大打折扣,甚至完全失效。鉴此,选取AD7656作为控制器的模拟/数字采样设备,采样频率可达250 kHz,完全适应开关电源对高速采样的要求。
FPGA是整个控制器中完成电源闭环控制、进行控制算法的核心元件。为满足高速复杂算法的需求,选用Altera公司新一代低成本、大容量、高性能的Cyclone® III EP3C25F256 FPGA。其独特的体系结构及丰富的硬件逻辑资源,可设计高速浮点数状态空间方程解算模块、高精度PWM(pulse width modulation)波生成模块、数字滤波模块、ADC/DAC控制模块、定点转浮点及浮点转定点模块,FPGA中主要的功能模块组成如图3所示。r(k)为给定参考信号,y(k)为AD采样信号,FPGA将16位定点数格式的参考给定及经过数字滤波模块处理的 ADC采样信号转化为22位的浮点数,通过状态空间方程解算器的高速实时运算以及PWM波生成模块的处理,生成固定频率的PWM波形。

图3 FPGA系统结构原理框图Fig.3 FPGA block diagram.
上述结构的数字控制器,可实现对磁铁电源的各种状态反馈控制。对于不同负载,可通过上层操作界面修改控制器所需的参数,并通过网络接口将参数及电源基准信号传输给数字控制器。数字控制器经 1个运算周期后,输出控制量。控制量经过FPGA的PWM波形生成模块处理后,转换为高精度的PWM脉宽调制信号,以此控制H桥开关管的占空比,实现对电源输出电压或电流的闭环控制。
2 状态空间解算器在FPGA的实现
控制算法是影响电源性能的关键因素,图3 FPGA中的状态空间方程解算器是实现控制算法的关键。为实现基于现代控制理论的带观测器的状态反馈控制[2,3],并确保系统的跟踪性能及稳态精度良好,综合基于状态空间理论的各种状态反馈形式,我们用硬件描述语言VHDL,在FPGA中设计了硬件状态空间方程解算器:
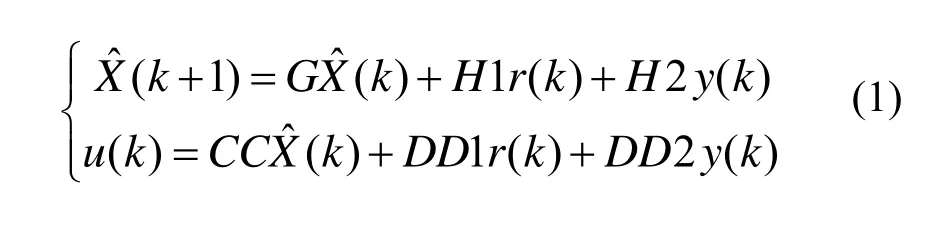
式中,G、H1、H2、CC、DD1、DD2为 FPGA状态空间方程解算器中的常系数矩阵,r(k)为参考输入信号,y(k)为系统的输出反馈信号,u(k)为系统的控制信号。为能实现五阶及五阶以下单输入、单输出系统的控制,我们将状态向量(k)的维数最大设计为5维,并在FPGA中实现大量的矩阵运算,包括:系数矩阵G(5×5矩阵)与状态向量ˆ(k)的矩阵浮点数乘加运算ˆ(k),系数矩阵H1(5×1矩阵)与输入r(k)的矩阵浮点数乘法运算H1r(k),系数矩阵H2(5×1矩阵)与系统输出y(k)的矩阵浮点数乘法运算H2y(k),系数矩阵CC(1×5矩阵)与状态向量矩阵ˆ(k)的矩阵浮点数乘加运算(k),系数矩阵DD1(1×1矩阵)与输入r(k)的浮点数乘法运算DD1r(k),系数矩阵DD2(1×1矩阵)与系统输出y(k)的浮点数乘法运算DD2y(k)。整个状态空间方程在FPGA中的矩阵运算流程如图4所示。
状态空间方程解算器中的常系数矩阵G、H1、H2、CC、DD1、DD2由上层参数设计程序配置,并通过网络接口传输到 FPGA固定的矩阵存储器中。当控制器接收到触发信号时,则开始根据给定输入及输出反馈信号进行高速的状态空间方程解算过程。由于解算器采用流水线技术,最终整个状态空间方程解算器在FPGA的解算周期为200 ns。实际电源为0型系统,为消除由于模型参数不准或阶跃型干扰引起的稳态误差,在控制器参考输入端引入一积分控制,整个电源控制系统结构如图5所示。

图4 状态空间方程解算器的数据流程图Fig.4 Data flow diagram of the state-space equation solver.
3 仿真及试验结果
为验证该控制器对电源系统的控制效果,由图1所示的试验平台,选取实验参数为[1]:平波电感Lf=0.68 mH,滤波电容C=30 μF,负载电阻R=0.766Ω,负载电感L=0.34 mH(实验负载为电抗器串联电阻),PWM模块输出频率设置为20 kHz。为简化试验过程,在满足输出功率、输出电压纹波、输出电压精度及稳定度的前提下,用直流稳压电源代替电压预稳电路,稳压电源输出电压Ut=15 V。设电源系统平均状态空间[4,5]方程为:

式中,X(k)为状态向量,y(k)为输出量,u(k)为控制量,A为状态矩阵,B为输入矩阵,C为输出矩阵。

图5 带积分控制的电源状态反馈控制系统结构框图Fig.5 Block diagram of the state-feedback control system with integral action.
对该电源进行线性二次型最优[2,3](LQR)状态反馈设计,在控制器算法中构造观测器,并在控制器参考输入前端引入了积分控制。利用现代控制理论的状态反馈设计方法,经过转换及计算,可得控制器的结构为:
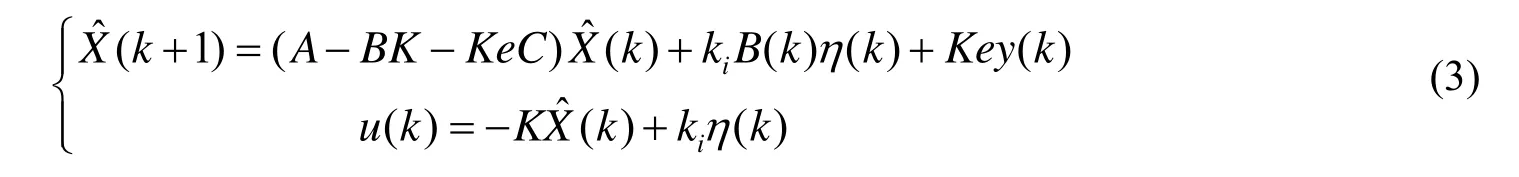
式中,K为利用LQR方法确定的系统状态反馈增益矩阵,Ke为状态观测器的增益矩阵,为积分增益常数。比较式(3)与式(1),可得状态空间解算器矩阵参 数 :G=A–BK–KeC,H1=kiB,H2=Ke,CC=–K,DD1=ki,DD2=0。
本文用Simulink和SimPower System工具箱[6],对上述电源控制系统进行仿真,其闭环系统动态特性曲线如图6所示。闭环系统在2 ms时,输出就可无静差地稳定于给定值。在4 ms时,将负载R由0.766 Ω瞬间跳变为1.266 Ω;在7 ms时,将输入电压Ui从15 V跳变为20 V,扰动幅度为20%以上,而系统在2 ms内可消除干扰影响,使负载端电压稳定在新的平衡点,并始终保持输出电流稳态值不变。
图7为电源在负载与输入电压发生阶跃性跳变时的测试结果。图7(a)为电阻发生跳变时的电源电流输出回读曲线,干扰在3 ms内消除;图7(b)为输入电压发生跳变时的电源电流输出回读曲线,干扰在2 ms内消除。由于实际电路参数与仿真参数有误差,响应时间有所差异,响应曲线与仿真基本一致。
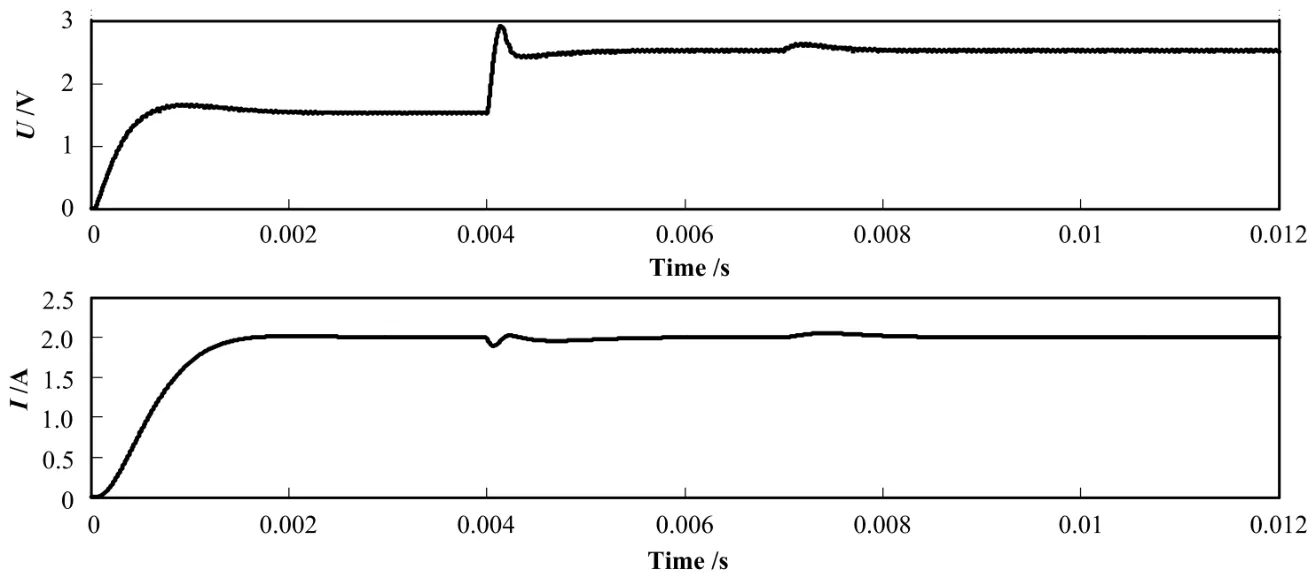
图6 状态反馈电源控制系统输出电压/电流的仿真动态响应曲线Fig.6 Transient response curve of the state feedback control system simulation.

图7 状态反馈电源控制系统输出电压/电流的试验动态响应曲线图Fig.7 Transient response curve of the state feedback control system.
4 结语
本文采用基于ARM+FPGA结构的全数字控制器,以带有状态空间解算器的FPGA作为控制器的核心,实现对开关电源高速、实时的状态反馈控制。其系统仿真及试验的结论以下:
(1) 基于FPGA状态空间方程解算器的最优状态反馈系统能够无静差地跟踪电源给定值,大大提高了开关电源的动态响应速度、稳态精度、抗干扰性及鲁棒性;
(2) 运用VHDL语言设计的基于FPGA状态空间解算器的数字控制器,可以很好地实现对五阶及五阶以下被控对象的观测-状态反馈闭环控制,这在加速器控制器的设计中是一种全新的尝试;
(3) 基于 ARM+FPGA的控制器集成度高,结构布局合理,适用性强,对于不同的电源负载,无需重新配置硬件,只需通过上层软件修改控制器的参数(G、H1、H2、CC、DD1、DD2)来满足指标要求,大大缩短控制系统设计的周期。
(4) 该控制器不仅可以在线修改控制参数,而且可根据不同的控制对象在线修改控制算法。使控制系统的设计主要集中在FPGA程序的设计上,为对加速电源进行智能控制等更复杂的控制系统设计奠定了基础。
该控制系统的研制与实现,将为加速器束流品质和运行效率的提高起到重要作用。在FPGA高速状态空间解算器的基础上,还可进一步进行自适应控制、智能控制等现代复杂控制策略的研究。期待在系统优化的基础上,对该控制器实现产品化及规模化,为加速器的发展作出贡献。
1 王进军. 加速器电源的数字化研究与设计[D]. 兰州:中国科学院近代物理研究所, 2010 WANG Jingjun. Digital Power Supply for Accelerator Researching and Design [D]. Lanzhou: Institute of Modern Physics, Chinese Academy of Sciences, 2010
2 Katsuhiko Ogata. Modern Control Engineering [M].Englewood: Prentice Hall, 2009: 64–66, 767–771
3 Katsuhiko Ogata. Discrete Time Control Systems [M].Upper Saddle River: Prentice Hall, 1995: 317
4 Sherif Hammad, Mentor Graphics. H1 field bus network delay, a digital pole placement control design[C].Proceedings of the 17thCongress of the International Federation of Automatic Control, Seoul, Korea, 2008,6-11: 9433–9436
5 Maksimovic. Automated small-signal analysis of switching converters using a general-purpose timedomain simulator. Applied Power Electronics Conference and Exposition, APEC'98, Conference Proceedings 1998,Thirteenth Annual, 1998, 1: 357–362
6 洪乃刚. 电力电子技术基础[M]. 北京: 清华大学出版社, 2008: 49–51 HONG Naigang. Fundamentals of Power Electronics [M].Beijing: Peking University Press, 2008: 49–51
