PHC管桩极限承载力影响因素敏感性分析
2012-10-16许旭堂吴能森崔广强龚灿宁肖勇杰
许旭堂,吴能森,崔广强,龚灿宁,肖勇杰
(1.福建农林大学交通学院,福建福州350002;2.福建农林大学金山学院,福建 福州350002)
当前,静压桩在我国各地区的用量越来越广泛,尤其是PHC管桩的应用更在各类桩型中占据明显优势[1]。基础工程的首要问题是稳定问题。研究表明,影响PHC管桩稳定性的因素包括桩长、桩径、入土深度、侧摩阻力和端阻力等[2-4],即桩基失稳的机理和模式与这些影响因素有密切的关系。我国有很多的学者利用桩基试验、纯数学理论和交叉学科等方法,建立了多种桩基承载力预测模型[5-9],但很少对影响桩基承载力的诸因素进行敏感性分析研究。诚然,根据规范的经验公式可以分析一些单因素对桩基承载力的影响,但实际上有些影响因素在经验公式中并未得到体现,而且各影响因素的敏感性也不尽相同。为此,根据实际工程的试桩资料,通过建立预测桩基承载力的GA-BP网络,结合正交试验设计法,对影响PHC管桩承载力的各主要影响因素进行敏感性分析。
1 神经网络和正交试验设计理论简介
1.1 BP 和 GA -BP神经网络[10]
BP神经网络是目前应用最广泛的人工神经网络,由输入层、隐层和输出层组成(图1)。输入层有n个输入信号,每个输入信号用小圆圈(圆圈也代表神经元)表示,输出层有一个输出信号,输入与输出层的节点数根据具体问题而定,一般情况下隐含层个数m(m=2n+1)。层与层之间的节点通过权值调节,各神经元之间的数据变换函数一般为Sig-moid函数。
然而BP算法在应用中暴露出不少内在的缺陷,如容易形成局部极小而得不到全局最优,学习效率低,收敛速度慢;训练时学习新样本有遗忘旧样本的趋势。因此,可以通过遗传算法来对BP神经网络的权值、阈值进行优化,即GA-BP神经网络,然后再用BP算法训练网络,将初步得到的权值矩阵赋给尚未开始训练的BP网络。

1.2 正交试验设计理论[11]
正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验的,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水平组合。
正交表是正交试验的分析工具,它具有正交性、代表性和综合可比性3种性质。具体表现在:(1)任一列的各水平出现的次数相等;任两列间所有水平组合出现次数相等;(2)任一列或任两列的各水平都出现,确保部分试验中包括了所有因素的所有水平,使得任意两因素间的试验组合为全面试验。因此用正交表安排的试验,具有均衡分散和整齐可比的特点。
2 单桩承载力影响因素敏感性分析
2.1 GA-BP网络和正交试验模型
根据文献[2~4] ,影响PHC单桩竖向承载力的主要因子可归纳为:桩径、桩长、入土深度、侧摩阻力、端阻力、压桩力、渗透系数和休止期,即网络的输入层节点数n=8,隐含层节点数m=17,而输出层为单桩极限承载力值,节点数k=1,则网络结构为8-17-1。采用浮点数编码方式,每个个体均为一个实数串,个体包含了神经网络全部权值和阈值。在网络结构已知的情况下,就可以构成一个结构、权值、阈值确定的神经网络。遗传算法编码长度S(S=n×m+m×k+m+k)为171。个体适应度值可取预测输出和期望输出之间的误差绝对值之和,经多次验算得到较优的网络参数为:种群规模50,遗传代数100,交叉概率 Pc取0.4,变异概率 Pm取0.1,动量参数取0.1,学习率取1.05。
选定8个影响因素,各因素的位极水平为7个(表 1),选用正交表为 L49(78)[11]。
2.2 应用实例及分析
2.2.1 工程算例
选用福建某地区实际工程的58根PHC管桩的相关数据进行神经网络学习。采用带动量项的GA-BP网络进行训练,经过1239步学习收敛,精度达0.01,训练误差随训练次数变化曲线见图2。训练好的网络确定了各输入、输出层间的权重和阈值。
以该地区具有代表性的土层(淤泥层和残积粘性土层都比较厚)和比较常用的PHC500-100管桩(88#工程桩)为例,其相关参数见表1。基本数据按照表1的位极进行组合后形成49组样本,用已经训练好的GA-BP网络对组合样本进行试验,输出的单桩极限承载力值见表2。把相同水平下的各因素的均值作为每个因素在不同水平下的预测值,反映各因素变化情况的极差值为同一因素不同水平下均值的最大值与最小值之差,结果如表3所示。由于各因素变化的范围在同一幅度内,所以极差的大小就代表敏感性的大小。由表3可见,影响单桩竖向极限承载力的因素敏感性排序为:桩径、桩侧摩阻力加权平均值、休止期、桩长、入土深度、渗透系数和终止压桩力,其中桩径和桩侧摩阻力值的影响最为敏感,其次是休止期。

2.2.2 结果分析
桩的极限承载力Qu由桩侧极限阻力Qsu和桩端极限阻力Qbu组成,设桩侧单位平均极限侧阻力为,桩端单位极限阻力为qpu,则Qu可表示为:

式中:d-桩径;l-桩长;Ap-桩截面积。
由表1可知,工程桩的长径比l/d为61.7~63,介于40和100之间,属于长桩。桩顶竖向荷载,随着l/d的增大,传递到桩端的荷载减小;对均匀土层中的长桩,桩顶竖向荷载基本由桩侧阻力承担,桩端阻力分担的荷载趋于零[12]。上述工程桩的土层不均匀,上部为淤泥层,下部残积粘性土层,由于上部淤泥层的极限侧阻力有限,而下部的残积粘性土层的侧阻力不能完全发挥,因此端阻力的敏感性很弱,即也就是说,在长径比l/d一定的条件下,Qsu分别与桩径d的平方及桩侧单位平均极限侧阻力成正比。
淤泥和残积粘性土都具有很强的结构性,在压桩过程中受扰动强度降低,但成桩后会随着间歇时间(休止期)而得到逐步恢复[12-13],从而使成桩的侧阻力增加,因此休止期对Qu的影响也比较敏感。桩长和入土深度对Qu的影响主要表现在l/d上,由于本工程桩属于长桩,且l/d值基本恒定,因此其敏感性的影响不突出;渗透系数大小会影响孔隙水压力的消散,影响桩侧土的固结度,进而影响桩侧极限阻力,但由于本工程桩侧土的渗透系数在 0.642 ×10-6~1.284 ×10-6cm/s范围内,属于弱透水性,在较短的6~12 d休止期内,孔压消散不明显,因此其敏感性也很弱。至于终止压桩力,由于压桩过程的扰动和破坏作用,桩侧阻力小,终止压桩时其阻力以桩端坚硬土层或岩层的阻力为主,这与工程桩的实际承载性状差异很大,因此其相关性差,敏感性最弱。
3 结语
1)对桩侧以淤泥层和残积粘性土层为主,承载性状为端承摩擦型的PHC管桩,其影响单桩竖向极限承载力因素的敏感性排序为:桩径、桩侧摩阻力加权平均值、休止期、桩长、入土深度、渗透系数和终止压桩力。

表1 因素位极组合表Tab.1 The combination table of factor levels
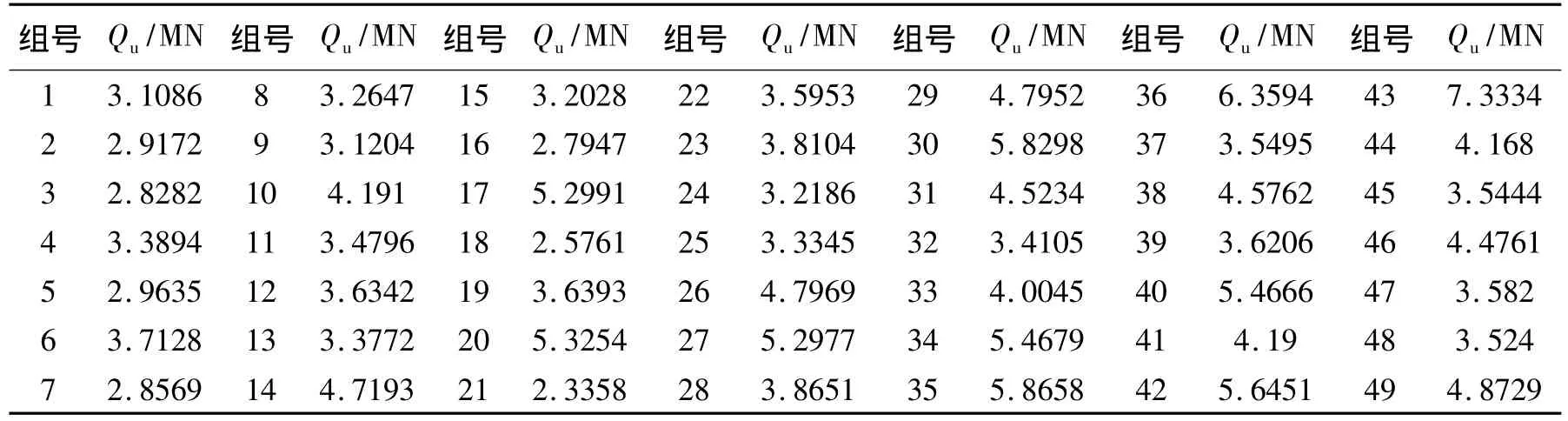
表2 极限承载力正交试验结果汇总Tab.2 The summary of ultimate bearing capacity of orthogonal test results

表3 单因素变化对应的极限承载力(MN)Tab.3 The ultimate bearing capacity corresponded with single factor changing unit:MN
2)桩径和桩侧摩阻力值对单桩竖向极限承载力的贡献最大,而休止期的影响仅次二者,也很显著。这点有时往往不为人们所重视,甚至忽视时间效应的影响,盲目提前试桩时间,会影响试桩结果。
3)采用GA-BP神经网络,结合正交试验设计法分析影响桩基承载力因素的敏感性,能够有效地对BP神经网络的权值、阈值进行优化,克服了BP算法的内在缺陷,而且能有效的节省计算工作量,具有实用价值。
[1] 张明义.静力压入桩的研究与应用[M] .北京:中国建材工业出版社,2004.
[2] 马利耕.开口型预应力混凝土管桩竖向承载力分析[D] .哈尔滨:哈尔滨工程大学,2009.
[3] 张明义,时伟,王崇革,等.静压桩极限承载力的时效性[J] .岩石力学及工程学报,2002,21(增2):2601-2604.
[4] 张雁,刘金波.桩基手册[M] .北京:中国建筑工业出版社,2009.
[5] 朱守鹏,刘齐茂.桩-土-结构相互作用研究综述及展望[J] .四川理工学院学报:自然科学版,2011,24(3):253-257.
[6] 律文田,王永和,冷伍明.PHC管桩荷载传递的试验研究和数值分析[J] .岩土力学,2006,27(3):466-470.
[7] 左宏亮,刘景云,李国东,等.松花江漫滩地区静压PHC管桩竖向承载力[J] .沈阳建筑大学学报,2009,25(6):1088-1093.
[8] 李万庆,李铮.基于熵权法的PHC管桩承载力组合预测[J] .河北工程大学学报:自然科学版,2011,28(1):64-67.
[9] 卓维松.泉州市区PHC桩竖向抗拔极限承载力预测[J] .河北工程大学学报:自然科学版,2011,28(2):14-18.
[10] 袁曾任.人工神经网络及其应用[M] .北京:清华大学出版社,1999.
[11] 陈魁.试验设计与分析[M] .北京:清华大学出版社,2005.
[12] 莫海鸿,杨小平.基础工程[M] .北京:中国建筑工业出版社,2008.
[13] 吴能森.结构性花岗岩残积土的特性及工程问题研究[D] .南京:南京林业大学,2005.
