破圈法应用中的误区分析

闫超君

(安徽水利水电职业技术学院，安徽合肥231603)

工程实践中，常用双代号网络图表达工作之间的相互关系和整个工程任务的全貌，通过分析计算，找出对全局有决定性影响的关键线路和各项关键工作，据此对任务作出切实可行的全面规划和安排。确定双代号网络图关键线路的方法有很多，诸如:直接法、总时差最小法、节点参数法、时标网络图法、标号法、破圈法。其中破圈法运用时不需大量计算，是一种比较简便直观的方法，但由于在运用破圈法时，有一些误区存在。为此，在实际工作中很少有人运用，使得破圈法应用不是很广泛。

1 对破圈法的初步认识

在双代号网络图中有许多节点和箭线，这些节点和箭线形成了许多封闭的“圈”，这些“圈”是指在两个节点之间由两条线路连通该二个节点所形成的最小圈。破圈法是将网络中各个封闭圈的二条线路按各自所含工作的持续时间来进行比较，破掉持续时间短的线路，逐个“破圈”，直至圆圈不可破时为止，最后剩下的线路即为网络图的关键线路如图1。

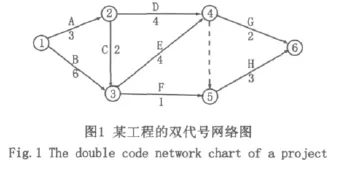
从节点①开始，节点①、②、③形成了第一个圈，从节点①到节点③有二条线路，一条是①→③，一条是①→②→③。①→③需要时间是6，①→②→③需要时间是5，因6﹥5所以切断①→②→③。

从节点②开始，节点②、③、④形成了第二个圈，从节点②到节点④有二条线路，一条是②→③→④，一条是②→④。②→③→④需要时间是6，②→④需要时间是4，因6﹥4所以切断②→④。

从节点③开始，节点③、④、⑤形成了第三个圈，从节点③到节点⑤有二条线路，一条是③→④→⑤，一条是③→⑤。③→④→⑤需要时间是4，③→⑤需要时间是1，因4﹥1所以切断③→⑤。

从节点④开始，节点④、⑤、⑥形成了第四个圈，从节点④到节点⑥有二条线路，一条是④→⑤→⑥，一条是⑤→⑥。④→⑤→⑥需要时间是3，④→⑥需要时间是2，因3﹥2所以切断④→⑥。剩下的即为关键线路，见图2所示中的双箭线。

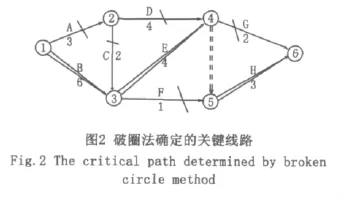
2 误区分析

上述示例看似正确，但有不少误区存在。比如按上述方法确定图3所示的双代号网络图，关键线路就确定不出来，甚至判断出错误的关键线路。

按上述所述破圈法，从节点①开始，节点①、②、③形成了第一个圈，从节点①到节点③有二条线路，一条是①→③，一条是①→②→③。①→③需要时间是2，①→②→③需要时间是3，因3﹥2所以切断①→③。

从节点①开始，节点①、③、④、⑤形成了第二个圈，从节点①到节点⑤有二条线路，一条是①→③→⑤，一条是①→④→⑤。①→③→⑤需要时间是4，①→④→⑤需要时间是7，因7﹥4所以切断①→③→⑤。

同理可切断⑦→⑧，④→⑧。关键线路如图4双箭线所示。但是，用此方法判断出的关键线路是错误的。正确的关键线路如图5双箭线所示。

出现破圈法判别的关键线路不正确的原因就是大家对破圈法的错误理解，判断中存在误区，现分析一下存在的误区。

误区一:破圈时，去掉一整条线路。凡遇到节点有两个及两个以上的内向箭线时，肯定有一个圈，比较时间长短，把时间较短线路流进的一个箭线去掉，如图6所示只去掉②→③，误区是把整条线路去掉如图7所示，去掉了①→②箭线和①→③箭线。

误区二:破掉的箭线，找下一个圈时还在用。破圈法找圈时，破掉的箭线不能再次用，误区是去掉的箭线还继续用。图4中到⑤节点有两个内向箭线，一定有个最小的圈，此最小的圈不是由①→③→⑤和①→④→⑤两条线组成的圈，因为①→③已破掉，而是由①→②→③→⑤和①→④→⑤两条线组成的圈。图4中到⑦节点有两个内向箭线，一定有个最小的圈，此最小的圈不是由②→③→⑤→⑦和②→⑥→⑦两条线组成的圈，因为③→⑤已破掉，而是由①→②→⑥→⑦和①→④→⑤→⑦两条线组成的圈。

误区三:破圈法不能判别所有双代号网络图的关键线路。由于不能正确地找到“圈”，就不能正确地破“圈”，以至于双代号网络图利用破圈法确定关键线路，破到最后，连一条完整的线路都没有，就不能确定出关键线路，于是认为，破圈法不科学，不好用，不能判别所有双代号网络图的关键线路。正是因为此原因，很多教科书上都不介绍破圈法。实际是所有的双代号网络图都可以用破圈法判别出关键线路。

3 正确利用破圈法确定关键线路

通过对破圈法的再认识，走出误区，正确判别双代号网络图的关键线路。对图3所示网络图进行破圈法判别关键线路。

从节点①开始，到③有两条内向箭线，节点①、②、③形成一个圈，即从节点①到节点③有二条线路，一条是①→③，一条是①→②→③。①→③需要时间是2，①→②→③需要时间是3，因3﹥2所以切断①→③。

到节点⑤有两条内向箭线，但①→③箭线已被断开，所以节点①、③、④、⑤不能形成一个圈，应扩大范围找“圈”，节点①、②、③、④、⑤形成一个圈，即从节点①到节点⑤有二条线路，一条是①→②→③→⑤，一条是①→④→⑤。①→②→③→⑤需要时间是5，①→④→⑤需要时间是7，因7﹥5所以切断③→⑤。

到节点⑦有两条内向箭线，由于③→⑤已破掉，所以节点②、③、⑤、⑥、⑦不能形成一个圈，应扩大范围找“圈”，节点①、②、④、⑤、⑥、⑦形成一个圈，即从节点①到节点⑦有二条线路，一条是①→②→⑥→⑦，一条是①→④→⑤→⑦。①→②→⑥→⑦需要时间是8，①→④→⑤→⑦需要时间是10，因10﹥8，所以切断⑥→⑦。

到节点⑧有三条内向箭线，一定有两个圈，节点④、⑤、⑦、⑧形成一个圈，即从节点④到节点⑧有二条线路，一条是④→⑤→⑦→⑧，一条是④→⑧。④→⑤→⑦→⑧需要时间是7，④→⑧需要时间是5，因7﹥5，所以切断④→⑧。由于⑥→⑦已破掉，节点⑥、⑦、⑧不能形成一个圈，应扩大范围找“圈”，节点①、②、⑥、⑧、④、⑤、⑦形成一个圈，即由①→②→⑥→⑧，和①→④→⑤→⑦→⑧这两条线形成另一个圈，①→②→⑥→⑧需要时间是13，①→④→⑤→⑦→⑧需要时间是14，因14﹥13，所以切断⑥→⑧，如图8所示。

剩下的线路，能从起点走到终点的线路就是关键线路，①→②→⑥走不通，不是关键线路，①→④→⑤→⑦→⑧从起点走到了终点，故是关键线路，如图8双箭线所示。

从图8可以看出，关键线路与标号法确定的关键线路(图5)一致。

4 结束语

通过对破圈法的误区分析，运用破圈法时注意三原则:破最小的圈、破过的线)不可以再用、只破流进箭线的一个箭线。走出误区，就能快速地运用破圈法判别双代号网络图的关键线路，而且所有的双代号网络图都可以用破圈法确定关键线路。

破圈法不需计算时间参数，通过破圈就可以确定出关键线路，简单直观，是一种非常实用的确定双代号网络图关键线路的方法。

［1] 闫超君.建设工程进度控制［M] .合肥:合肥工业大学出版社，2009.

［2] 庞素珍.用图论理论正确掌握破圈法［J] .河北北方学院学报，2007(5):80－82.

［3] 董跃华，李云浩.用破圈法实现普利姆算法［J] .江西理工大学学报，2008(4):20－21.

［4] 郭月明.运筹学［M] .广州:华南理工大学出版社，2001.

［5] 李济民.用图论指导破圈法的学习［J] .经济与管理，1998(1):42－43.

［6] 周 迎.破圈法解动态规划中的最短路问题［J] .西昌农业高等专科学校学报，2003(3):68－69.