基于LXF模型水平集的玉米叶部病斑图像分割

2012-10-16张柏毅朱景福

黑龙江八一农垦大学学报 2012年3期

张柏毅，朱景福

（黑龙江八一农垦大学信息技术学院，大庆163319）

近年来，我国已经进入实现农业现代化与自动化关键阶段，而玉米又是我国的主要粮食作物之一，仅次于水稻与小麦，所以利用图像处理和识别技术来实现玉米叶部病斑识别对玉米作物病害治理起到了推进作用。然而对图像的准确分割决定着对后期图像识别工作的质量，所以对玉米叶部病斑图像的分割成为了实现玉米叶部病斑识别的重点，由于玉米叶部病斑部位与背景区域有着明显的区别，因此可以采用基于LXF模型水平集图像分割的方法进行对玉米叶部病斑图像的处理。

在1988年，Sethian和Osher提出了水平集算法（Level Set）[1]，该算法在近几十年被许多专家运用和改进并加以推广。简单地说来，它是把低维的一些计算上升到更高一维计算的一种方法，相当于把N维的扩展到N＋1维的一个水平[2]，并且运用符号距离函数来规范在演化过程中水平集函数的变化。在研究该算法过程中，许多专家学者提出了很多方法来达到水平集的重新初始化的目的[3]。但是大多数方法都是利用水平集函数迭代的过程来对一个偏微分方程求解来实现水平集的重新初始化，因此产生了大量的计算。为解决该问题，Chan和Vese将Mumford-Shah函数[4-5]引入了水平集算法当中而且通过改进成为了一种可以变分的水平集算法（Chan-Vese算法）[6]，这种方法实现了对影像进行分段线性的影像分割，它将影像分割转化为影像的优化问题，影像的边缘部分可以不像以往的水平集再用梯度值来代表描述，可以利用使能量最小化的函数来得到影像中最优的分段线性值，相对零水平集的曲线就可以停止在影像的突出边缘上，但是曲线的演化速度上并没有明显的优势。

1 传统的水平集方法

水平集方法主要是处理图像中连续函数表示成曲面φ（x，y，t），并且将一种闭合平面曲线隐含的描述变化成为与其相同函数值的曲面。在一般情况下，用零水平集函数作为初始函数来描述初始目标曲线。

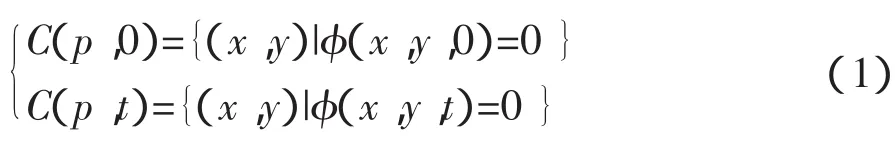
将平面闭合的演化曲线表示成为 C（p，t）=（x（p，t），y（p，t）），该公式中代表 p 在时间 t内任意参数化变量。

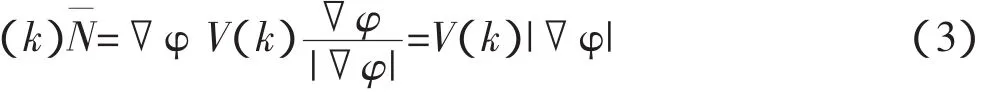
此公式就表示水平集曲线开始演化的方程。

用水平集的方法实现主动轮廓线模型有如下优点：

（1）演化曲线的拓扑结构可以随着φ的演化而改变，在此过程中，演化曲线可以进行分裂、合并和形成尖角等变化。

（2）由于φ在演化过程中始终保持为一个完整的函数，因此容易实现近似数值计算。

（3）对于三维分割的理论与应用的复杂性上，可以通过利用水平集的方法进行高维曲面的演化。

2 基于LXF模型水平集算法

在运用第1小节介绍的传统的水平集方法过程中，一般将初始水平集函数用初始曲线计算的符号距离函数代替，公式为：

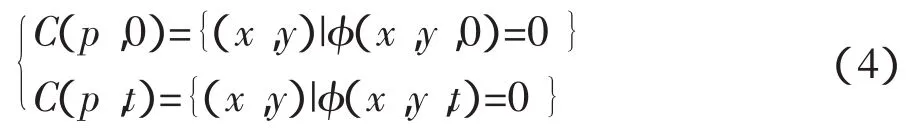
当水平集函数不能用符号距离函数表示，就是可能在迭代的过程水平集函数发生了退化，所以必须重新初始化水平集函数，这是为了重新将水平集函数用符号距离函数代替，这样使得此数值解法保持稳定。

利用对Hamilton-Jacobi方程的计算可以标准地对水平集函数进行重新初始化，实现公式如下：

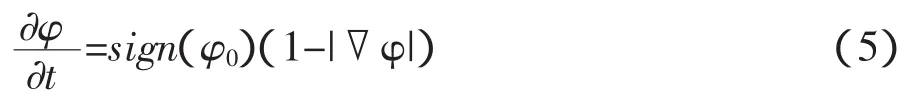
然而对水平集重新初始化成符号距离函的计算量较大，是由于演化的过程对水平集函数的校正是利用周期性操作的。可以利用LXF模型中将主动轮廓模型的水平集中加入距离约束的信息来解决此问题，也就是说不用进行重新初始化水平集函数就可使水平集函数趋近于符号距离函数，这种方法优势很大，可以减少计算量从而节约计算时间。

要达到快速驱使初始水平集向景物的边界靠拢的目的，要在建立数学模型之前可以先将边缘检测函数引入进去，数学表示如下：

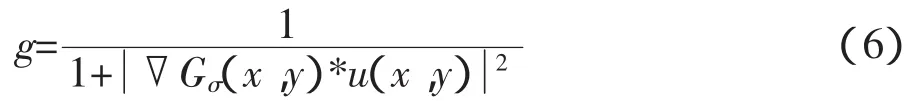
由上面公式可以得出下面的模型：

其中p是关于φ的内部能量函数，该项使水平集函数演化为符号距离函数。μ>0是内部能量项的权值；Em（φ）是一个控制水平集函数φ零水平集的外部能量项。

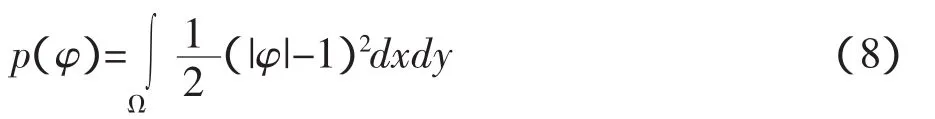
同时，可以定义外部能量项为：

初始水平集的曲线长度为：

目标区域的加权面积值：

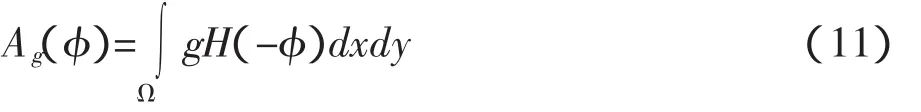
相关水平集演化的数学表示如下：

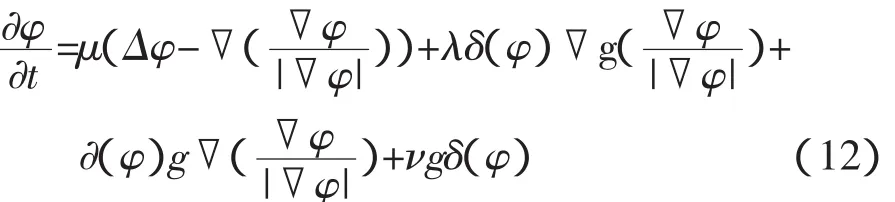
水平集演变的过程里不需要对该模型进行重新初始化，是由于内部含有受约束的内部能量项，这样简化了数学模型的计算，其中运用中心差分格式来逼近和近似公式（12）中的水平集的函数空间偏导数数值和。前向差分格式来近似逼近（时间偏导数），并且取较大的迭代步长，因此曲线演化就得到了加快。

3 玉米叶部病斑图像分割实验

应用Matlab R2010a编程。传统水平集分割如图组1、2所示，基于LXF模型水平集分割待分割玉米叶部病斑图像如图组3、4所示，在内外轮廓能量的作用下零水平集逐渐接近玉米叶部病斑直至达到稳定状态。

图1 （a）分割前图像Fig.1（a）Image before segmentation

图1 （b）水平集稳定图像Fig.1（b）The level set stable image

图2 （a）分割前图像Fig.2（a）Image before segmentation

图2 （b）水平集稳定图像Fig.2（b）The level set stable image

图3 （a）分割前图像Fig.3（a）Image before segmentation

图3 （b）水平集稳定图像Fig.3（b）The level set stable image

图4 （a）分割前图像Fig.4（a）Image before segmentation

图4（b）水平集稳定图像Fig.4（b）The level set stable image

图1 、2所选取的参数为 μ=0.1；υ=0；λ1=λ2=1；τ=0.5；ε=10。图组3、4所选择的参数为 μ=0.04；λ=5；υ=1.5；σ=1.5；ε=1.5；τ=3。

经过试验结果时间对比如列表1所示：

表1 处理时间对比表Table1 Contrast table of processing time

表1表明，在相同迭代次数下图3比图1的曲线演化速度快，水平集的生成效率更高，图4比图2的曲线演化速度快，水平集的生成效率更高。在图1（b）、图2（b）中的活动曲线并没有接近病斑边缘，图3（b）、图4（b）中的活动曲线变化在病斑边缘已经达到平稳状态。

玉米叶部病斑分割图像如图5所示：

图5 （a）病斑部位图像Fig.5（a）Disease spot image

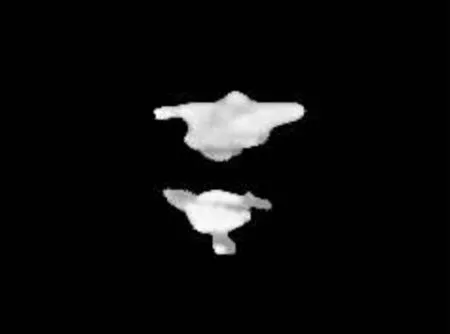
图5（b）病斑部位图像Fig.5（b）Disease spot image

图5 表明，运用基于LXF模型水平集算法对玉米叶部病斑进行分割，基本实现把病斑区域与玉米叶分割开来，玉米叶部病斑分割已经较明显，但是由于采集的玉米叶图像噪声影响，分割效果并不是完全准确，病斑周围还存在着小面积的玉米叶，原因是由于引入了梯度因子，所以对噪声还有一定的敏感性。

4 结论

基于LXF模型水平集算法由于加大了迭代步长，明显地缩短了解偏微分方程的时间，加速了曲线的演化速度；水平集不用初始化为特定的符号距离函数，可以根据需要灵活地设定，这样水平集的生成效率更高；该模型可以使用有限差分法简单实现，而不用以前模型中的逆风（upwind）算法[7]。玉米叶部病斑部位分割的较明显，基本可以描述玉米叶部病斑的特征，但是对于抗噪声有待提高，可以结合其他方法进一步处理，该方法为以后的病斑特征提取、病斑种类的识别打下了良好的基础。

[1]Osher S，Sethian JA.Fronts propagating with curvature dependent speed：Algorithms based on Hamilton-Jacobi formulation[J].Journal of Computational Physics，1988，79（1）：23-37.

[2]Osher S，Fedkiw R.Level Set Methods and Dynamics Implicit Surfaces[J].Springer-Verlag，2003，45（1）87-99.

[3]Peng DP，Merriman B，Osher S，et al.A PDE based fast local level set method[J].Journal of Computational Physics，1999，155（2）：34-45.

[4]Sethian J.Level setmethods and fast marching methods：evolving interfaces in computational geometry，fluid mechanics，computer vision，and materials science.Cambridge[J].Cambridge University Press，1999，131（1）：54-66.

[5]Mum ford D.，Shah.J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Commun.Pure Appl.Math，1989，12（1）：136-141.

[6]Chan TF,Vese LA.Active Contours Without Edges[J].IEEE Trans.on Image Processing，2001，10（2）：33-46.

[7]Chan TF，Vese LA.Active contours without edges[J].IEEE Trans.on Image Processing，2001，10（2）：266-277.