东北夏季Venlo型温室温度的时间预测模型构建与检验

韩跃，汪春

（黑龙江八一农垦大学工程学院，大庆163319）

东北地区属东亚季风气候区，地处中高纬欧亚大陆的东岸，是中国的老工业基地和最大的商品粮食基地。由于全球气候变暖，东北地区夏季气温不仅仅表现在平均气温的升高，气候变率也在增大，自1986年后，东北地区夏季气温升高显著[1-3]。尤其近两年来，东北地区夏季7月份平均气温达24℃以上，最高气温可达30～34℃。而作物生长的适宜温度在28℃以下，当外界气温达到25℃时，温室自然通风情况下的气温一般都在32℃以上，远远超过了作物生长的适宜温度[4]。

Venlo型温室，是一种源于荷兰的小屋面双坡面玻璃温室[5]，我国为发展设施农业建设，已在许多地区引进应用。近年来东北地区夏季气温升高，如何经济有效的降低温室内的温度是保证作物安全越夏生长并提高温室生产效率的重要环节。

为了更好地提高东北夏季温室的生产效率，通过测定温室内空气温度及其影响因素数据，对Venlo型玻璃温室温度建立了时间序列模型，可对温室温度进行预测，可为夏季东北Venlo型玻璃温室生产提供理论依据，提高农业信息化水平[6]。

1 材料与方法

1.1 实验材料

试验以黑龙江八一农垦大学的Venlo型玻璃温室为研究对象，运用JTJW-2建筑热工温度与热流巡回检测仪，测温传感器为铜-康铜热电偶。Venlo型玻璃温室南北走向，东西长24m，双屋脊跨度为8.4m，顶高5m。Venlo型玻璃温室具备交错式顶开窗，双跨具备6扇顶窗，每扇小窗长3 m，宽1 m，顶窗关闭时与地面夹角约为30度，温室顶部覆盖材料为4mm厚浮法玻璃，四周覆盖材料为6mm厚浮法玻璃。Venlo型玻璃温室南面侧墙配备连续型铝合金侧开外翻窗，长8m，宽1m，室内配备长8m，高1.5 m的湿帘机构，东墙配备两个风机，长宽均为1.4 m。系统布置了18个均匀的温度测点，东西走向划分了3个平面，一个面上各安置6个测点，其中纵向测点分别距地1.2m和2.4m。大棚结构及室温测量的布点位置如图1。试验时间为2011年7月9日-2011年8月24日，主要采集温室内的空气温度，及气象站采集的室外温度，风速，湿度，太阳辐射，记录时间间隔为1 h。期间无遮阳并保持自然通风，即顶窗和侧窗保持开启，风机每天8：00～17：00开启，并根据天气情况，手动开关湿帘降温系统，运用LM8000四合一风速仪检测风机风速及通过湿帘后的湿帘表面空气温度。

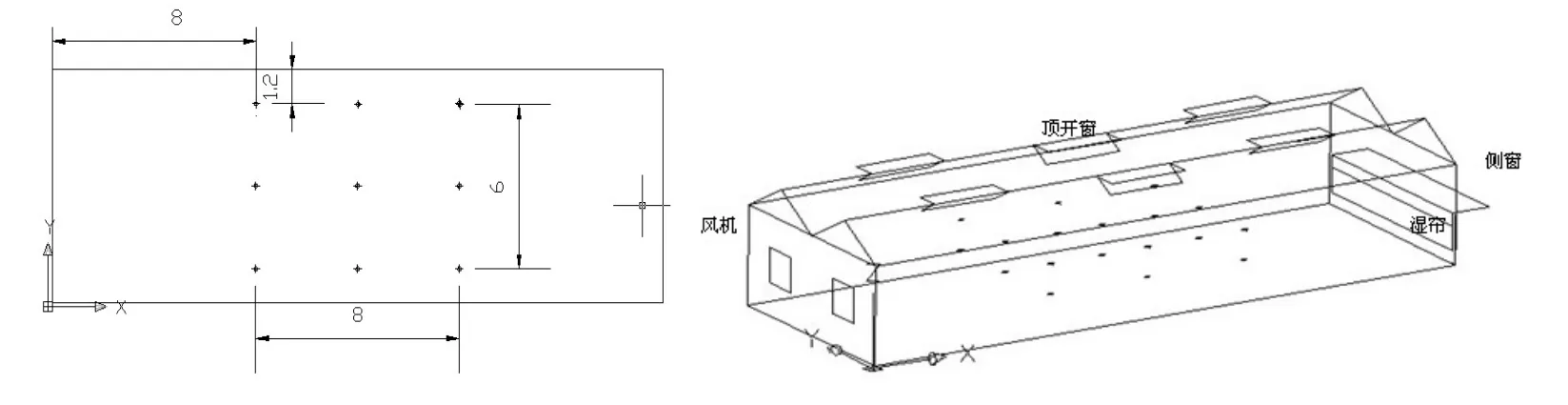
图1 温室结构及布点位置图Fig.1 Locationmap of the greenhouse structure and the distribution point

1.2 建模方法

温室环境控制系统以等时间间隔采集到的温度及其他各变量数据，是按照时间次序排列的一系列数据，这些数据记录序列是多组独立的时间序列[7]。因此对Venlo型玻璃温室温度的预测模型建立，采用时间序列分析方法。具体步骤如下[8-9]:（1）对通过实验测得的温室温度及其影响因素的原始数据序列，进行线性差值法处理异常、缺失的数据。（2）温室无遮阳下三种降温状态，即自然通风状态、自然通风+风机排风状态、自然通风+风机排风+湿帘降温状态，分别对各状态下的温室温度、HOBO气象站数据、自然通风率、风机开启时的总通风率、湿帘开启时经过湿帘表面的空气温度对序列进行ADF检验（单位根检验），检验是否为平稳序列。如果不是，则再进行一次一阶差分，然后再进行平稳性检验；如果是平稳序列，则根据自相关系数估计值和偏相关系数估计值选择模型类型。（3）对差分后的平稳时间序列进行协整检验并进行模型预估。（4）对估计的预测模型进行误差修正。（5）进行模型诊断检验和预测精度评价。

2 温室温度预测模型构建

2.1 异常与缺失数据的补足

异常点（outliner）是指一个时间序列观测中，远离序列一般水平的极端大值和极端小值，有时称为离群点或野值。将异常点去掉，便形成了缺省值，而由于数据采集时，也会由于仪器故障，操作失误等原因造成缺省值[10]。异常点检验与缺省值补足方法如下：

假定正常数据的序列值｛Xt｝是平滑的，而异常点是突变的，若

2.2 平稳性检验

室外温度TWw（℃）、室外太阳辐射强度RWw（w/m2）、自然通风速率V1（m3/s2）、风机开启时的总通风速率V2（m3/s2）、室外空气相对湿度SWw（%）以及通过湿帘降温的湿帘表面空气温度Ts（℃），这些是影响室内空气温度T（℃）的主要因子，其他因素均包含在随机误差项δ中引入模型，Venlo型玻璃温室无遮阳下三种降温状态，即自然通风状态、自然通风+风机排风状态、自然通风+风机排风+湿帘降温状态，分别可以表示为：

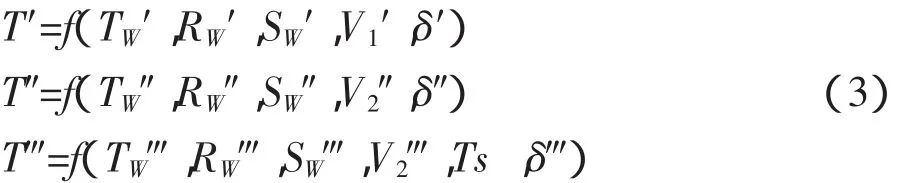
其中Venlo型玻璃温室自然通风状态下的通风速率[11]（V1，m3/s2）为：

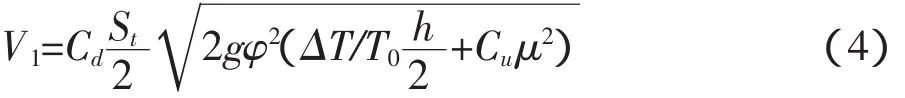
式中，h为进风口中心和出风口中心的垂直距离（m），TW为室外空气温度（℃）；ΔT为室内外温度差（ΔT=TWW-T），TW为室内温度（℃）;uW为室外风速；g为重力加速度（m/s2）；Cd，Cu分别为流量系数和综合风效系数，分别为0.64，0.09；St（m2）为顶窗开启面积（Sh）和侧窗开启面积（Sl）之和，φ因子表示为：

式中b=Sh/Sl=2.25，经计算φ≈1，温室内自然通风速率表示为：

当室外风速大于2m·s-1时，温室内自然通风速率可表示为：

试验期间，风机排风时间均在8：00～17：00间，所以期间总通风率为风机排风速率与自然通风速率之和，其中风机排风速率约为每单位秒下的风机面积与风机风速的乘积，经测试，风机风速约为6 m·s-1，所以计算得，风机排风速率为V2=9.23m3/s2。

式（3）中各变量若均为平稳序列，则根据自相关系数估计值和偏相关系数估计值选择模型类型。如果各变量是不平稳序列，对非平稳的时间序列建模会产生伪回归现象[12]，因此需要对各变量进行平稳性检验。

如果，经检验非平稳的时间序列Zt的自回归模型中含有单位根，其自回归模型为：

式（8）中λ是序列Zt的重要构成部分，εt是具有方差为σε2和零均值的独立同分布的序列，Φi为Zt的自回归系数。方程（4）可简化为3个模型:①λ具有常数项C（model“C，NT”）；②λ具有常数项C，趋势项T（model“C，T”）；③Zt不含λ（model“NC，NT”）。

表1 单位根检验的临界Table1 Criticality of the unit root test

运用eviews进行ADF单位根检验结果如表1，表2。经结果显示：各变量检验统计量值均有小于相应临界值，从而拒绝原假设，均不含单位根，即均是平稳的时间序列。

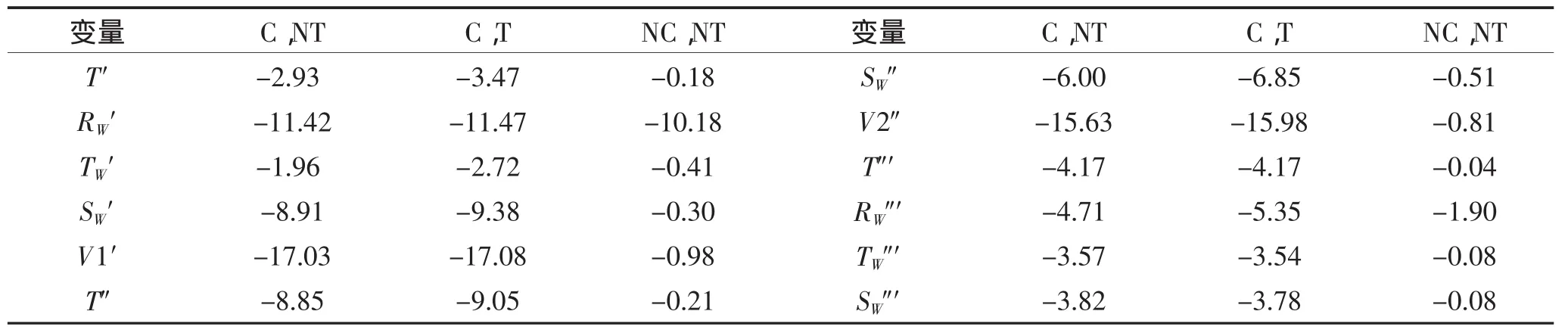
表2 单位根检验结果（t-统计量）Table2 Results of the unit root test（t-statistic）

2.3 选择模型类型

2.3.1 自相关检验和模型识别

温室自然通风状态下，根据方程回归残差的相关图和Q统计量，判断出ARMA模型的自回归过程可能是2阶，移动平均过程MA是低阶的。因此，估计下列两种模型形式：ARMA（2，1）和ARMA（2，2）。

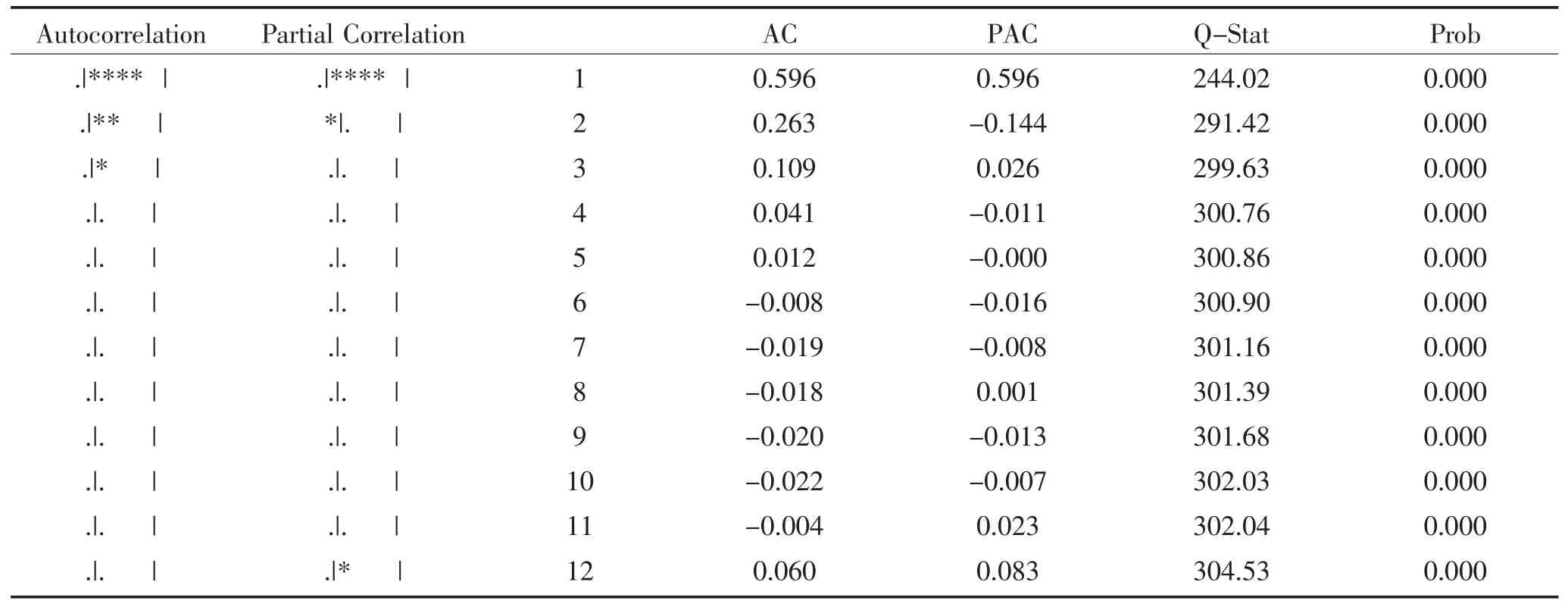
表3 方程回归残差的相关图和Q统计量Table3 Correlogram of equation of regression residuals and the Q statistic

2.3.2 ARMA模型估计

识别ARMA模型的形式后，可以使用EViews估计方程参数。模型整体上是显著的，且拟合效果良好。模型ARMA（2，1）的AIC准则和SC准则都小于ARMA（2，2）。因此认为模型ARMA（2，1）较好。

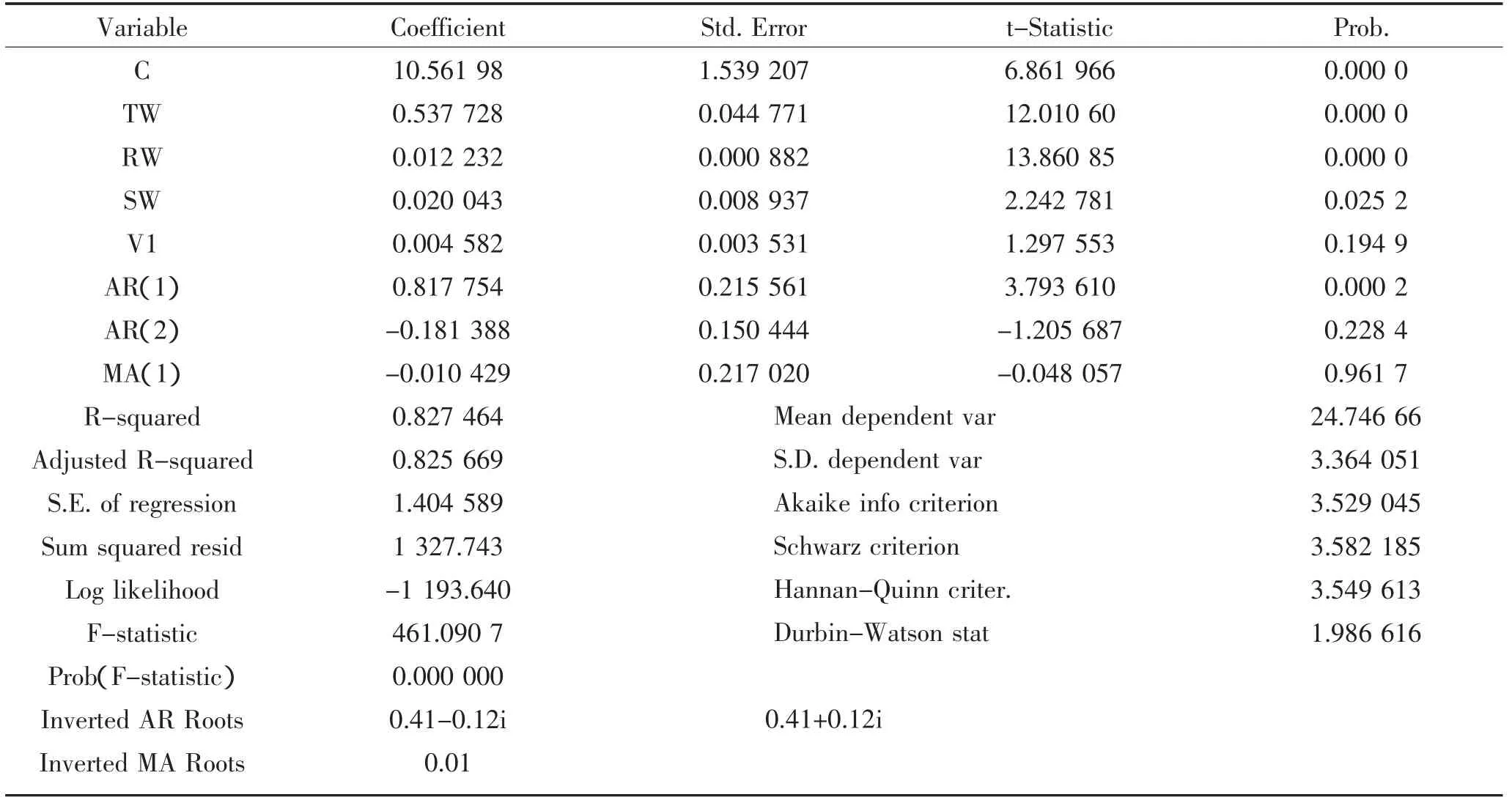
表4 ARMA（2，1）模型估计结果Table4 Results of ARMA（2，1）model estimation

利用滞后多项式写出自然通风状态下的温室室温模型ARMA（2，1）的估计结果：

（1-0.817 8L+0.181 4L2）T=10.562+0.537 7Tw+0.012 2Rw+0.02Sw+0.004 6V1+（1-0.104L）ε （9）

2.3.3 模型诊断检验

运用eviews软件包对所估计的ARMA（2，1）模型生成的残差进行自相关检验。残差序列的样本自相关函数都在95%的置信区域以内，从滞后1阶至12阶的自相关函数相应的概率值P都大于0.9，远大于检验水平0.05，因此模型ARMA（2，1）估计结果的残差序列不存在自相关。

同自然通风状态下的温室温度预测模型方法和步骤相同，建立自然通风+风机通风状态下温室室温预测模型为：

（1-0.528 7L）T=19.593 8+0.340 9Tw+0.005 3Rw+0.004 1Sw-0.002 2V2+（1-0.093 2L）ε （10）

自然通风+风机通风+湿帘降温状态下的温室室温预测模型如下:

（1-0.719 5L）T=10.935 6+0.585 5Tw+0.004 2Rw+0.006 4S-0.004 5V2+0.069 2T+（1-0.147L）ε （11）

3 模型预测与检验

根据自变量RW、TW、SW、V、TS的数据，预测三种状态下7 d的因变量温室室温T数据。取7月9日10：00-7月16日10：00的数据为已知条件进行预测数值T′与实际值T比较，部分数据如表5显示，温室温度预测值的最大绝对误差、最大相对误差、平均绝对误差和平均相对误差分别为0.9℃、4.4%、0.1℃和0.1%，三种模型均预测效果比较理想。

综上所述，预测模型通过了理论验证和实际数据检验，可以用于温室温度的预测。

表5 预测值与实际值误差表Table5 The error table of the predicted and actual value

4 结论

4.1 异常点检验和插值法对实验测量的数据修正融合，实现了温室空气温度的精确测量。

4.2 通过对模型各变量进行ADF单位根检验，表明各变量均为平稳时间序列。基于上述特征采用自相关分析，然后进行模型预估，并通过引入残差自相关检验确保模型的预测精度。

4.3 上述结果表明所建室内空气温度时间序列模型具有较高的预测精度，研究结果为全开型玻璃温室夏季的温度控制提供了良好的理论依据。

[1]李菲，李辑，管兆勇.我国东北夏季气温年代际变化特征及与太平洋海温异常关系的研究[J].气象与环境学报，2010，3（26）：19-26.

[2]李兰，王盘兴，陈长胜，等.东北夏季（6—8月）气温异常的时空特征分析[J].南京气象学院学报，2005，6（28）：801-806.

[3]李辑，龚强.东北地区夏季气温变化特征分析[J].气象与环境学报，2006，22（1）：6-10.

[4]J.J.编著.温室管理[M].郑光华，译.北京：科学出版社,1984.

[5]李文荣.论设施农业的创新与发展[J].农机化研究，2007（8）：183-186.

[6]王熙，庄卫东，汪春.黑龙江垦区农业信息化进展及展望[J].黑龙江八一农垦大学学报，2010，22（5）：18-21.

[7]Peter J Brockwel,l Richard A Davis.Time series：theory andmethods[M].New York：Springer-Verlag,1991.

[8]潘迪特SM，吴宪民.时间序列及系统分析与应用[M].北京：机械工业出版社，1988.

[9]BoxG E P.时间序列分析：预测与控制[M].顾岚,译.北京：中国统计出版社，1997.

[10]肖枝洪，郭明月.时间序列分析与SAS应用[M].武汉：武汉大学出版社，2009.

[11]H Temrati，TBoulard，A Bekkaoui．Natural ventilation and microclimatic performance of a large scale Banana Green-house[J].Journal of Agricultural Engineering Research.2001，80（3）：261-271．

[12]高铁梅．计量经济分析方法与建模[M].北京：清华大学，2004.