弧底梯形明渠正常水深的简化计算法

滕凯，周辉

（1.齐齐哈尔市水务局，齐齐哈尔161006；2.嫩江尼尔基水利水电有限责任公司）

由于弧底梯形明渠水流条件好，适宜机械化连续施工作业[1-3]，且因弧底所形成的反拱式结构，与其它断面形式比较更具有较好的抗冻性能[4-6]。因此，该种断面形式也越来越广泛地被应用于我国北方地区的水利水电供排水工程[7-8]。由于弧底梯形明渠断面正常水深计算涉及高次方程求解问题，常规的试算法、图表解法[9-11]、迭代法[12]或是计算过程繁复，或是求解成果精度不高，不便应用；而由计算机编程求解[13-16]又不便基层工程技术人员实际工作，因此，寻求一种更加简单实用的简化计算方法具有一定的实际意义，但到目前为止，尚没有比较理想的有关弧底梯形断面正常水深计算方法的研究成果。文献[17，18]通过优化拟合的方法分别给出了0＜m≤1.0、0.4≤x≤3.0和0＜m≤0.36、1.0≤x≤2.0（m为渠道坡比系数，x为无量纲水深）情况下的近似计算公式，公式适用范围小而且形式相对复杂；文献[19]通过采用级数展开形式获得了0＜m≤50、1.0≤x≤2.0情况下的简化公式，虽然公式的适用范围较大，但需计算的中间变量参数较多，计算过程繁复；文献[20]通过采用迭代法并经适当简化后获得了该种断面1.0≤m≤4.0、0.4≤x≤4.0情况下正常水深的简化近似计算式，公式的适用范围及形式稍好于其他近似公式，但因该公式涉及的中间变量参数仍显较多，适用范围仍显不够（m较小时不适用）。为了进一步改进该种断面临界水深的求解计算方法，采用优化拟合的方法，获得了计算过程简捷、求解精度高、使用范围广的简化近似计算式，可在实际工程设计中推广应用。

1 正常水深的基本计算方程

根据水力学原理[21]，正常水深的基本计算方程为：

式中：Q为渠道通过流量（m3/s）；X为湿周（m）；A为过水断面面积（m2）；n为渠道糙率；i为渠道设计坡降。

对于弧底梯形明渠（见图1所示），其正常水深计算可分两种情况：即弧底圆形断面正常水深计算（圆弧内）和弧底梯形断面正常水深计算（圆弧外）。

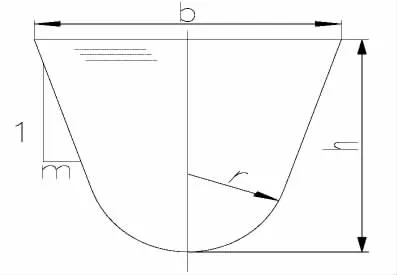
图1 弧底梯形明渠断面Fig.1 Trapezoidal cross-section with an arc bottom

1.1 正常水深计算公式判别

由断面过流条件可知，当正常水面线位于弧底曲线与梯形边坡线的切点以下时，正常水深发生在圆弧内，反之，正常水深发生在圆弧外。用数学方法可求得通过切点处的水深为：

因此可得：

当

当

其中

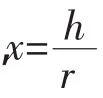
式中：h为正常水深（m）；r为弧底圆形半径（m）。

由式（2）可见，当m→∞时，h→0，切点逐步接近弧底顶点，渠道断面渐进与一条直线；而当m→0时，h→r，切点逐步接近（r，r）点，渠道断面逐步接近与标准U形明渠。

1.2 正常水深发生在弧底圆弧内时

正常水深发生在圆弧内时，实际为圆形断面正常水深计算问题，其计算公式由文献[22]可得：

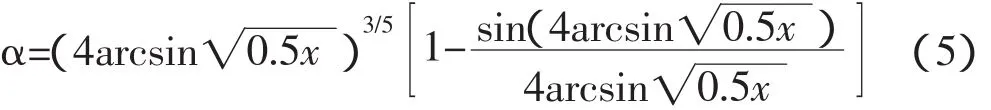
式中：α为计算参数；x为无量纲水深；θ为均匀流时的圆心角（rad）。

1.3 正常水深发生在弧底圆弧外时

正常水深发生在圆弧外时，其过水断面积及水面宽可按下式计算：

将式（6）至（8）代入式（1），并设：

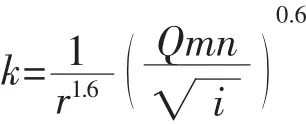
经整理即可获得求解弧底梯形断面明渠正常水深的基本计算公式为

其中，k为中间变量。

2 正常水深的近似计算公式

2.1 拟合公式的建立

式（5）及（9）为含x的高次隐函数方程，无法直接获解。为避免求解高次方程问题，在工程实用范围内[9-20]（即0.3≤m≤4.0、0.1≤x≤4.0），现假定：当正常水深发生在圆弧内及弧底圆弧外时，函数x=f（α）及可x=f（k）以分别替代式（5）及式（9）；并分别展绘x～α及x～m～k关系曲线，依据曲线关系经数值相关分析，以标准剩余差最小为目标函数[23]，即

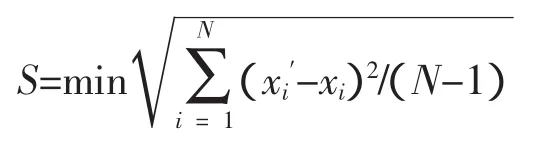
式中：N为拟合计算的数组数。

经逐次逼近拟合[24]即可获得如下替代函数，即

式中：A、B为中间变量；Q0为水面线通过弧底曲线与梯形边坡线切点情况下的渠道过流量（分界流量）（m3/s）。

Q0可由式（2）与式（10）联立求得，即为：

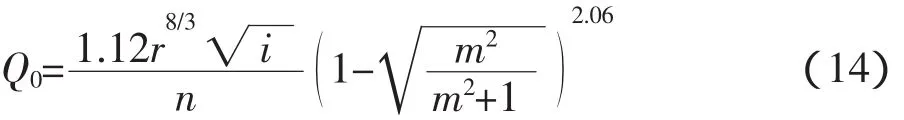
2.2 拟合公式的精度分析

为比较式（10）与式（5）、式（11）与式（9）的拟合精度，在给定的实用参数范围内，取不同的xi、mi值即可分别由式（5）及式（9）计算出与之相对应的 αi或ki，再将 αi代入式（10）、ki代入式（11）求得与之相对应的，并由下式完成拟合相对误差计算，计算结果见表1所示。

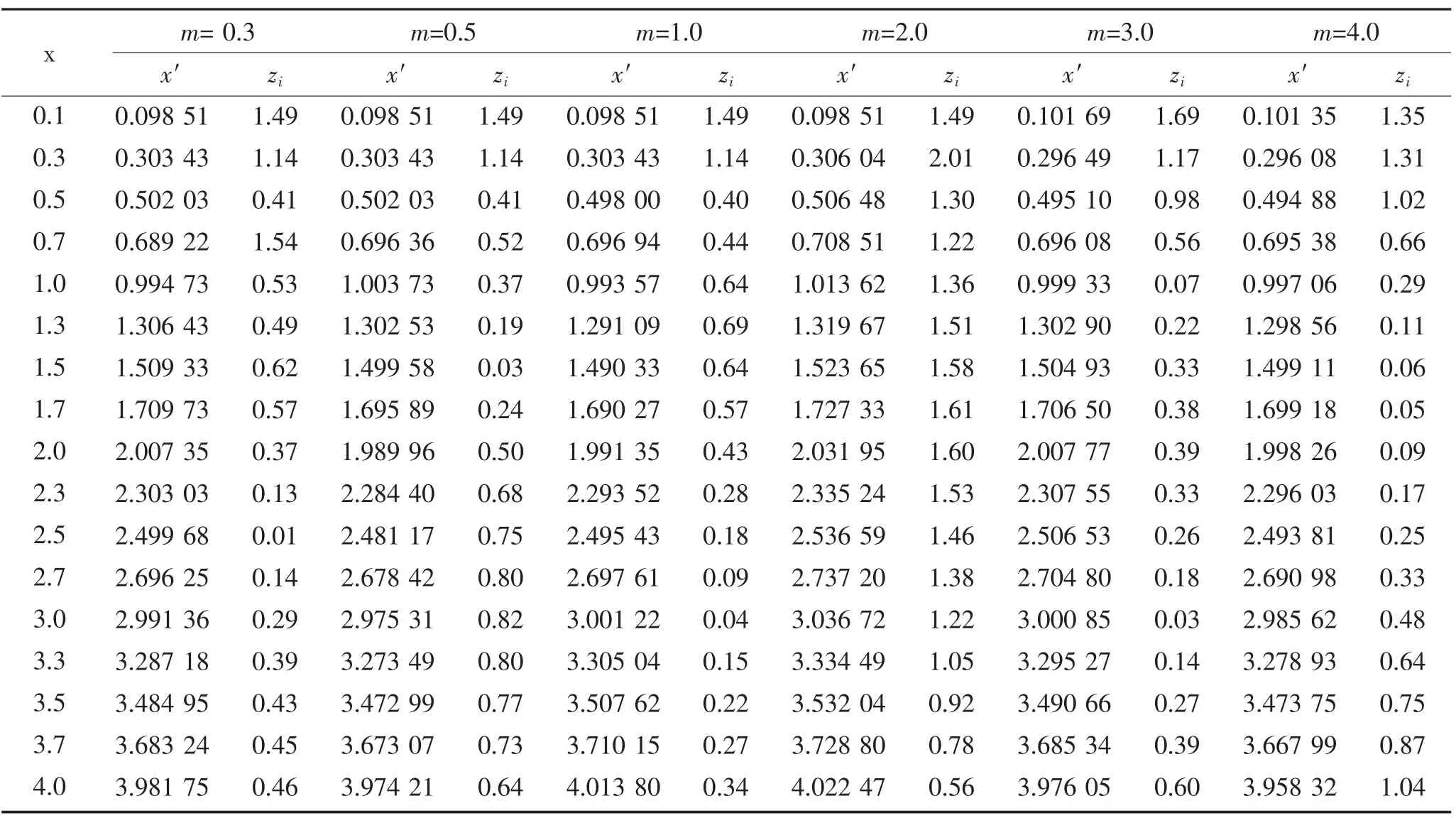
表1 式（10）、（11）拟合精度比较Table1 Type（10）,（11）fitting precision comparison

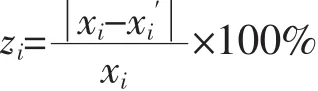
式中：zi为拟合相对误差；i为拟合计算的点数。

由表1可见，当0.3≤m＜1.0、0.1≤x≤4.0时，式中（10）、（11）的最大计算相对误差仅为1.54%。而通过对文献[20]方法计算可见，在0.3≤m＜0.5、0.1≤x≤0.329区间内，该文公式无实数解（根号下为负值）；当0.5≤m＜1.0、0.329＜x≤4.0时，公式的最大计算相对误差达到57.67%，是式中的37.45倍。当1.0≤m≤4.0、0.1≤x≤4.0时，式中（10）、（11）的最大计算相对误差为2.01%，而文献[20]的最大计算相对误差为4.65%，是式中的2.31倍。可见，式中公式具有较好的计算精度。

3 应用举例

选文献[20]算例：已知某输水渠通过流量Q=40.0m3/s，弧底半径r=2.5m，边坡比系数m=1.0，渠底坡降，糙率系数n=0.022 5，试计算渠道的正常水深h值。

解：根据已知参数可求得：

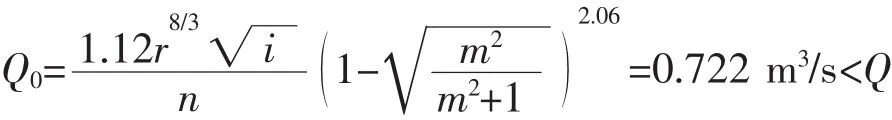
（正常水深在圆弧外）

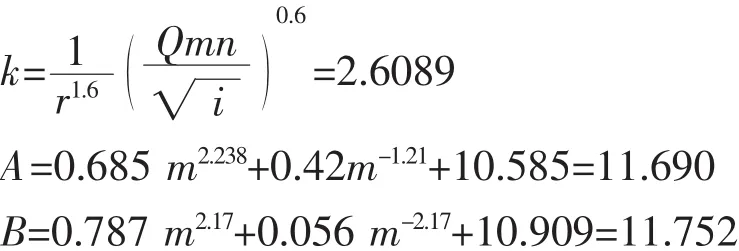
将A、B代入式（11）即可解得x为

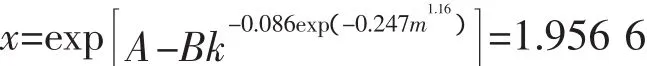
则有：h=x·r=4.892m

精确解为h=4.918 m，本文公式计算相对误差为0.5%。

4 结语

针对目前弧底梯形断面正常水深计算方法存在的问题，通过采用多参数优化拟合的方法，经逐次逼近计算，获得了表达形式相对简单且具有较高拟合精度的近似计算公式。实际工作仅借助计算器即可较简捷地完成，适于广大基层工程技术人员应用。误差分析表明，在工程实用范围内，计算相对误差不超过2.1%。通过应用举例计算分析说明，公式计算方法简捷，成果精度可靠，可在实际工程的设计中推广应用。

[1]杨彬.弧底梯形渠道全断面振捣连续滑膜衬砌机设计研究[J].陕西水利，2010（6）：91-92.

[2]王虎.不同断面形式防渗渠道的应用效果[J].防渗技术，2002（3）：31-33.

[3]李艳玲.弧底梯形混凝土衬砌渠道施工技术[J].山西水利科技，2011（1）：65-66.

[4]银俊梅.弧底梯形渠的冻胀试验研究[J].中国农村水利水电，2001（12）：140-143.

[5]王正中，李甲林，郭利霞,等.弧底梯形渠道衬砌冻胀破坏的力学模型研究[J].农业工程学报，2008,24（1）：26-31.

[6]宋玲，余书超.弧底梯形渠道受力特征及设计方法研究[J].人民黄河，2010,32（8）：128-129.

[7]冯金祥，朱勤创.弧底梯形断面在宝鸡峡灌区应用的效益[J].防渗技术，2001（2）：33-35.

[8]王文龙.弧底梯形断面在夹马口灌区续改工程中的应用[J].吉林工程技术学院学报，2004（3）：56-58.

[9]董为民，赵小利，刘卫华,等.底部含圆弧的梯形断面防渗渠道的水力计算[J].水利与建筑工程学报，2005,3（3）：54-57.

[10]刘元亮.U形渠道水力设计的一种速算法[J].陕西水利，1993（6）：21-23.

[11]谢建刚.U形渠道均匀流水深的简捷计算方法[J].湖南水利，1996（1）：14-15.

[12]吕宏兴，周维博，刘海军.U形渠道的水力特性及水力计算[J].灌溉排水学报，2004,23（4）：50-52.

[13]杨茂松，马子普.一种弧底梯形明渠临界水深的快速解法[J].吉林水利，2011（11）：21-22,23.

[14]赵晨.U形及弧底梯形渠道断面水力计算的搜索法与程序[J].水利与建筑工程学报，2006,4（3）：82-84.

[15]孙铁蕾.EXCEL在常用明渠均匀流水力计算的应用[J].水利规划与设计，2006（5）：71-72.

[16]成铁兵.弧底梯形及弧角梯形断面水力计算电算程序[J].杨凌职业技术学院学报，2008（3）：23-25，29.

[17]李风玲，文辉，黄寿生.窄深式U形渠道正常水深的近似计算公式[J].人民黄河，2006,28（12）：75-76.

[18]李风玲，文辉，陈雄.U形渠道水力计算的显式计算式[J].水利水电科技进展，2010,30（1）：65-67.

[19]滕凯，邹伟，王洪波.圆底U形渠道均匀流水深计算方法的进一步简化[J].灌溉排水，2001,20（1）：74-77.

[20]王正中，宋松柏，王世民.弧底梯形明渠正常水深的直接计算法[J].长江科学院院报，1999,16（4）：31-34.

[21]成都科学技术大学水力学教研室编.水力学[M].北京:人民教育出版社，1980.

[22]文辉，李凤玲，黄寿生.圆管明渠均匀流的新近似计算公式[J].人民黄河，2006,28（2）：67-68.

[23]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社，1999.

[24]阎凤文.测量数据处理方法[M].北京:原子能出版社，1988.