基于Cox半参数模型检测生存性状的印记数量性状位点
2012-10-16周晓晶方铭
周晓晶,方铭
(1.黑龙江八一农垦大学理学院数学系,大庆163319;2.黑龙江八一农垦大学生命科学技术学院)
印记基因是指子代中来源于亲本的等位基因仅一方亲本的基因表达,而来自另一亲本的基因表达总是受到抑制,导致该基因呈现单一来源表达的遗传现象。自从1991年印记现象被发现后[1],研究者在植物、动物及人类身上观测到了许多类似于印记的现象,随着基因印记研究的进展,陆续有学者基于区间定位方法提出了检测印记数量性状位点的遗传模型和统计方法[2-6]及贝叶斯定位方法[7-8]。
印记基因不但控制生长发育性状,也有可能控制生存性状。这类带有“右尾”偏态分布的性状常见于植物的开花期、动物的存活时间和死亡时间。目前,大多数定位数量性状位点的统计方法是在正态分布的假设下,显然不适于分析生存性状。因此,研究者将生存分析中非参数、参数及半参数的模型合并到检测生存性状位点的区间定位中[9-11]。基于加速失效模型,Cheng和Tzeng提出了参数和半参数的区间定位方法[12]。而这两种方法都涉及到误差分布的选择。采用Cox比例风险模型和偏似然函数方法的一个明显优势就是避免了选择经常令研究者“讨厌”的基线风险函数,其复杂的估计通常都比较耗时。Fang基于Cox比例风险模型,提出了在偏似然函数的框架内表征数量性状位点的方法[13],但他采用的最小二乘算法估计QTL参数,即用QTL基因型指示变量的先验概率的数学期望去估计指示变量,而这个过程中会产生“误差膨胀”。此外,如上提到的方法主要讨论以孟德尔方式遗传的QTL的相关问题[14],如QTL在基因组的位置,遗传效应、QTL之间的互作等。基因组印记现象,也被称为父母起源效应,是由每个父母基因组对后代表型的不等遗传贡献导致的。目前,还没有文献研究应用半参数方法检测生存性状的印记数量性状位点。
首先借助于Cox半参数比例风险模型构造了iQTL对生存时间的效应,此模型的好处就是不需要对性状分布做任何假设。其次,为检测iQTL,在偏似然函数的框架内,研究参数的期望最大化算法,并实现了整个基因组范围内的统计显著性的检验。最后,利用一个公开发表的老鼠模型数据集证实了此方法的统计行为。
1 方法
1.1 遗传模型
假设在给定的群体中每个位点有四个可区分的基因型,记为QMQP,QMqP,qMQP和qMqP,这里下脚标代表父母起源,观测到带有已知连锁图谱的n个个体的生存时间(T:t1,t2,L,tn),并标记基因型。假设单个QTL位于相邻的两个标记Mk和Mk+1之间,控制目标性状。基于Cox比例风险模型构造QTL对生存时间的效应,其中风险函数为

这里,λ0(tj)为基线风险函数,即当所有相互独立的变量值为零时个体的风险函数[15]。注意,如果采用参数方法时,那么就需要估计基线风险函数,但半参数方法不需要。Xj=(1 zjwjsj)为按照生存时间大小排列的第j个个体所对应的协变量值构成的向量,β=(μa d i)T为待估计系数构成的向量。zj,wj和sj分别为对应于加性效应、显性效应和印记效应的基因型指示变量,这些指示变量由Mantey等人于2005年给出[16],详细如下:

1.2 极大似然估计
记R(tj)为观测到的个体的风险集,其生存时间不小于tj,从而根据贝叶斯理论,观测到的个体的生存时间的条件概率密度为

依赖于QTL的四个基因型,记为f(tj|l),l=1,2,3,4分别对应着QTL基因型QM QP,QM qP,qM QP和qMqP。令pj|l,(l=1,2,3,4)为相应的条件概率,从而构造混合模型为

假设性状值相互独立,那么QTL参数的似然函数为n个个体上相互独立的混合模型的连乘积:

此公式称为偏似然函数[17],进一步,偏似然对数函数为:

对参数求导得:
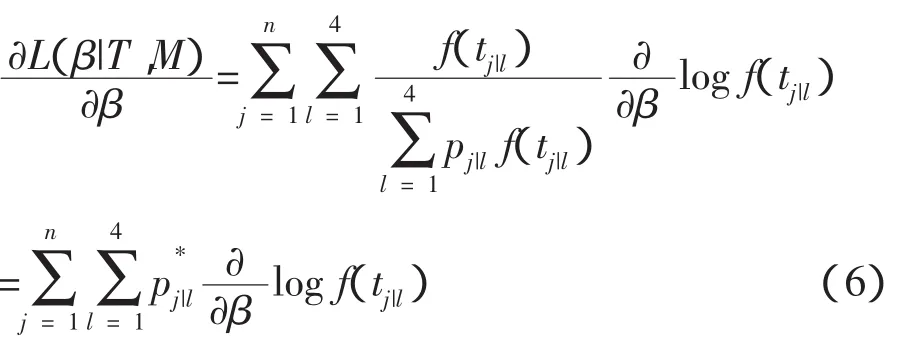

接下来,采用期望最大化算法[18]求解β的极大似然估计,迭代步骤如下:
(1)选取 β=(μa d i)T的初始值
(2)将 β(0)带入方程(7)。
(4)用 β(1)代替初始值 β(0),回到(2)继续迭代。
(5)继续迭代运算,直到结果符合设定的收敛标准为止。得到的参数值作为极大似然估计,记为
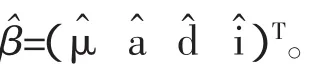
1.3 显著性检验
一般的,显著性检验步骤如下:(i)在整个基因组范围内检测QTL;(ii)确定检测到的QTL的遗传方式;(iii)鉴别印记QTL的印记类型。
具体检验过程如下:
首先,构造影响生存性状的QTL的存在性的假设

其次,当H0被拒绝时,检测到的QTL的遗传模式的假设

如果接受H0,那么检测到的QTL以孟德尔方式遗传;否则是印记的。
第三,检测到的印记QTL的印记类型取决于遗传效应a或d是否等于印记效应i,印记类型和相应的零假设参见参考文献[7]和[19]。
确定相邻两个标记区间内的显著效应处的QTL是否存在,可以通过计算零假设和备择假设构成的对数似然比检验统计量,即,这里和^1分别代表零假设H0和备择假设H1下的未知参数的极大似然估计。为实现显著性检验,采用Churchill和Doerge提出的置换检验方法[20]进行。
2 实际例子分析
我们应用提出的方法分析由高氧性急性肺损伤引发的生存时间的表观遗传属性。本研究数据集来自一个公开发表的小鼠模型系统,来源于一对互惠的近交系。其中B系(C57BL/6J)小鼠对高氧性急性肺损伤敏感,而S系小鼠对高氧性急性肺损伤具有较高的抗性。雌性B系小鼠与雄性S系小鼠交配(BS)和雌性S系小鼠与雄性B系小鼠交配(SB)产生F1代小鼠群体[21-22]。F1代小鼠间平均生存时间的差异提供了存在亲代效应的强有力的证据。F1代小鼠再采用相互交配的方式(BS×BS,BS×SB,SB×BS和SB×SB)的到4个可能的F2群体,每个群体大约产生200个个体。这些杂交个体可以用于估计潜在印记效应的遗传研究。共有840个F2代个体的生存时间(小时)表型值被测定,并且记录了分布于小鼠全基因组(包括X染色体在内)上的97个多肽微卫星标记。为了消除由于雌亲、雄亲及性别等系统环境因素对小鼠存活时间的影响,对观测数据取对数进行校正。在全基因组所有基因位点估计4种基因型的条件概率,对于有BS×BS或SB×SB的杂交方式仅得到一种杂合子,并且杂合子基因型与其亲代基因型相同,我们可以使用这种方法利用F2杂交群体估计三种可能的QTL基因型的条件概率,在给定相邻标记间的QTL基因型包括一种杂合子和两个纯合子,而且把另一种交互杂合子设置为0;对于来至BS×SB和SB×BS杂交的F2代个体,可能携带交互杂合子中的一个。假设雌雄重组率为1.25∶1.0,目的是估计那些由于缺乏可区分的交互杂合子基因型的测量标记基因型的条件概率。
检测到的iQTL的参数估计值及印记模式参见表。图描述了整个基因组范围内的对数似然比(LR)检验统计量曲线。在显著性水平为5%下经验临界值为16.7。可见,在LR图上有5个峰值超过了临界值,证实了控制小鼠急性肺损伤的生存时间的iQTL的存在性,它们分别位于1号、4号、9号、15号和17号染色体上,17号染色体的QTL以孟德尔方式遗传。
3 讨论
大多数现存的表征数量性状位点的方法是在表型值服从正态分布及完全观测到的假设条件下的,然而,这些方法不适于分析生存数据,因为这类数据通常不服从正态分布并且常带有删失数据。研究者将生存分析中的参数的、半参数的和加速失效模型合并到生存性状位点的区间定位的框架内。而这些方法主要关注以孟德尔方式遗传的QTL的检测中。在参数比例风险模型中,需要估计复杂的基线风险函数,并且涉及到如何选择最优的生存函数去拟合生存曲线。在参数的加速失效模型中,需要选择对应于生存分布的误差分布,也有可能当选择错误的误差分布时,会导致QTL的效应和位置的估计有较大的偏差。参数模型通常都会涉及到分布模型误指定问题。

表1 控制小鼠急性肺损伤的生存时间的iQTL的参数估计Table1 Parameter Estimates of survival time for acute lung injury survival time ofmice

图1 Cox半参数区间定位的LR检验统计量曲线Fig.1 The profile of LR test statistics obtained with the intervalmapping basedon Cox semi-parametricmodel for HALIsurvival time inmice
借助于Cox比例风险模型,给出了半参数的区间定位方法去表征控制生存时间的数量性状位点,此方法不需要估计基线风险函数。然后采用期望最大化算法得到印记参数的极大似然估计值,这些参数包括描述iQTL的遗传效应和印记类型。此方法成功应用于分析一个公开发表的数据集,图和表分别描述了采用本研究所给出的统计方法检测到的显著iQTL所在基因组的位置及印记性质的剖析。
[1]DeChiara,T.M.,Robertson,E.J.,&Efstratiadis,A.Parental imprinting of themouse insulin-like growth factor II gene[J].Cell,1991,64(4),849-859.
[2]Knott,S.A.,Marklund,L.,Haley,C.S.,et al.Multiple marker mapping of quantitative trait loci in a cross between outbred wild boar and large white pigs[J].Genetics1998,149(2),1069-1080.
[3]de Koning,D.J.,Rattink,A.P.,Harlizius,B.,et al.Genomewide scan for body composition in pigs reveals important role of imprinting[J].Proc Natl Acad Sci U SA,2000,97(14),7947-7950.
[4]de Koning,D.J.,Bovenhuis,H.,&van Arendonk,J.A.On the detection of imprinted quantitative trait loci in experimental crosses of outbred species[J].Genetics,2002,161(2),931-938.
[5]Tuiskula-Haavisto,M.,de Koning,D.J.,Honkatukia,M.,et al.Quantitative trait loci with parent-of-origin effects in chicken[J].Genet Res,2004,84(1),57-66.
[6]Cui,Y.,Lu,Q.,Cheverud,J.M.,et al.Model for mapping imprinted quantitative trait loci in an inbred F2 desig[J].Genomics,2006,87(4),543-551.
[7]Yang,R.,Wang,X.,Wu,Z.,et al.Bayesian model selection for characterizing genomic imprinting effects and patterns[J].Bioinformatics,2010,26(2),235-241.
[8]Hayashi,T.,&Awata,T.A Bayesian method for simultaneously detecting Mendelian and imprinted quantitative trait loci in experimental crosses of outbred species[J].Genetics,2008,178(1),527-538.
[9]Symons,R.C.,Daly,M.J.,Fridlyand,J.,et al.Multiple genetic locimodify susceptibility to plasmacytoma-related morbidity in E(mu)-v-abl transgenic mice[J].Proc Natl Acad SciUSA,2002,99(17),11299-11304.
[10]Broman,K.W.Mapping quantitative trait loci in the case of a spike in the phenotype distribution[J].Genetics,2003,163(3),1169-1175.
[11]Diao,G.,Lin,D.Y.,&Zou,F.Mapping quantitative trait loci with censored observations[J].Genetics,2004,168(3),1689-1698.
[12]Cheng,J.Y.,&Tzeng,S.Parametric and semiparametric methods for mapping quantitative trait loci[J].Computational Statistics and Data Analysis,2009,53,1843-1849.
[13]Fang,Y.A note on QTL detecting for censored traits[J].Genet Sel Evol,2006,38(2),221-229.
[14]Lander,E.S.,&Botstein,D.Mapping mendelian factors underlying quantitative traits using RFLP linkage maps[J].Genetics,1989,121(1),185-199.
[15]Kalbeisch,J.D.,&Prentice,R.L.The Statistical Analysis of Failure Time Data(Second ed.) [M].New York:Wiley,2002.
[16]Mantey,C.,Brockmann,G.A.,Kalm,E.,et al.Mapping and exclusion mapping of genomic imprinting effects in mouse F2 families[J].JHered,2005,96(4),329-338.
[17]Cox,D.R.Regression Models and Life-Tables[J].JR Statis Soc,1972,34(2),187-220.
[18]Dempster,A.P.,Laird,N.M.,&Rubin,D.B.Maximum likelihood from incomplet data via the EM algorithm[J].JR Statist Soc B,1977,39(1),1-38.
[19]Cheverud,J.M.,Hager,R.,Roseman,C.,et al.Genomic imprinting effects on adult body composition in mice[J].Proc Natl Acad SciUSA,2008,105(11),4253-4258.
[20]Churchill,G.A.,&Doerge,R.W.Empirical threshold values for quantitative trait mapping[J].Genetics,1994,138(3),963-971.
[21]Prows,D.R.,Hafertepen,A.P.,Gibbons,W.J.,et al.A genetic mouse model to investigate hyperoxic acute lung injury survival[J].Physiol Genomics,2007,30(3),262-270.
[22]Prows,D.R.,Hafertepen,A.P.,Winterberg,A.V.,et al.Genetic analysis of hyperoxic acute lung injury survival in reciprocal intercross mice[J].Physiol Genomics,2007,30(3),271-281.
