求解病态线性方程组的自动控制步长法

李雪芳，王希云

(太原科技大学应用科学学院，太原 030024)

关于病态线性方程组的求解方法有很多，主要分为直接法和迭代法。近几年出现的直接法主要有:误差转移法[1]、增广方程组法[2]等;常见的迭代法有:有残差校正迭代法[3]、Wilkinson 迭代法[4]等。

Wilkinson迭代改善是解病态线性方程组，提高解的精度的一个重要方法。杨曙光在1989年将Wilkinson迭代改善推广得到了一种定向扰动法[5];吴新元在2002年提出了步长h≡1的Wilkinson迭代法[6]来求解病态线性方程组，其迭代格式为:

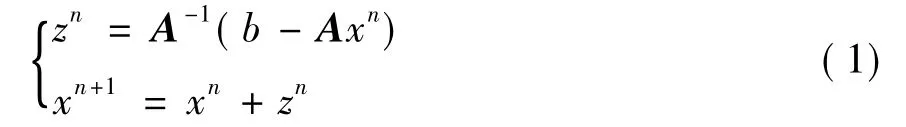
由于上述固定步长的求解方法所产生的解不是很理想，因此吴新元于2007年将一阶欧拉公式和二阶梯形法则相结合，提出了一种自动控制步长的Wilkinson 迭代法[7]，其迭代形式为:

本文在此基础上，将一阶欧拉公式和二阶R-K格式相结合，构造了一种自动控制步长的迭代格式，证明了该迭代格式的收敛性，通过数值实验结果，对所得误差做出了分析。

1 一种嵌入式的新的迭代形式

将一阶欧拉公式和二阶R-K方法结合起来，给出一种新的迭代形式。

一阶欧拉公式:

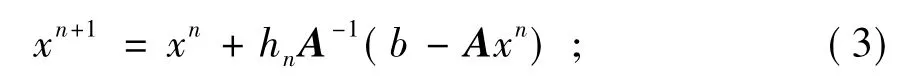
二阶R-K公式:

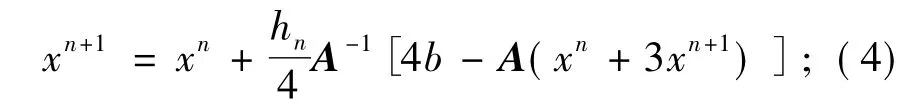
(4)式也可以等价地记为:

也就是说给定一个初始的步长，可以得到迭代形式为:

由于ˉxn+1比xn+1的阶低，因此步长h满足这样的条件:

其中ε为精度要求，h为当前步长。若s＜0.75，折半步长;若s＞1.5，加倍步长。

2 迭代形式的收敛性

如果hn=h是一个常量，则迭代形式(5)就是一个线性平稳的迭代形式，可以写成如下的形式:

其中E为单位矩阵。

此时迭代形式为:

定理1 如果hn=h＞0是一个常量，则迭代形式(8)是收敛的。

证明:很明显。如果hn=h是一个常量，且h＞0，则迭代形式(5)为迭代形式(8)，形式(8)的迭代矩阵G的谱半径为:

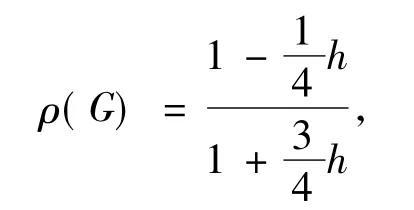
则 ρ(G) ＜ 1.

则由收敛的条件知:迭代形式(8)为收敛的。

如果hn不是一个常量，即hn是一个变量，仍可证得迭代形式(5)是收敛的。

则迭代形式(5)收敛当且仅当

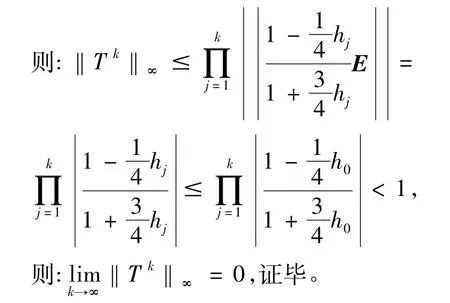
定理2说明:即使步长hn随着n的改变在变化，迭代形式(5)仍然是收敛的。

3 数值实验及分析

例1典型的病态线性方程组Ax=b，其中系数矩阵A=(aij)12×12为m ×m阶的Hilbert矩阵，

表1 例1的数值实验结果Tab.1 Numerical results of Example 1

由表1所得:在迭代次数较小的时候，已经收敛，而且迭代收敛时的误差也很小。

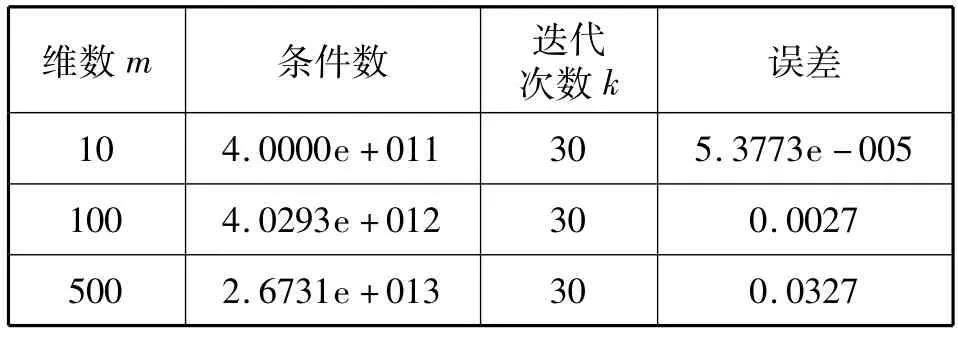
表2 例2的数值实验结果Tab.2 Numerical results of example 2

由表2所得:当矩阵维数较大时，采用该迭代格式求解，仍可得到有效的解，而且所求误差较小。

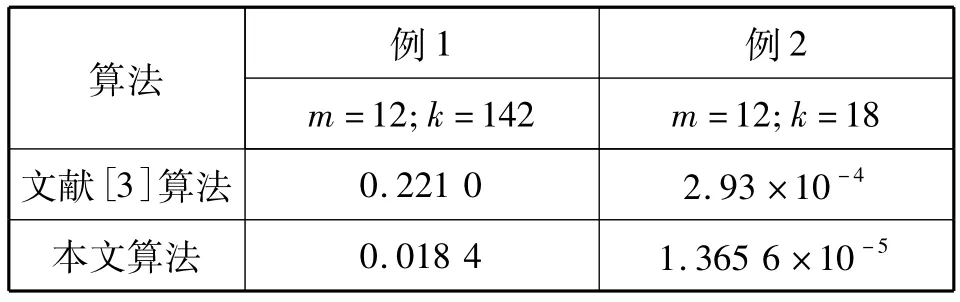
表3 数值实验结果比较Tab.3 Comparison of numerical results

由表3可得:本文所构造的迭代格式在求解病态线性方程组时，所产生的误差较小。

4 结论

本文主要在分析了Wilkinson迭代法的基础上，提出了一种自动控制步长的迭代格式，理论上证明了该迭代格式的收敛性，并通过数值实验对该迭代格式的收敛性进行了验证，而且所得解与精确解的误差非常小。因此，文中提出的算法是用来求解病态线性方程组的一个有效方法。

[1]胡胜荣，罗锡文.病态线性方程组的新解法:误差转移法[J].华南农业大学学报，2001，22(4):92-94.

[2]胡胜荣，罗锡文.病态线性方程组新解法:增广方程组法[J].华南农业大学学报，2009，30(1):119-121.

[3]颜庆津.数值分析[M].北京:北京航空航天大学出版社，1999.

[4]WILKINSON J.数字计算机上用的数字方法[M].上海:上海人民出版社，1975.

[5]杨曙光.Wilkinson迭代改善的推广—定向扰动法[J].应用数学，1989(1):37-46.

[6]WU Xinyuan，SHAO Rong，ZHU Yaran.Iterative Improvement of a solution for an Ill-Conditioned System of Linear Equations Based on a Linear Dynamic System [J].Computers and Mathematics with Applications，2002，44:1109-1116.

[7]WU Xinyuan，FANG Yonglie.Wilkinson’s iterative refinement of solution with automatic step-size control for linear system of equations[J].Applied Mathematics and Computation，2007，193:506-513.

[8]朱华，王希云.一种无约束优化问题的谱共轭梯度法[J].太原科技大学学报，2010，31(3):245-248.