带钢拉伸弯曲矫直机压弯模型的研究

刘 松，黄庆学，周存龙，窦 锋，陈 玺，徐利璞

(1.中国重型机械研究院股份公司，西安 710032;2.太原科技大学，太原 030024)

带钢拉伸弯曲矫直机可以对产品的几何精度、组织性能和表面质量进行有效的控制和提高，因而被广泛应用于精整机组、酸洗机组和镀锌机组等冷轧生产线上[1]。拉弯矫直机的辊径、辊距等结构参数是根据矫直工艺所需要的带材弯曲曲率来设计的，而且带材的弯曲曲率还直接决定了最终产品的质量。不过在实际生产中无法对带材的板形曲线和弯曲曲率进行精确测量，因而弯曲曲率的调整主要是通过对压弯量的改变来实现的[2]。

目前已有的压弯解析模型均基于材料力学中的小变形理论而且无法反映拉弯矫直过程的动态特性，因而无法准确描述压弯量和弯曲曲率间的关系。这就造成了拉弯矫直机在研发时缺乏科学的参数选取标准以及在使用时无法对产品的最终质量进行预测和控制。上述问题使得我国自主研发的拉伸弯曲矫直机在同国外进口设备的竞争中处于劣势地位。因此建立符合工程实际的压弯模型对于提高我国拉伸弯曲矫直机的市场竞争力和自主创新能力具有深远的意义。

1 带钢拉伸弯曲矫直机结构

拉伸弯曲矫直机由入、出口端的张力辊组和中间段的弯曲矫直辊组构成。张力辊组的作用是通过带钢与张力辊之间的摩擦与缠绕实现张力的放大。弯曲矫直辊组的作用是使承受着巨大张力的带材实现剧烈的反复弯曲以产生塑性延伸，从而消除带钢的三维板形缺陷。

本文的研究载体是某钢厂一弯一矫的拉弯矫直机，该矫直机由入口张力辊组、出口张力辊组、弯曲辊组和矫直辊组构成。入口张力辊组和出口张力辊组的作用是为矫直区提供巨大的张力。矫直辊组的作用是消除带材最终的残余曲率。相比于矫直辊组，弯曲辊组的辊径和辊距更小，带材在该区域发生的弯曲也更为剧烈。

为避免其他因素对带材变形曲率的影响，本文研究的是恒张力状态下延伸率为0.3%时的压弯量与带材变形曲率间的关系。

2 拉伸弯曲矫直过程的压弯力学模型

拉弯矫直过程中带材的变形基本满足工程力学中金属条材的梁弯曲理论[3-4]，根据各相关参数间的力学关系和几何关系可得

式中 δ——压弯量;

α——调整系数;

K——总变形曲率;

l—— 辊距;

式(1)反映的压弯量δ与带材弯曲曲率K间的定性关系和该矫直机在现场的使用情况基本一致。但是由于解析法基于一定的理论假设，无法计算出调整系数α的精确数值。因而该模型在使用的过程中仅起参考的作用，无法以此公式对带材的延伸率和设备承受的矫直力等参数进行精确的计算。

3 拉弯矫直过程的有限元模拟

为了排除无关附属零部件的影响并揭示拉弯矫直过程的本质和变形机理，对实际的拉弯矫直机进行了模型简化[5]。由于带材沿宽度方向的变形是对称的，因此简化后的模型为实际模型的一半，如图1所示。

图1 拉弯矫直机简化模型Fig.1 Simplified model of tension leveler

本模拟计算中所设定的摩擦系数均源自生产现场的直接反馈，如表1所示。

表1 不同接触表面间的摩擦系数Tab.1 Friction coefficients between different contact surfaces

计算完成后，将矫直区带材表层沿长度方向上的一列节点选出后，其Y向位移构成的曲线即为带材在稳定矫直过程中的弯曲状态，如图2所示[6]。

图2(a)为带材在稳定矫直过程中的Y向变形云图;图2(b)为带材在该时刻表层一列节点的纵向位移分布，即带材的板形曲线。

根据图2(b)所示的曲线进行分段拟合后由式(2)即可得到带材在该压弯量下的变形曲率。

4 拉弯矫直机压弯模型的修正和完善

将压弯力学模型的普遍适用性和有限元分析结果的精确性结合起来，利用有限元模拟的结果对压弯力学模型进行修正和完善，即可得到符合工程实际且非常精确的拉弯矫直机压弯模型。相对于矫直辊，带材在弯曲辊上的变形对产品的最终质量影响更大，因此本文仅讨论了弯曲辊的压弯量与相应的带材变形曲率间的关系，矫直辊压弯模型的研究方法与之相似。

图3为带材在不同压弯量时所对应的带材弯曲状态及其二次拟合曲线。

图2 矫直区带材的变形情况Fig.2 Deformation of strip in leveling zone

图3 不同压弯量时带材纵向位移的拟合曲线Fig.3 Fitting curves of vertical displacements of different intermeshes

表2 不同压弯量时的拟合方程和变形曲率Tab.2 Fitting equations and deformation curvatures of different intermeshes

将图3中所示的拟合方程利用式(2)计算即可得到该压弯量所对应的最大弯曲曲率，如表2所示。而且在表2中将解析法计算得到的压弯量和有限元模拟中实现的压弯量进行了对比，结果显示模拟压弯量与计算压弯量的偏差在允许的范围内，计算结果可用。将表2中的压弯量和与其对应的变形曲率进行线性拟合后即可得到二者之间的对应关系，如图4所示。

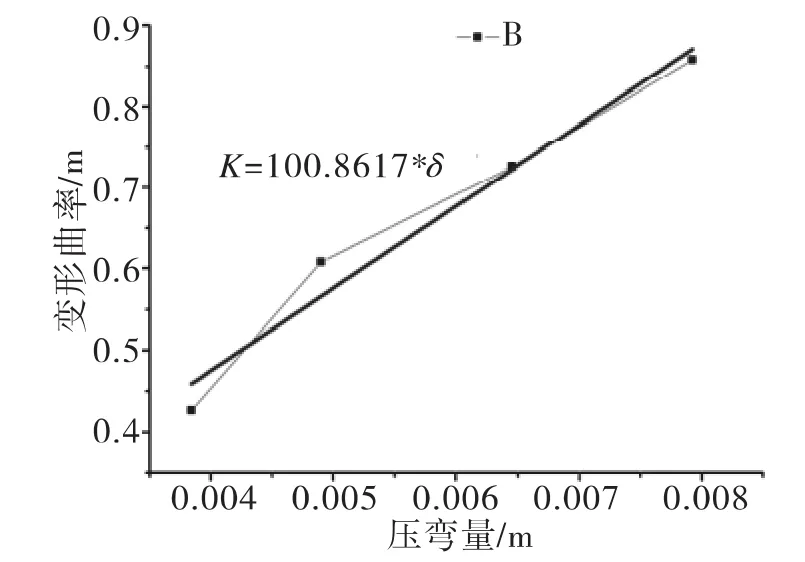
图4 变形曲率与压弯量的关系曲线Fig.4 Curve of deformation curvature and intermesh

由图4可知，该工况下带材的变形曲率与弯曲辊压弯量之间的关系为:

将式(3)和该模拟下的材质参数与几何尺寸带入到式(1)中可得，

将计算后的调整系数式(4)回代到式(1)中即可得到该弯曲单元适用于各种材质和几何尺寸的压弯量与总变形曲率的关系，由式(5)即可根据矫直工艺所要求的总变形曲率求得精确的矫直辊压弯量。

5 分析与讨论

综合利用解析法和有限元技术对带钢拉弯矫直过程的压弯力学模型进行了修正和完善，建立了较为符合工程实际的压弯模型。该模型被应用到现场后，压弯量的设定比原来基于经验的给定更为科学与精准，而且带材的矫后质量得以明显提高，事实证明该压弯模型较为符合此钢厂拉弯矫直机的实际工况。需要说明的是，该压弯模型是在恒张力状态下基于4种情况的分析和计算，因此当张力发生波动时该模型的精度会受到影响，这些情况需在现场使用中充分的考虑和避免。

[1]ZHOU CUNLONG，JIANG ZHENGYI，WANG GUODONG，et al.Deformation Work in Strip Tension Leveling[J].Advanced Materials Research，2011，145:482-487.

[2]汪建春.拉弯矫直过程中变形机理的探讨[J].武汉科技大学学报:自然科学版，2008，31(2):210-213.

[3]崔甫.矫直原理与矫直机械[M]第2版.北京:冶金工业出版社，2007.

[4]周存龙.辊式矫直过程中板带弯曲挠度的确定[J].太原科技大学学报，2009，30(1):48-50.

[5]JOHN O HALLQUIST.LS-DYNA THEORETICAL MANUAL[M].USA:Livermore Software Technology Corporation，1998.

[6]刘勇.基于ANSYS/LS-DYNA的二辊矫直过程数值模拟[J].太原科技大学学报，2011，32(2):111-116.