基于模糊随机理论的颚式破碎机齿板结构设计

闫海燕

（安徽开发矿业有限公司 六安 237462）

0 引言

目前破碎机械制造业在我国的总体规模已相当庞大，但是其发展和竞争力仍然不足，基础零部件主要还是进口，使其发展受到很大的制约。所以现今我们应该加大对破碎机基础技术和部件的研究，增强自主研发能力。

我国破碎机制造业有着非常广泛的市场前景，将应用到建筑、水利、化工、煤矿、冶金等众多行业。其中最重要是水泥行业、铺路和矿山领域的应用，其破碎机的使用占整个行业的约30%。

1 颚式破碎机齿板结构

齿板是破碎机中的重要零件，结构简单，但影响到破碎机的生产率、比能耗和破碎力等。颚式破碎机在破碎物料时齿板会直接和物料接触，会受到研磨和挤压，承受的冲击力非常大，就会产生严重的磨损，是破碎机主要的易损元件之一。因此延长齿板的寿命成为大家重视的问题。

传统的齿板设计方法是在齿板的某一点集中施力，再除以齿板的受力面积，就获得齿板受力，再研究和设计齿板的结构参数，采用这种方法忽略了齿板的载荷是不均匀分布。分析报废的齿板看出，齿板的磨损横断面上，中部的磨损最严重，两端磨损最少；纵断面上，磨损在进料口方向少，出料口方向多。同时齿板破碎力的合力点位置是变化的，因此其受力随机，我们需要仔细分析齿板的受力情况，在此基础上改进齿板的结构参数，改善颚式破碎机齿板的使用寿命。本文采用的模糊随机理论更是为这一研究提供了理论基础。

2 模糊随机理论分析

模糊随机理论结合了模糊性和随机性，它包含模糊数学、随机数学、概率论、统计学等多门学科。模糊随机理论可以求解不确定性问题和工程数据问题。模糊可靠性分析法需要准备充分的数据确定结构参数的隶属度函数。在实际情况下，并不容易得到不确定量的准确数据，需要采用如经验法、实验法等多种方法得到数据。

出现了模糊数的区间期望值视为随机集合和区间平均值，称为可能性分布。本文介绍可能性平均值、变量和协方差等的表示，研究了加权模糊数区间可能性和区间随机平均值的关系。研究表明，用随机理论可以计算模糊数线性组合的加权变量，同样可以用来确定隶属度函数值。

设基本事件是一个离散事件，基本空间表示成：

对应于基本事件的概率：

如果模糊随机事件A的隶属函数可测，其中某一元素xi属于的隶属度为mf(xi)，隶属度函数的期望值就是模糊随机事件的概率。

只要确定模糊随机事件的概率、隶属度函数和基本事件的任何两个，就能求解出第三个。本文根据经验和齿面的磨损情况来求出模糊随机事件的概率N(A)和隶属度mf(xi)。先对齿板进行模糊随机载荷法，然后再对齿板进行有限元分析、模型修改和有限元再分析。

3 齿板的受力分析

3.1 计算齿板破碎力概率分布

根据齿板的最大破碎力的作用点，把齿板分为上下部分研究，每个齿板有m个齿，将总破碎力分成上下破碎力分布概率N(B1)和N(B2)来计算。破碎力概率事件表示为：

上式中，G表示破碎力的权重函数。

N(A)归一化处理后得到N(Ai)通用表达式，即齿板破碎力的概率分布函数：

本文中假设N(BI)=1，破碎力作用点位置N(A)=0.6 ，归一化处理得到颚式破碎机的破碎力概率分布函数是：

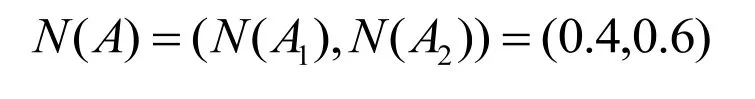
3.2 计算各齿面的破碎力

图1 齿板横向隶属度函数

本文的PE250×400颚式破碎机在获取了齿板破碎力的概率分布后，进一步计算齿板的破碎力大小：

根据实际情况，下齿板受到的破碎力最大，在有限元分析中，只计算下齿板来简化隶属度函数 m(x)的计算：mx= (ax1，ax2，!，axm)。

齿板的隶属度函数一般如图1所示。

对齿板的隶属度函数求和 ：

归一化处理求和公式后，获得齿板齿面归一化隶属度函数，还用mx表示：

图2 PE250×400动颚齿板截面示意图

解出齿板各齿面的破碎力F(x)： F' (x) = F2·mX。如图2所示为PE250×400动颚齿板截面图，该齿板有8个齿，取隶属度函数之和mm(x) = 4.6，归一化计算m (x)得：

取齿板的100mm长度进行研究，采用有限元分析齿板受力和变形，受力计算得：

4 有限元改进齿板参数结构

PE250×400颚式破碎机的齿板材料采用ZGMnl3-2，弹性模量为2.0×105MPa，泊松比为0.29，密度为7850kg/m3，屈服应力最大33lMPa。

图3为PE250×400动颚齿板的有限元应力分析结果。由图3所示，齿板的最大应力为125MPa，最小是0.26MPa。图4为齿板的有限元位移分析结果，其最大位移为3.37×10-5m，这是个相当小的尺寸，因此忽略位移情况进行分析，只研究齿板结构参数对应力在齿板分布的影响。按照材料的屈服应力和有限元分析出最大应力，计算出安全系数为2.47。齿板的应力集中在齿板的中间部位，我们各增加1个凸台，这样它就和其它三个凸台尺寸一样，再用有限元进行分析。齿板的最大应力变为37.4MPa,最小应力是0.05 MPa,明显改善了应力大小和集中，安全系数也提高到8.85。但在新加的齿板上又出现了应力集中，需要在最中间加宽为80mm，再进行有限元分析。将中间凸台加宽后最大应力的改变不大，说明我们进行的改进比较合理。

再改变齿板凸台高度来进行有限元分析，分析结果看出修改后，齿板的最大和最小应力变化不大，这表明凸台高度的变化对齿板受力影响很小，可以适当缩短齿板凸台高度结构。

可见改进齿板结构参数十分合理：改进后齿板的应力分布很大改善，但是材料基本没有增加；另外齿板安全系数明显提高，这样就能延长齿板的使用寿命，降低破碎机破碎成本。

图3 PE250×400动颚齿板应力分析结果

图4 PE250×400动颚齿板位移分析结果

5 改进齿板结构参数

在实际中设计齿板时，为了方便，通常从齿板高度的中间位置分成两部分。我们为动颚齿板进行如下修改：

将一块齿板修改为两块相同的组合齿板；凸台高度从30mm变为15mm；厚度从20mm变成15mm；在保持齿顶和齿底间距以及齿根不变，将其高度从30mm改为35mm，齿顶宽从15mm改为12mm；修改后的两块齿板重量之和减少了18.26kg，这样节约了生产和使用成本；有限元分析结果表明，修改后齿板的应力分布改善很大，应力分布也比较均匀。

6 结束语

本文针对PE250×400颚式破碎机的齿板在物料加工过程中受损严重，寿命较短的情况展开研究，采用模糊随机理论加载齿板受力状态，并计算了齿板的应力分布，进行了有限元分析。通过改变齿板结构参数，改进齿板应力分布，保证在节约材料的前提下降低了能耗，延长齿板的使用寿命，提供了可靠的理论基础。

[1]傅彩明, 饶绮麟.模糊随机理论在齿板类零件有限元仿真中的应用研究[J].湖南科技大学学报, 2006, 21(1): 33-351.

[2]张胜民.基于有限元软件ANSYS7.0的结构分析[M].北京: 清华大学出版社, 2003.

[3]Germanovich, L.N，Dyskin, A.V Fracture mechanisms and instability of openings in compression, 2000, 37(1):334-340.

[4]廖汉元, 孔建益, 钮国辉.颚式破碎机[M].北京: 机械工业出版社,2008,1-50 .

[5]孙成林.破碎机械回顾与展望[J].有色矿冶, 2005, (21):134-137.