液体火箭发动机启动段振动信号的小波去噪

杨 懿，李 薇

（北京航天试验技术研究所，北京100074）

0 引言

液体火箭发动机地面热试车是验证发动机工作性能，结构工艺可靠性的有效手段，试车过程中获得的各类数据是发动机设计、改进和定型最具有说服力的依据。发动机试车过程中采集到的振动数据中除了包含发动机自身的振动外，还包含了喷管中的高温高压燃气产生的噪声等干扰信息。尤其在点火启动段，由于发动机各组件工作的瞬态性和工作环境的骤然变化，对振动参数的测量带来极大噪声影响。因此，发动机启动段振动数据的噪声去除对还原数据的真实性有着重要作用。本文介绍基于小波分析理论的噪声去除方法，并通过真实试车数据进行了验证。

1 小波分析的基本原理

1.1 连续小波变换的基本概念

设 ψ∈L2∩L1且ψ＾（0）＝0，则按如下方式生成的函数族ψa,b｛｝

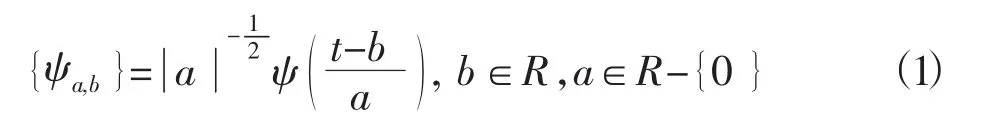
叫分析小波或连续小波。ψ叫基本小波或母小波。

设ψ是基本小波，ψa,b｛｝是式（1）定义的连续小波，则信号f∈L2的连续小波变换（CWT）定义为

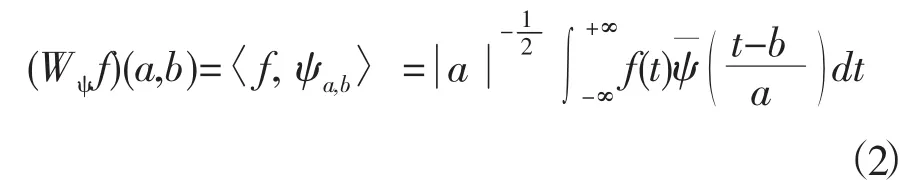
其中，“〈〉”表示内积，基本小波ψ满足如下允许性条件：

1.2 离散小波变换的基本概念

对于连续小波变换，尺度a，参数b以及时间t都是连续的。如果要利用计算机进行计算，则必须将以上参数离散化，得到离散小波变换。通常，我们把尺度a和参数b取作幂级数的形式，即

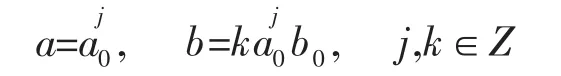
其中，a0≠1且a0＞1。对应的离散小波为

信号f(t)的离散小波变换系数为

重构公式为

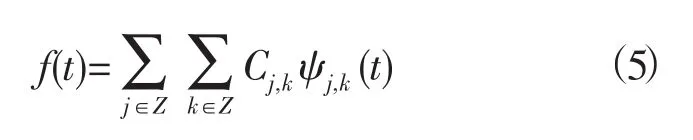
对于尺度a、参数a的离散化，通行的办法是取a0=2，b0=1。即对尺度a、参数b进行二进离散

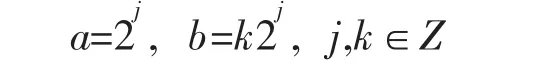
从而得到如下二进小波

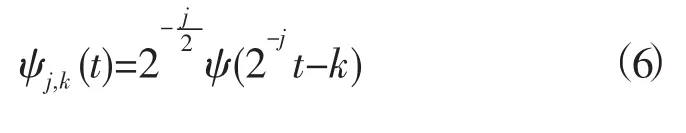
2 离散小波变换的分解、重构算法

在小波分析中，Mallat算法具有重要地位，它相当于快速傅立叶变换（FFT）在傅立叶分析中的作用。Mallat算法由小波滤波器H，G和h，g对信号进行分解和重构。分解算法如下：

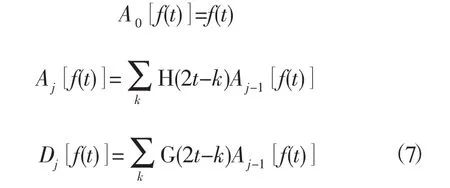
式中：t为离散时间序列号，t=1,2,3,…N；f(t)为原始信号；j为层数，j＝1,2,3,…N；j＝log2N；H，G为时域中的小波分解滤波器；Aj为信号f(t)在第j层的低频部分的小波系数；Dj为信号f(t)在第j层的高频部分的小波系数。

Mallat算法的基本思想为：对信号f(t)∈L2(R)在分辨率2j下的近似A1f进行分解，通过低通滤波器得出f(t)在分辨率2j-1下的近似Aj-1与高通滤波器得到的低频系数Dj-1。通过公式（7）的分解，将每一尺度2j上的信号f(t)分解为低频部分的小波系数Aj和高频部分的小波系数Dj。Mallat分解算法由图1表示。

小波重构则是将小波分解的过程反过来，将Mallat算法分解得到的小波系数按式（8）精确地重构出来。重构算法如下：

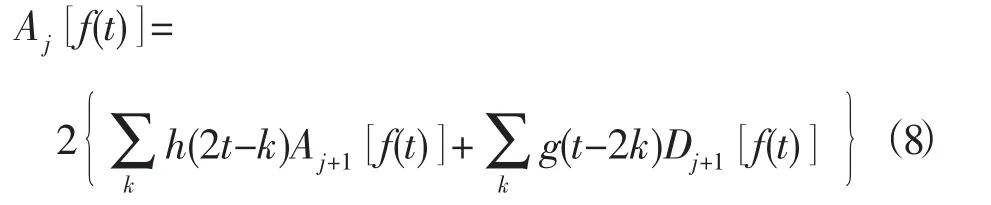
式中：j为分解层数，设J为分解的最高层数，则j=J-1，J-2，…，1，0；h，g为时域中的小波重构滤波系数。

3 发动机启动段信号的小波去噪

信号去噪的实质是去除或者抑制信号中的无用部分。对于发动机试车启动段非稳态瞬变信号的去噪，传统的傅立叶变换分析显得无能为力，而小波分析由于能同时在时频域中对信号进行分析，且具有“自动变焦”功能，所以它能有效地区分信号中的突变部分和噪声，从而实现信号消噪。

3.1 小波去噪方法

小波去噪基本方法：

1）选定小波，确定分解的层次，对信号进行一维小波分解；

2）对小波分解得到的高频系数进行阈值量化处理；

3）将小波分解得到的低频系数和高频系数进行一维小波重构。

本文采用两种不同方法，对液体火箭发动试车启动段振动信号进行去噪分析。一是默认阈值去噪处理，即利用小波函数生成的默认阈值对信号进行去噪处理。二是强制去噪处理，即将小波分解结构中的高频系数全部置零，滤掉信号中的高频部分，然后对信号进行小波重构。

3.2 试车启动段信号的小波去噪

某液体火箭发动试车启动段振动原始信号的采样速率为5 k/s，样本点数为1 024，其时域图如图2所示，频率图如图5所示。从原始信号可以看出，启动段原始数据含有大量的噪声成份。

通过对比分析各类小波的正交性、紧支性、对称性以及高阶消失矩等特点，我们选用db9小波作为小波函数，对原始信号在时域和频域上分别进行三层分解、重构，在时域上的分析结果分别如图3和图4所示，在频域上的分析结果分别如图6和图7所示。

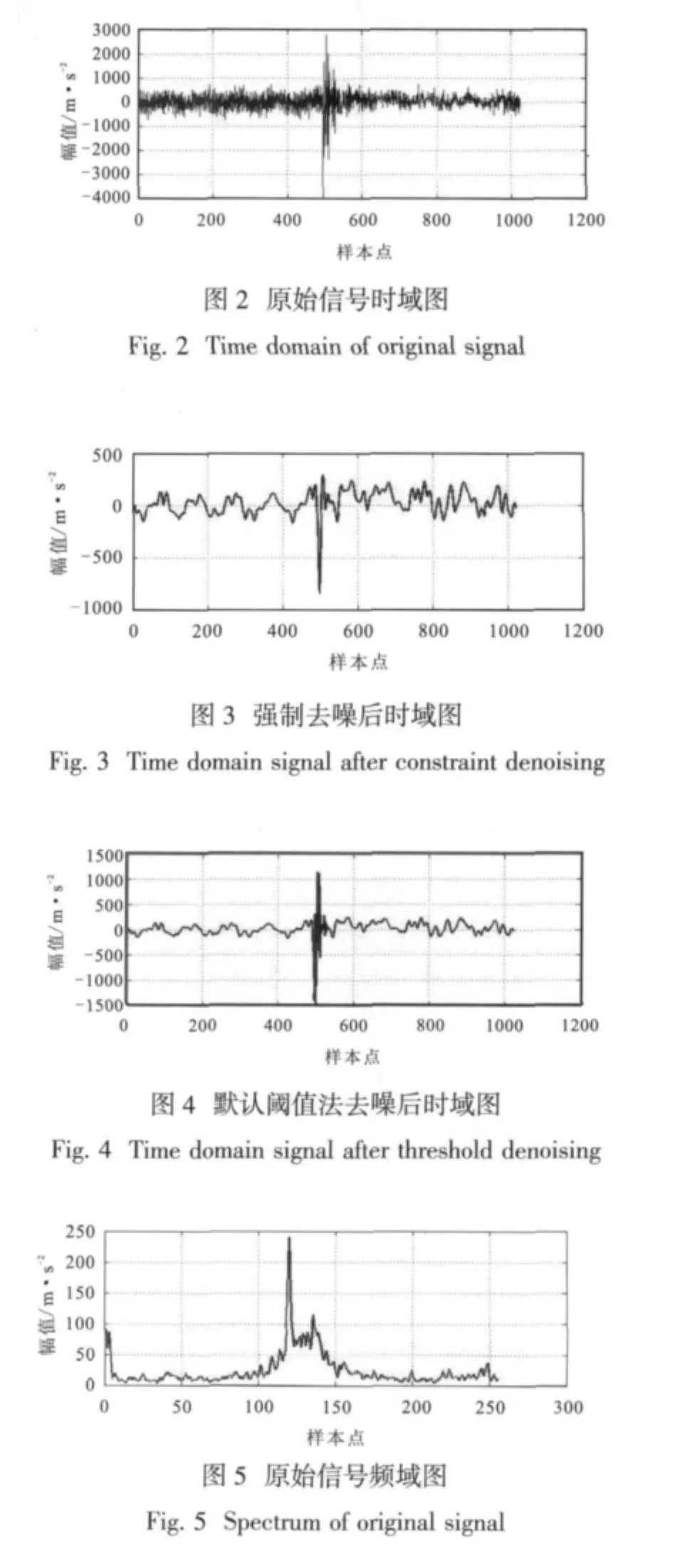
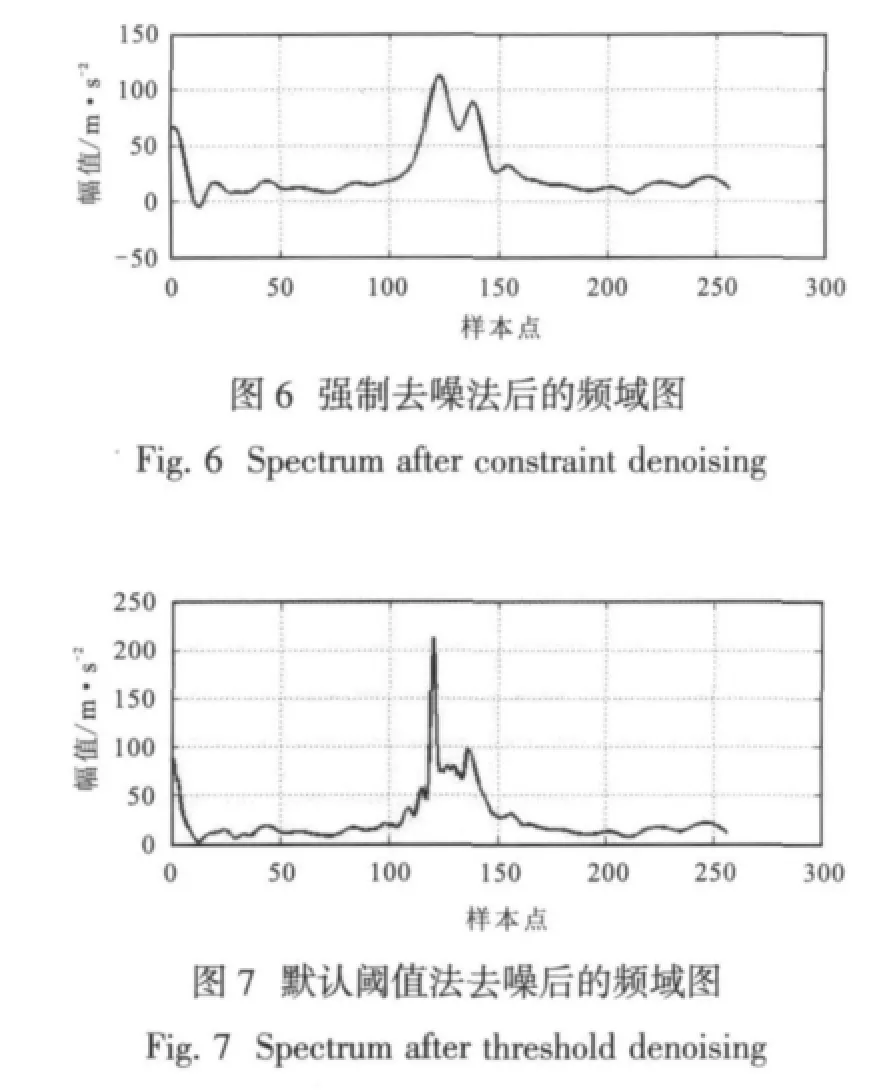
由以上分析可见：采用小波分析能对液体火箭发动机试验点火启动段的振动信号进行有效去噪处理，不同的去噪方法所得到的结果有所不同。采用强制去噪方法，由于将高频系数全部置零，丢失了部分有用的高频信息，因此去噪后的信号也比较平滑。采取阈值化去噪方法，则不会出现去噪后信号太过平滑的现象，较好地保存了原始信号中的有用信息。

对比原始信号和默认阈值法去噪后信号的时频域图可见：发动机壳体启动段振动信号经过小波去噪后，信号中的噪声成分明显减少，保留下来的有效成分也能正确反映出发动机壳体在启动段的振动信息。

4 结束语

介绍了基于小波分析理论的液体火箭发动机启动段振动信号的去噪方法，通过对实际试车启动段振动信号的处理分析，得到了良好的去噪效果。

和传统的傅立叶变换相比，小波分析在信号处理方面有着更加突出的优势。其在液体火箭发动机的试验数据分析领域的应用，还有待更深挖掘。

[1]董长虹.Matlab小波分析工具箱原理与应用 [M].北京:国防工业出版社,2004.

[2]张德丰.Matlab小波分析 [M].北京:机械工业出版社,2010.

[3]李舜酩,李香莲.振动信号的现代分析技术与应用[M].北京:国防工业出版社,2008.

[4]杨尔辅,徐用懋,张振鹏.液体火箭发动机动态数据处理的小波分析方法[J].推进技术,2001,22(2):104-107.

[5]杨雪,张振鹏,赵学军.基于小波理论的液体火箭发动机试验数据噪声处理[J].推进技术,2006,27(4):295-298.

[6]郭霄峰.液体火箭发动机试验[M].北京:中国宇航出版社,2005.

[7]王直,季娟娟,姚伟.舰船综合保障系统体系结构研究[J].电子设计工程,2011(23):50-51.

[8]朱元仿,王瑞华.改进滤波法在热管换热系统稳态检测中的应用[J].现代电子技术,2011(21):173-176.