基于弹簧阻尼模型的碰撞动力学研究

周志才，吴新跃，张文群，谢最伟

（海军工程大学机械工程学院，湖北 武汉430033）

在工程实际中，多体系统的动力学行为往往伴随着接触碰撞的发生.关于含碰撞的多体动力学建模理论，国内外在恢复系数模型、动量平衡模型和弹簧阻尼模型等适合碰撞的几种比较常用模型方面取得了诸多研究成果.弹簧阻尼模型假定变形发生在接触区的邻域，将接触模型简化为一个弹簧阻尼系统，认为碰撞过程不再是瞬时的过程，可以通过模型的数值分析计算碰撞力和作用过程［1］，能够很好地对低速碰撞问题进行模拟.本文基于等效弹簧阻尼模型对多体系统进行碰撞动力学建模研究.

1 基于能量关系的等效弹簧阻尼模型

等效弹簧阻尼法认为接触力是一种特殊的力，将碰撞过程中碰撞现象处理为连续的动力学问题，将接触力等效成一个弹簧阻尼模型（图1）.设两个物体接触点的曲率半径分别为r1和r2，接触面法线正向为n.考虑材料阻尼，广义的Hertz公式具有如下形式［2］

式中：δ为两个物体沿接触面法向相对压入型变量； δ为相对压入速度.根据 Hunt和Grossley的研究［3－4］，阻尼系数 D ＝λδn.k为弹性力学中的 Hertz刚度，它取决于材料特性和曲率半径，可表示为

式中Ei和vi分别为两个物体的弹性模量和泊松比.

图1 等效弹簧阻尼模型

1.1 滞后阻尼系数计算

将碰撞过程分为压缩阶段和恢复阶段.在压缩阶段，两个物体沿接触面法向产生形变直到两个物体的相对逼近速度为零，此时相对压缩量达到最大值δm，随后开始恢复阶段直至两个物体分离，碰撞结束.根据Hunt假设，碰撞期间的能量被阻尼耗散，式（1）表示的接触力模型相对于压入量的关系呈滞后形式（图2）.

根据能量关系确定滞后阻尼系数λ与碰撞前后的速度关系，基于Newton恢复系数e，计算碰撞期间系统的动能损耗

此外，碰撞导致的能量损耗也可沿图2所示的滞后环进行积分获得，即

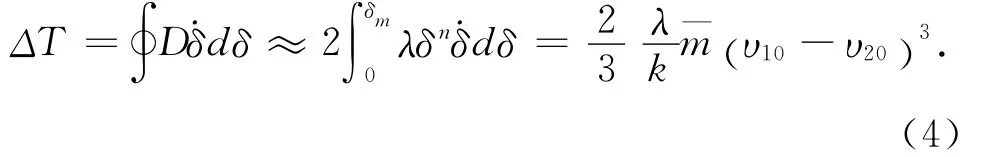
图2 Hertz接触力的滞后形式

比较式（3）和（4）可见，恢复系数和滞后阻尼系数之间满足

1.2 最大压缩量的计算

压缩阶段，两个物体的运动方程可以等价为

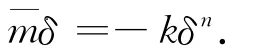
对上式进行积分，有

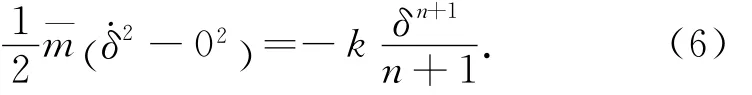
这里 δ0＝υ10－υ20.在压缩阶段结束时，相对压缩量达到最大值δm，而 δ＝0，代入式（6）可以解出

上式表明，两个物体的相对最大压缩量取决于碰撞体的质量、接触面材料性质、接触点曲率半径和碰撞前的速度.

1.3 接触时间的计算

联合式（6）和（7）可得

对上式进行积分得

当δ达到δm，即δ／δm＝1时，

假设压缩阶段和恢复阶段的接触时间相同，则可近似求得整个碰撞期间的接触时间

1.4 接触力的计算

将式（5）、（8）代入式（1）可以求得压缩阶段接触力

由于物体之间的弹性正碰撞时间很短，一般在10－3～10－5s之间，故假设恢复阶段 δ的变化与压缩阶段的变化相同［5］.压缩阶段弹簧力和阻尼力的方向相同，恢复阶段时弹簧和阻尼力方向相反，所以接触力产生滞后现象.恢复阶段的接触力可表示为

2 基于冲击函数法（impact）的弹簧阻尼模型

冲击函数法是根据impact函数来计算两个构件之间的碰撞力，其滞后阻尼系数采用step函数进行模拟.impact函数［5］的一般表达式为：

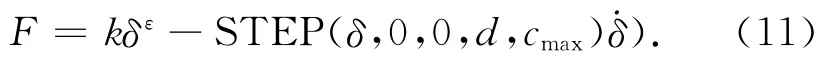
式中：ε为碰撞指数；cmax为最大阻尼系数；d为到达最大阻尼系数时的切入深度.阻尼系数形式为step（q，q0，h0，q1，h1），按下式进行计算：

对ADA MS碰撞力定义的分析表明，碰撞接触力仿真需要确定刚度系数、碰撞指数、阻尼系数和阻尼达到最大时的切入深度d.根据赫兹理论，两物体碰撞的接触刚度可根据式（2）确定；碰撞指数由式（11）可知，碰撞指数ε反映了材料的非线性程度（其推荐值金属与金属材料为1.5，橡胶材料为2）；最大阻尼系数cmax表征碰撞能量的损失，其值通常设为刚度系数的0.1%～1%；切入深度表征最大阻尼时的侵入深度，开始碰撞时没有阻尼力，随着侵入深度增大，阻尼力加大，直到最大阻尼力，其适合值为0.1 mm.

3 算例分析

以两个质量分别为m1和m2圆球物体在水平面内发生的对心正碰撞为研究算例，取两球的半径分别为r1＝25 mm，r2＝50 mm.材料取碳钢，其中弹性模量E1＝E2＝206 GPa，泊松比v1＝v2＝0.28，密度ρ＝7 800 kg／m3.初始速度υ10＝0.2 m／s，υ20＝0，分别使用基于能量关系的弹簧阻尼模型和impact函数模型对恢复系数e为0.3～0.8进行计算，得到结果如表1中所示（限于篇幅，仅列部分结果），绘制相对压入形变量与接触力曲线（图3、图4）.

表1 模型接触碰撞计算结果

图3 e＝0.8时形变接触力曲线

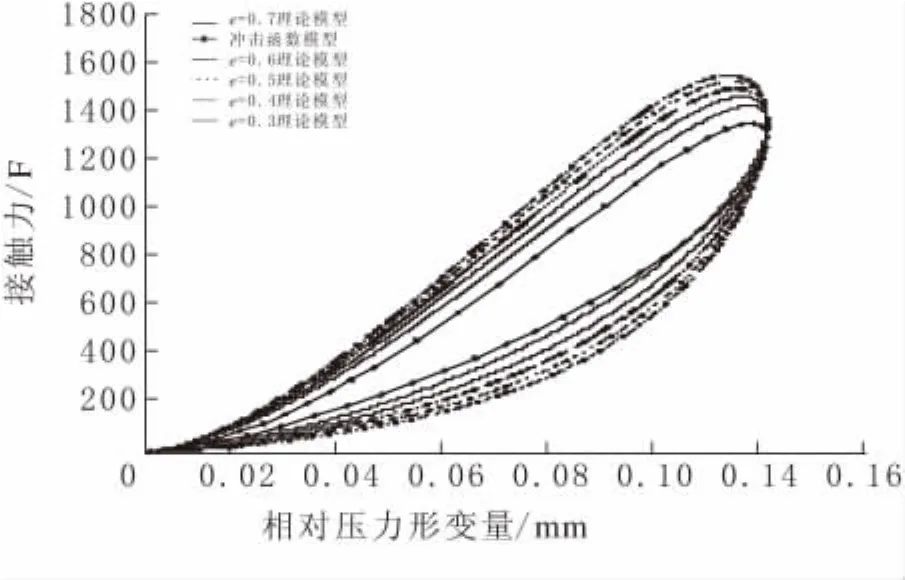
图4 e＝0.3时形变接触力曲线

由表1可以看出，当发生碰撞的两个物体的质量、接触面材料性质、接触点曲率半径和碰撞前的速度确定之后，两物体的最大形变量也就确定了，跟牛顿恢复系数无关，这与式（7）也是相吻合的；由于冲击函数模型没有考虑碰撞速度对滞后阻尼的影响，导致冲击函数模型结果仿真相比于理论计算结果存在一定误差；冲击函数模型是在恢复系数e≈1时进行模拟的，所以在恢复系数较大时冲击函数模型仿真是正确的，但当e＜0.7时，冲击函数模型的准确性比较差.

在含有接触问题的多体动力学分析中，接触模型的选取是计算结果正确与否的关键.经过以上理论计算模型和冲击函数仿真模型的对比分析，可以根据问题的特点选择合适方法，并且通过设置合理参数获得足够准确的结果.

4 结束语

本文针对碰撞模型中最常用的弹簧阻尼模型，分别进行了理论公式推导和仿真计算.将碰撞过程分为压缩阶段和恢复阶段，结合能量关系和恢复系数法对碰撞力、最大压入形变量和碰撞接触时间进行了推导，得出了显式解析解.通过ADA MS软件建立仿真模型，设置合理参数进行仿真分析，与理论计算结果进行了比较研究.理论模型的参数设置比较简单，但公式推导计算比较复杂，直观性不强；冲击函数模型直观性强，在恢复系数e＞0.7时，冲击函数模型可以得到较好的仿真结果，但是碰撞前的速度对碰撞的影响没有考虑进去，且仿真参数的设置对结果影响很大.如何正确设置碰撞参数需要更进一步的研究.

［1］丁遂亮，洪嘉振.柔性多体系统接触碰撞动力学研究［J］.上海交通大学学报，2003，37（12）：1 927－1 930.

［2］金栋平，胡海岩.碰撞振动与控制［M］.北京：科学出版社，2005.

［3］Lankarani H M，Nikravesh P E.A Contact Force Model with Hysteresis Damping for Impact Analysis of Multi－body Systems［J］.Jour nal of Mechanical Design，1990，1（12）：369－376.

［4］Lankarani H M Nikravesh P E.Continuous Contact Force Models for Impact Analysis in Multi－body Systems［J］.Nonlinear Dynamics 1994，5：193－207.

［5］李增刚.ADA MS入门详解与实例［M］.北京：国防工业出版社，2006.

［6］刘德顺，李夕兵，朱萍玉.冲击机械动力学与反演设计［M］.北京：科学出版社，2007.