线性相位FIR滤波器频域特性的教学探索

薛 健，陈后金，胡 健

(北京交通大学电子信息工程学院，北京100044)

0 引言

FIR数字滤波器是指系统单位脉冲响应h［k] 仅在有限范围内有非零值的滤波器。M阶FIR数字滤波器的系统函数H(z)可表示为

由于FIR数字滤波器很容易设计成线性相位的滤波器，在实际中FIR滤波器有着广泛的应用。

线性相位FIR滤波器的频域特性，是“数字信号处理”课程中的一个重要内容。现有的教材在分析这个问题时采用了几乎相同的方法，即利用四种线性相位FIR滤波器的时域对称特性，分别求出对应的频率响应，分析其频域特性。

本文给出了一种与传统教材不同的分析方法。该方法以Ⅰ型线性相位系统的频率响应为基础，将其他三种类型线性相位系统的频率响应表示为Ⅰ型线性相位系统的频率响应与一简单函数的乘积。该方法的特点是当Ⅰ型线性相位FIR滤波器的频率响应给出后，可以很容易地推得其他类型线性相位FIR滤波器的频率响应。由于将Ⅱ型、Ⅲ型和Ⅳ型线性相位FIR滤波器的幅度函数表示为Ⅰ型线性相位系统的幅度函数与三角函数的积，可由幅度函数表达式方便的得出不同类型线性相位FIR滤波器的频域特性。

1 线性相位条件

若M阶FIR滤波器频率响应H(ejΩ)可写为

式中，α和β是与Ω无关的常数，A(Ω)是一可正可负的实函数，则该滤波器称为广义线性相位系统，A(Ω)称为系统的幅度函数。

如果M阶FIR滤波器的单位脉冲响应h［k] 是实数，则可以证明系统是线性相位的充要条件为［1－3]

当h［k] 满足h［k] =h［M－k] ，称h［k] 为偶对称。当h［k] 满足h［k] =-h［M－k] ，称h［k] 为奇对称。由于按对称性h［k] 可分为偶对称和奇对称，按阶数h［k] 又可分为M奇数和M为偶数，所以线性相位的FIR数字滤波器有四种类型，如图1所示。

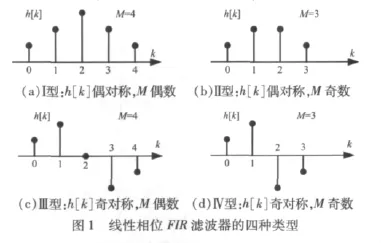
如采利用线性相位FIR滤波器的单位脉冲响应h［k] 的对称性，可得

2 线性相位系统的频域特性

四种不同类型的线性相位FIR系统，由于h［k] 的对称性及滤波器阶数M的奇偶不同，其频域特性各有其特点。

1)Ⅰ型线性相位滤波器(h［k] 偶对称，M偶数)

M阶Ⅰ型线性相位滤波器的频率响应可表示为［4-10]

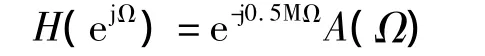
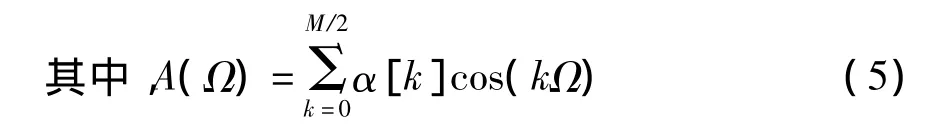
由上式知，Ⅰ型线性相位系统幅度函数A(Ω)的周期为2π，且有

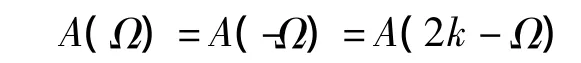
2)Ⅱ型线性相位滤波器(h［k] 偶对称，M奇数)

由系统的偶对称特性，式(4)可写为

由于M是奇数，将z=-1代入上式可得

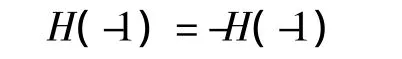
所以，H(-1)=0。故Ⅱ型线性相位滤波器可表示为

其中，H1(z)是M－1阶的Ⅰ型线性相位系统。由式(5)可知，H1(z)的频率响应可表示为

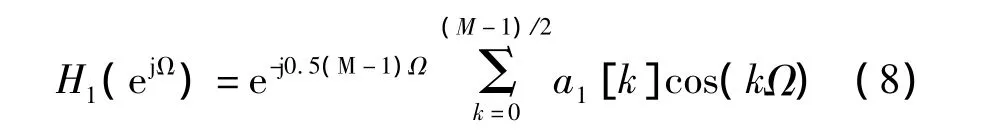
综合式(8)和式(9)，M阶Ⅱ型线性相位系统的频率响应可表示为

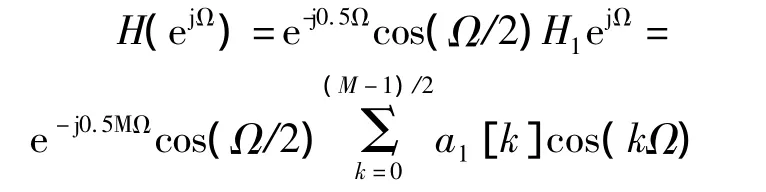
由上式可知，Ⅱ型线性相位系统幅度函数的周期为4π，且

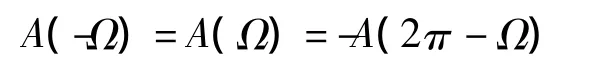
即Ⅱ型线性相位系统幅度函数A(Ω)关于Ω=0偶对称，Ω=π奇对称，并且A(π)=0。所以Ⅱ型线性相位滤波器不能用于高通和带阻等滤波器设计。

3)Ⅲ型线性相位滤波器(h［k] 奇对称，M偶数)由系统的奇对称特性，式(4)可写为

由于M是偶数，将z=-1，z=1代入上式可得

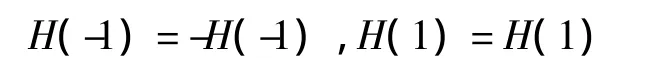
所以H(-1)=H(1)=0。故Ⅲ型线性相位滤波器可表示为

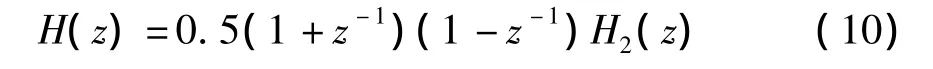
其中，H2(z)是M－2阶的Ⅰ型线性相位系统。

由式(5)和式(10)，M阶Ⅲ型线性相位系统的频率响应可表示为

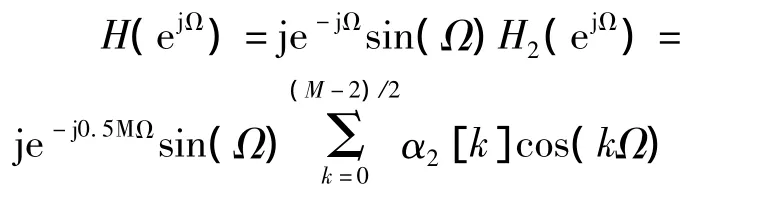
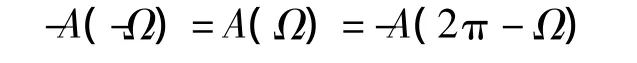
即幅度函数关于Ω=0和Ω=π奇对称，并且有A(0)=A(π)=0。所以Ⅲ型线性相位滤波器不能用于高通和低通滤波器的设计。

4)Ⅳ型线性相位滤波器(h［k] 奇对称，M奇数)

由于M是奇数，将z=1代入式(9)可得H(1)=-H(1)，所以有H(1)=0。故Ⅳ型线性相位滤波器可表示为

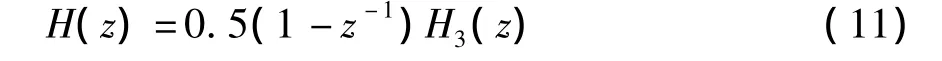
其中，H3(z)是M－1阶的Ⅰ型线性相位系统。

由式(5)和式(11)，M阶Ⅳ型线性相位系统的频率响应可表示为

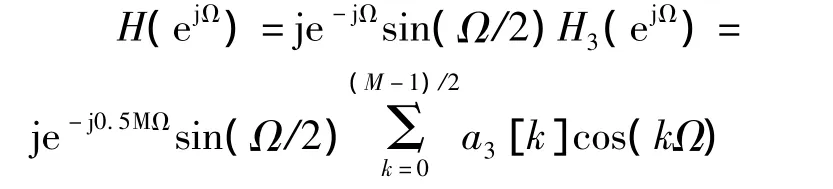
由上式可知，Ⅳ型的线性相位系统的幅度函数A(Ω)的周期为4π，且

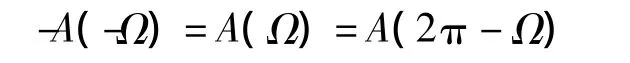
即幅度函数关于Ω=0奇对称，关于Ω=π偶对称，并且A(0)=0。所以Ⅳ型的线性相位滤波器不能用于低通滤波器的设计。

3 结语

本文给出了一种分析线性相位FIR滤波器频率响应的方法，该方法简化了线性相位FIR滤波器频率响应的分析过程，突出了FIR滤波器频域特性，便于学生掌握线性相位FIR滤波器频域特性。本文推出的幅度函数的表达式与FIR滤波器优化设计中用到的四种形式FIR滤波器的统一表示一致，但推导过程更加的简单明了，有利于课堂教学的进行和学生的理解，深受学生欢迎。

［1] S.K.Mitra，Digital Signal Processing:A Computer-Based Approach［M] .McGraw Hill，third edition，2006

［2] John.Proakis，Digital Signal Processing:Principles，Algorithms and Application［M] ，fourth edition，Prentice Hall，2007

［3] 黄建国，刘树棠译，离散时间信号处理［M] ，北京:科学出版社，1998年

［4] 胡广书，数字信号处理［M] ，第2版，北京:清华大学出版社，2003

［5] 程佩青，数字信号处理教程［M] ，第3版，北京:清华大学出版社，2007

［6] 高西全，丁玉美，阔永红，数字信号处理［M] ，第2版，北京:电子工业出版社，2010

［7] 吴镇扬，数字信号处理［M] ，第2版，北京:高等教育出版社，2010

［8] 姚天任，江太辉，数字信号处理［M] ，第3版，武汉:华中科技大学出版社，2007

［9] 郑南宁，程洪，数字信号处理［M] ，北京:清华大学出版社，2007

［10] 陈后金，薛健，胡健，数字信号处理［M] ，北京:高等教育出版社，2008